研究者对长期吸烟的人进行戒烟干预,三种干预措施分别为:① hypnotherapy programme – 催眠疗法;② nicotine patches – 尼古丁贴片;③ e-cigarettes – 电子烟。
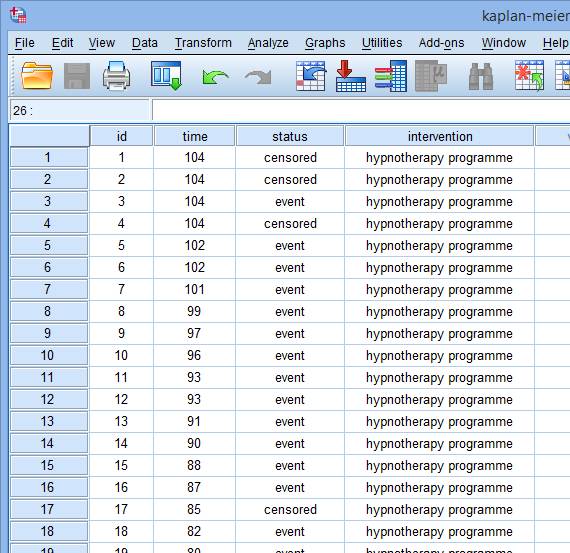
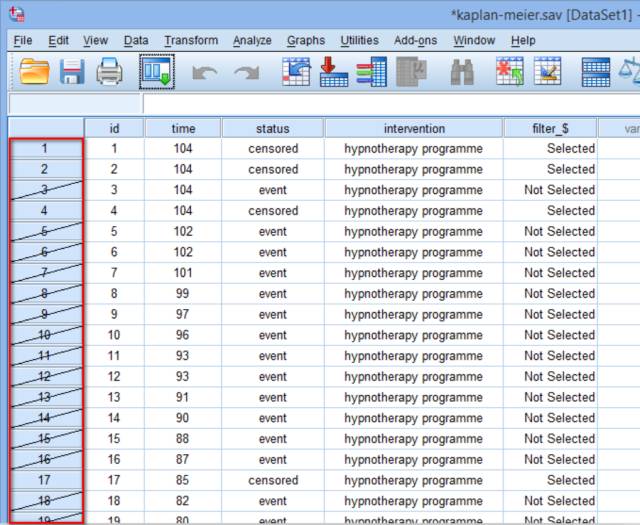
研究纳入了150例长期吸烟者,随机分配到三个干预组中,每组各50例研究对象。研究的起始时间是吸烟者戒烟后,研究持续2年(104周)。结局是“再次吸烟”或“未再次吸烟”。
通过 Kaplan-Meier生存分析方法可以实现以下两个目标:
1. 三个干预组的“生存”分布是否不同;
2. 如果三个干预组的“生存”分布存在差异,具体是哪两种干预措施之间存在差异。
研究者收集了150例受试者的“生存”时间(time,单位:周)、结局(status:censored – 截尾,用“0”表示;event – 再次吸烟,用“1”表示)和干预措施(intervention:hypnotherapy programme – 催眠疗法,用“1”表示;nicotine patches – 尼古丁贴片,用“2”表示; e-cigarettes – 电子烟,用“3”表示),部分数据如下:
(注:这里status和intervention显示的是变量值标签而非数值,可以通过在菜单栏上选择View > Value Labels来实现。)
使用Kaplan-Meier法进行生存分析时,需要考虑6个假设。
对研究设计的假设:
假设1:结局变量是二分类变量,分别为“截尾”和“事件”;
假设2:研究的起始和终止时间(也称“生存时间”)需要明确定义并测量;
假设3:尽量减少左截尾事件,所谓左截尾,是指观察的起始时间难以确定。比如,研究皮肤癌患者的生存时间,理想的起始时间是皮肤癌发生的一刻,但一般情况都是患者被诊断时作为起始时间,这样观察的时间就不能代表皮肤癌发生到死亡的真正生存时间,所以要尽量要避免左截尾的发生;
假设4:“截尾”和“事件”相互独立,如事件是死亡,那么截尾不能是死亡或与死亡相关的情况;
假设5:不应该有长期变异。一般试验的开始到结束的时间较长,而纳入的研究对象是经过一段时间收集的,并不是同时进入研究。如研究皮肤癌发生到死亡的生存时间,如果在试验的时间内出现了新的药物,提高了后期进入试验研究对象的生存率,这样的“变异”就会对研究结果造成偏倚。
对数据的假设:
假设6:截尾在各个组的比例和分布相似。
那么,进行Kaplan-Meier分析时,如何考虑和处理这6个假设呢?
由于假设1-5都是对研究设计的假设,需要研究者根据研究设计进行判断,所以本文主要对数据的假设6进行检验。假设6包括两个方面:截尾在各个组的比例相似;截尾在各个组的分布相似。
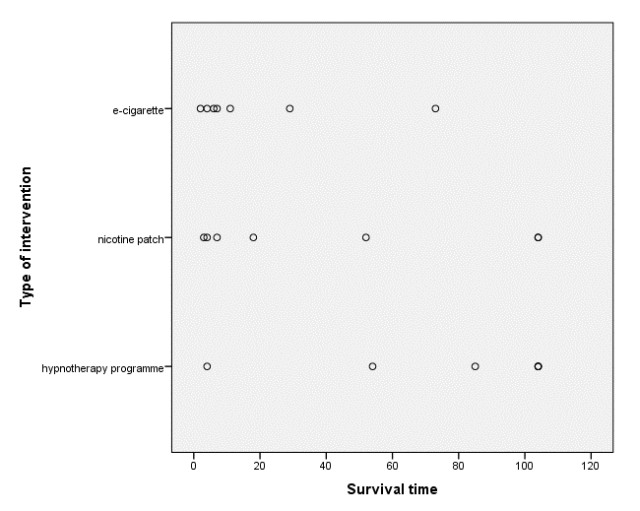
我们先通过散点图对截尾的分布进行判断。
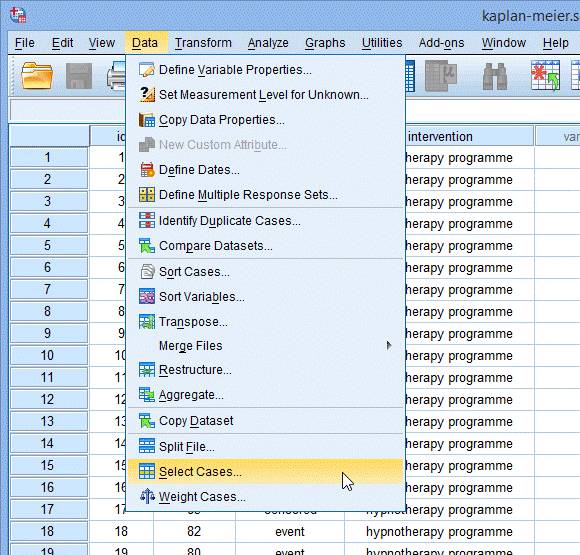
1. 首先要选出“截尾”的数据,在主菜单点击 Data > Select Cases... ,如下图:
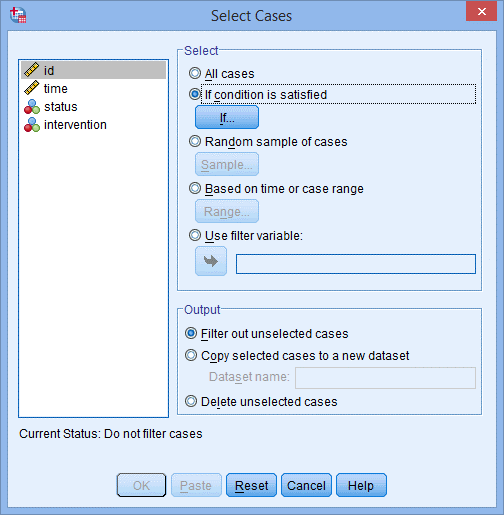
2. 选择If condition is satisfied,点击If。
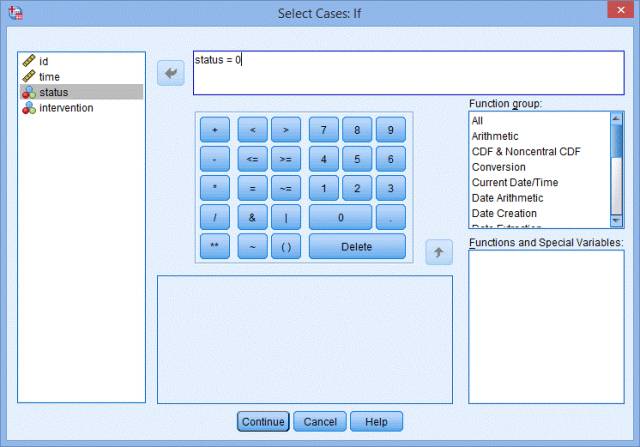
3. 将status=0填入右上方的方框内,点击Continue,点击OK。
4. 打开变量视图,可以看到status为event的数据已被过滤掉。
5. 做散点图
(1) 在主菜单点击 Graphs > Chart Builder...,如下图所示:
(2) 在Chart Builder对话框下,从Choose from选择Scatter/Dot,在中下部的8种图形中,选择左上角的那一种(如果点击这个图标会出现“Simple Scatter”字样),并拖拽到主对话框中。
(3) 主对话框中会出现标记“Y-Axis?”和“X-Axis?”的方框,将time拖拽到“X-Axis?”,intervention拖拽到“Y-Axis?”,点击OK。
(4) 从下图可以看到,截尾随时间均衡分布(尽管电子烟和尼古丁贴片在生存时间较小时有些聚集)。由于截尾在各个组的分布是否相似没有一个严格的检验方法和标准,我们这里认为截尾在三个干预组中分布相似。
(5) 下面对刚才选择的数据去过滤:在主菜单点击 Data > Select Cases... ,如下图所示。
(6) 选择All cases,点击OK。
(7) 在变量视图中可以看到所有的数据都被选择,如下图。
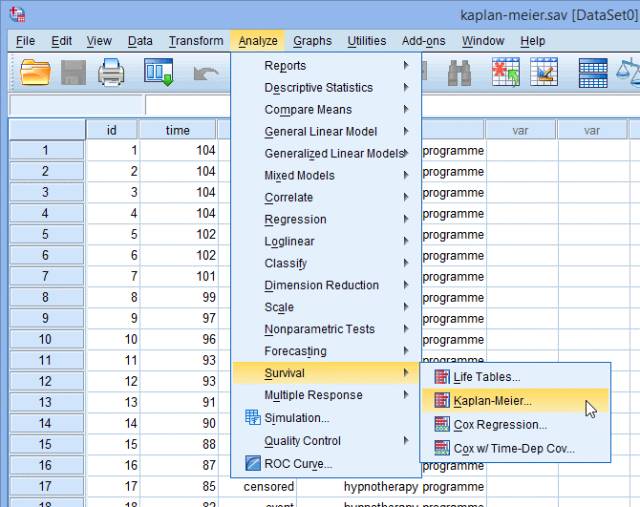
1. 在主菜单点击Analyze > Survival > Kaplan-Meier... ,如下图:
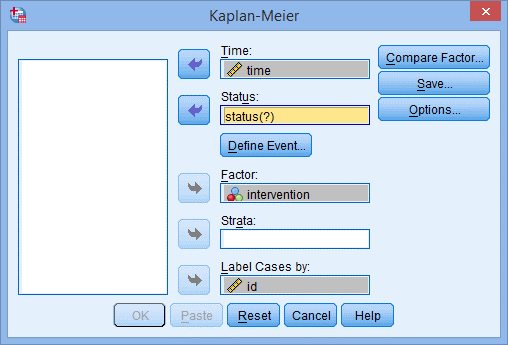
2. 将time选入Time,将intervention选入Factor,将id选入Label Cases by,将status选入Status,点击Define Event。
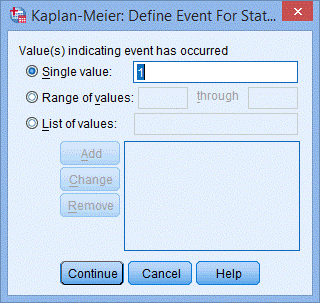
3. 本研究中status=1代表事件,即再次吸烟,所以在Single value中填入1。
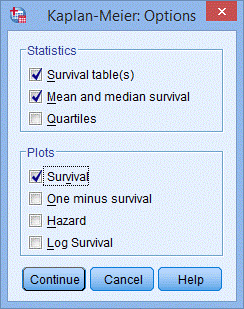
4. 点击Options,选择Statistics下面的Survival table(s)和Mean and median survival, 选择Plots下面的Survival,点击Continue。
5. 点击Compare Factor,选择Test Statistics下的Log rank、Breslow和Tarone-Ware,点击Continue,点击OK。
6. 由于上面的检验是对三个组的分布进行的检验,如果想知道每两个组之间的差异是否存在,就需要进行两两比较。进行两两比较时,重新进行上述操作1-5,在Compare Factor Levels时,选择Test Statistics下的Log rank,下方选择Pairwise over strata,点击OK。
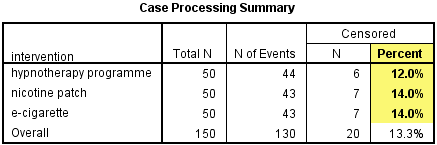
1. 在Case Processing Summary的表格中,我们可以看到截尾在催眠疗法、尼古丁贴片和电子烟三个组中所占的比例分别是12.0%、14.0%和14.0%,较为相似,验证了我们假设6“截尾在各个组所占比例相似”。
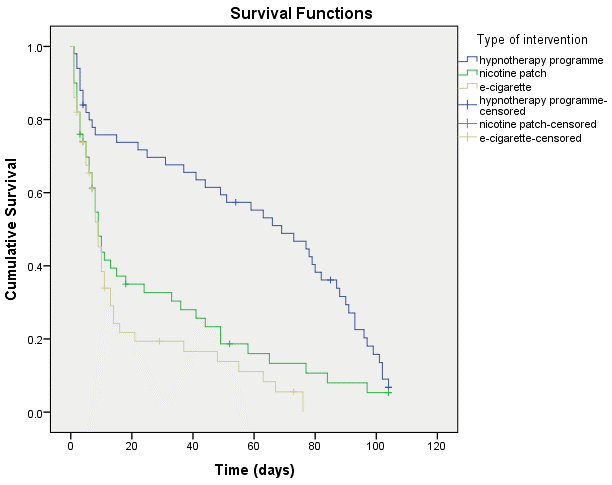
2. 三种干预措施的生存曲线如下图所示,我们可以大致看出催眠疗法的“生存”时间比尼古丁贴片或电子烟长。
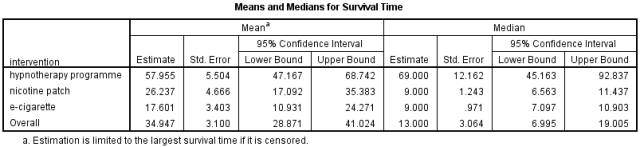
3. 在Means and Medians for Survival Time表格中,可以看到三种干预措施的“生存”时间和总“生存”时间的均值和中位数及相关统计量。由于“生存”时间一般不符合正态分布,所以这里均值没有中位数的意义大。
催眠疗法、尼古丁贴片和电子烟三个组的“生存”时间中位数分别是69.000(95%CI:45.163-92.837)周、9.000(95%CI:6.563-11.437)周和9.000(95%CI:7.097-10.903)周。催眠疗法的“生存”时间比另外两种干预措施长,验证了我们在“生存”曲线看到的情况。
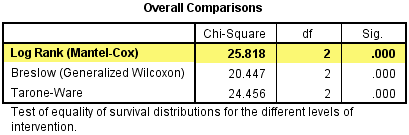
4. 在Overall Comparisons中,我们分别用了Log rank test (Mantel, 1966), Breslow test (Breslow, 1970; Gehan, 1965) 和Tarone-Ware test (Tarone & Ware, 1977)。
一般情况下,三种检验都勾选,如果三种检验的结果一致(P均小于0.05或均大于0.05),则报告Log rank检验的结果;如果三种检验结果不一致,则需要检查截尾数据在各个组的分布情况并进一步讨论。三种方法均采用的是卡方检验。
本例中,三种方法的P值均小于0.001,所以报告Log rank检验的结果:三个干预组中“生存”分布的差异具有统计学意义,χ2= 25.818,P<0.001。
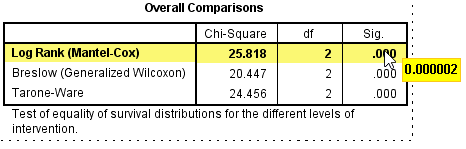
这里我们看到P值显示为0.000,这并不代表P=0.000,如果想知道具体的数值,可以双击表格,并将鼠标移动至0.000处,会显示真正的P值,为0.000002,已经在下图中突出显示。
5. 在Pairwise Comparisons表格中,我们可以看到通过Log rank方法检验的两两比较的结果。与多组比较相同,两两比较也是计算卡方统计量。但两两比较是进行了多次,所以显著性水平P值不再是0.05,需要用Bonferroni法校正。
该两两比较共进行了三次:催眠疗法与尼古丁贴片,催眠疗法与电子烟,尼古丁贴片与电子烟。所以校正后的显著性水平=0.05/3≈0.0167,即当表格中P<0.0167时,认为差异有统计学意义。
(1) 催眠疗法与尼古丁贴片:催眠疗法组与尼古丁贴片组的“生存”分布的差异具有统计学意义,χ2 =11.035,P<0.001。见下图突出显示的部分。
(2) 催眠疗法与电子烟:催眠疗法组与电子烟组的“生存”分布的差异具有统计学意义,χ2 =29.003,P<0.001。见下图突出显示的部分。
(3) 尼古丁贴片与电子烟:尼古丁贴片组与电子烟组的“生存”分布的差异不具有统计学意义,χ2 =1.541,P=0.214>0.0167。见下图突出显示的部分。
本研究将吸烟者随机分配到三个干预组中:催眠疗法组(n=50),尼古丁贴片组(n=50)和电子烟组(n=50)。运用Kaplan-Meier生存分析比较三种干预措施对戒烟的效果。截尾在三个组所占的比例相似,催眠疗法组、尼古丁贴片组和电子烟组分别是12.0%、14.0%和14.0%,截尾在各个组的分布也相似。
催眠疗法组戒烟后再吸烟的中位时间为69.0(95%CI:45.2-92.8)周,比尼古丁贴片组(中位时间:9.0周,95%CI:6.6-11.4)和电子烟组再次吸烟(中位时间:9.0周,95%CI:7.1-10.9)的中位时间长。用Log rank法对三种干预措施的“生存”分布的差异进行检验。三个干预组中“生存”分布的差异具有统计学意义,χ2 = 25.818,P<0.001。
运用Log rank法对三种干预措施进行两两比较,并对显著性水平进行Bonferroni校正,校正后的显著性水平为≈0.0167。催眠疗法组与尼古丁贴片组的“生存”分布的差异具有统计学意义,χ2 =11.035,P<0.001;催眠疗法组与电子烟组的“生存”分布的差异具有统计学意义,χ2 =29.003,P<0.001;然而,尼古丁贴片组与电子烟组的“生存”分布的差异不具有统计学意义,χ2 =1.541,P=0.214。