1、分析原理
协方差分析是回归分析与方差分析的结合。在作两组和多组均数之间的比较前,用直线回归的方法找出各组因变量Y与协变量X之间的数量关系,求得在假定X相等时的修正均数,然后用方差分析比较修正均数之间的差别。
要求X与Y的线性关系在各组均成立,且在各组间回归系数近似相等,即回归直线平行;X的取值范围不宜过大,否则修正均数的差值在回归直线的延长线上,不能确定是否仍然满足平行性和线性关系的条件,协方差分析的结论可能不正确。
对于协变量的概念,可以简单的理解为连续变量,多数情况下,连续变量都要作为协变量处理。
2、问题
欲了解成年人体重正常者与超重者的血清胆固醇是否不同。而胆固醇含量与年龄有关,资料见下表。
| 正常组 | 超重组 | ||
| 年龄 | 胆固醇 | 年龄 | 胆固醇 |
| 48 | 3.5 | 58 | 7.3 |
| 33 | 4.6 | 41 | 4.7 |
| 51 | 5.8 | 71 | 8.4 |
| 43 | 5.8 | 76 | 8.8 |
| 44 | 4.9 | 49 | 5.1 |
| 63 | 8.7 | 33 | 4.9 |
| 49 | 3.6 | 54 | 6.7 |
| 42 | 5.5 | 65 | 6.4 |
| 40 | 4.9 | 39 | 6.0 |
| 47 | 5.1 | 52 | 7.5 |
| 41 | 4.1 | 45 | 6.4 |
| 41 | 4.6 | 58 | 6.8 |
| 56 | 5.1 | 67 | 9.2 |
3、统计分析
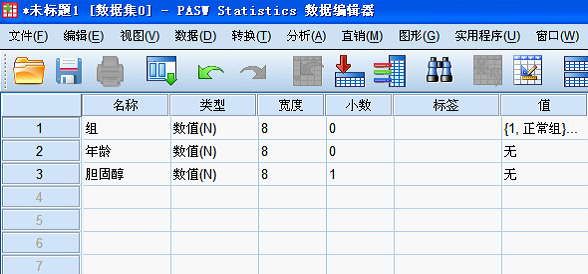
(1) 建立数据文件
变量视图:建立3个变量
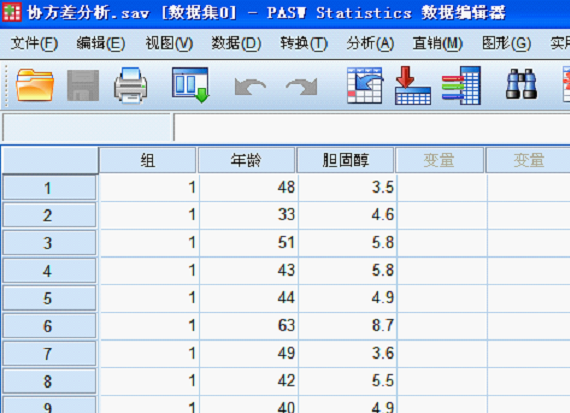
数据视图:
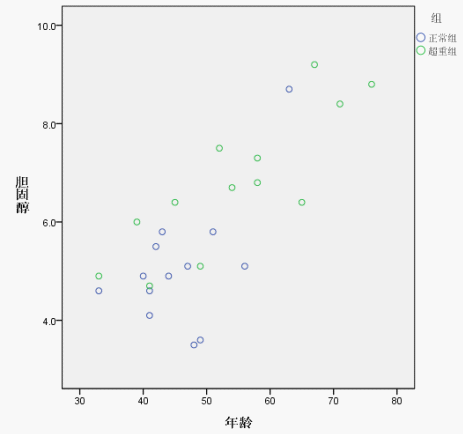
先要分析两组中年龄与胆固醇是否有线性关系,且比较回归洗漱是否相等,比较粗略的做法是画散点图,选择菜单:图形 -》旧对话框 -》散点图,如图:
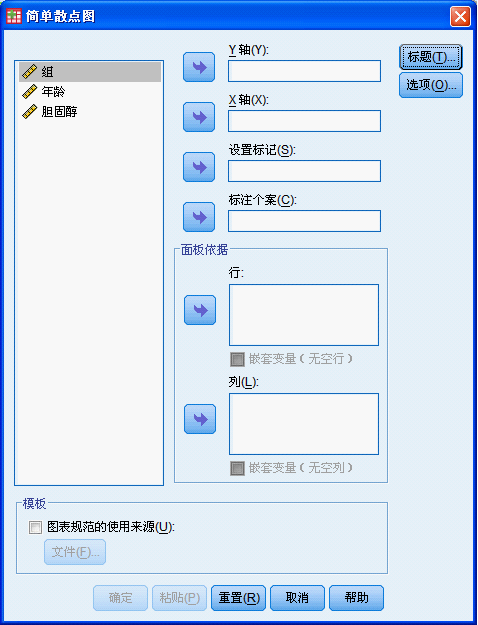
进入图形对话框:
将胆固醇、年龄、组分别选入Y轴、X轴、设置标记:
点击确定开始画图
可以看出,大致呈直线关系。
更为精确的作法是检验年龄与分组之间是否存在交互作用,即年龄的作用是否受分组的影响。
接下来开始协方差分析,首先进入菜单:
进入对话框
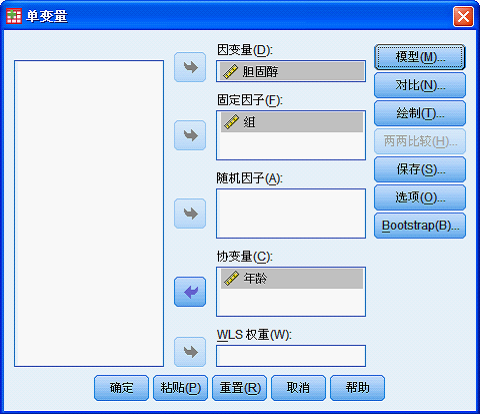
将胆固醇选入“因变量”,组选入“固定因子”,年龄选入“协变量”,见图:
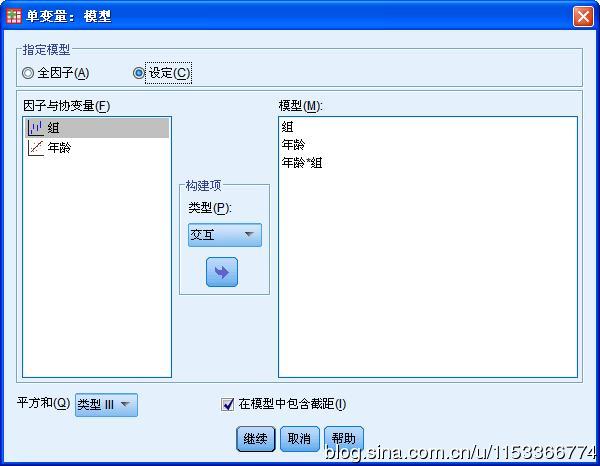
点击右边“模型”按钮,在“构建项”下拉菜单中选择“主效应”,将“组”和“年龄”选入右边框中,然后在“构建项”下拉菜单中选择“交互”,同时选中“组”和“年龄”,一并选入右边的框中,见图:
点击“继续”按钮回到“单变量”主界面:
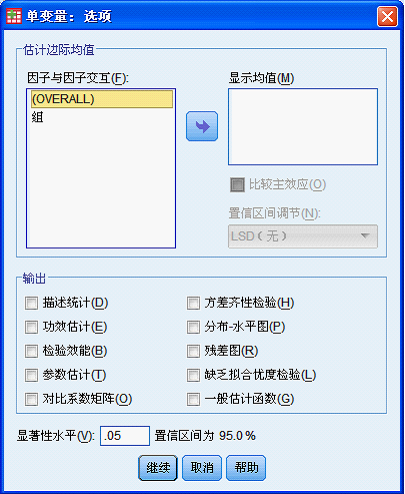
单击“选项”按钮,进入如下对话框:
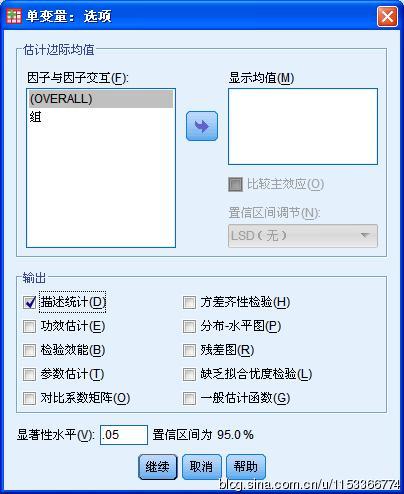
选中“描述性分析”:
点击“继续”按钮回到主界面,单击“确定”即可。
4、结果解读
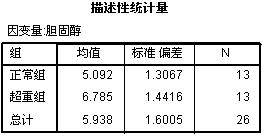
这是各组的描述性统计分析。
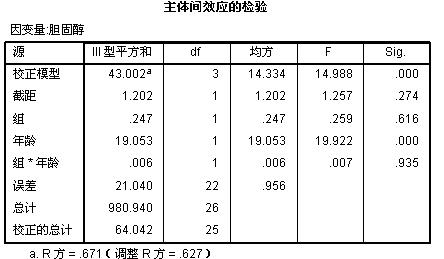
这是主要的统计分析结果,一个典型的方差分析表,解释一下:
1、表格的第一行“校正模型”是对模型的检验,零假设是“模型中所有的因素对因变量均无影响”(这里包括分组、年龄及他们的交互作用),其P<0.001,拒绝零假设,说明存在对因变量有影响的因素。
2、表格的第二行是回归分析的常数项,通常无实际意义。
3、表格的第三行、第四行是对组和年龄的检验,P均<0.05,有统计学意义,说明分组和年龄对胆固醇的影响均有统计学意义。
4、表格的第五行是对分组和年龄的交互作用的检验,其P=0.935>0.05,说明分组和年龄无交互作用,也就是说,年龄对胆固醇的影响不随分组的不同而不同,这也是协方差分析的基本条件之一。这里是满足的。