但对于一台机器而言,将这 10 个对象分类成几个有意义的分组却并不简单——我们知道对于这 10 只虫子,我们可以有 115,975 种不同的分组方式。如果虫子数量增加到 20,那它们可能的分组方法将超过 50 万亿种。要是虫子数量达到 100,那可能的方案数量将超过已知宇宙中的粒子的数量。超过多少呢?据我计算,大约多 500,000,000,000,000,000,000,000,000,000,000,000 倍,已是难以想象的超天文数字!
而我们人类可以做得很快,我们往往会把自己快速分组和理解大量数据的能力看作是理所当然。不管那是一段文本,还是屏幕上图像,或是对象序列,人类通常都能有效地理解自己所面对的数据。
鉴于人工智能和机器学习的关键就是快速理解大量输入数据,那在开发这些技术方面有什么捷径呢?在本文中,你将阅读到两种聚类算法——k-均值聚类和层次聚类,机器可以用其来快速理解大型数据集。
当你事先知道你将找到多少个分组的时候。
工作方式
该算法可以随机将每个观测值(observation)分配到 k 类中的一类,然后计算每个类的平均。接下来,它重新将每个观测值分配到与其最接近的均值的类别,然后再重新计算其均值。这一步不断重复,直到不再需要新的分配为止。
有效案例
假设有一组 9 位足球运动员,他们中每个人都在这一赛季进了一定数量的球(假设在 3-30 之间)。然后我们要将他们分成几组——比如 3 组。
第一步:需要我们将这些运动员随机分成 3 组并计算每一组的均值。
- 第 1 组
- 运动员 A(5 个球)、运动员 B(20 个球)、运动员 C(11 个球)
- 该组平均=(5 + 20 + 11) / 3 = 12
- 第 2 组
- 运动员 D(5 个球)、运动员 E(9 个球)、运动员 F(19 个球)
- 该组平均=11
- 第 3 组
- 运动员 G(30 个球)、运动员 H(3 个球)、运动员 I(15 个球)
- 该组平均=16
- 第 1 组(原来的均值=12)
- 运动员 C(11 个球)、运动员 E(9 个球)
- 新的平均=(11 + 9) / 2 = 10
- 第 2 组(原来的均值=11)
- 运动员 A(5 个球)、运动员 D(5 个球)、运动员 H(3 个球)
- 新的平均=4.33
- 第 3 组(原来的均值=16)
- 运动员 B(20 个球)、运动员 F(19 个球)、运动员 G(30 个球)、运动员 I(15 个球)
- 新的平均=21
- 第 1 组(原来的均值=10)
- 运动员 C(11 个球)、运动员 E(9 个球)、运动员 I(15 个球)
- 最终平均=11.3
- 第 2 组(原来的均值=4.33)
- 运动员 A(5 个球)、运动员 D(5 个球)、运动员 H(3 个球)
- 最终平均=4.33
- 第 3 组(原来的均值=21)
- 运动员 B(20 个球)、运动员 F(19 个球)、运动员 G(30 个球)、
- 最终平均=23
以这种方式,当给定一系列表现统计的数据时,机器就能很好地估计任何足球队的队员的位置——可用于体育分析,也能用于任何将数据集分类为预定义分组的其它目的的分类任务。
上面所描述的算法还有一些变体。最初的「种子」聚类可以通过多种方式完成。这里,我们随机将每位运动员分成了一组,然后计算该组的均值。这会导致最初的均值可能会彼此接近,这会增加后面的步骤。
另一种选择种子聚类的方法是每组仅一位运动员,然后开始将其他运动员分配到与其最接近的组。这样返回的聚类是更敏感的初始种子,从而减少了高度变化的数据集中的重复性。但是,这种方法有可能减少完成该算法所需的迭代次数,因为这些分组实现收敛的时间会变得更少。
K-均值聚类的一个明显限制是你必须事先提供预期聚类数量的假设。目前也存在一些用于评估特定聚类的拟合的方法。比如说,聚类内平方和(Within-Cluster Sum-of-Squares)可以测量每个聚类内的方差。聚类越好,整体 WCSS 就越低。
当我们希望进一步挖掘观测数据的潜在关系,可以使用层次聚类算法。
工作方式
首先我们会计算距离矩阵(distance matrix),其中矩阵的元素(i,j)代表观测值 i 和 j 之间的距离度量。然后将最接近的两个观察值组为一对,并计算它们的平均值。通过将成对观察值合并成一个对象,我们生成一个新的距离矩阵。具体合并的过程即计算每一对最近观察值的均值,并填入新距离矩阵,直到所有观测值都已合并。
有效案例:
以下是关于鲸鱼或海豚物种分类的超简单数据集。作为受过专业教育的生物学家,我可以保证通常我们会使用更加详尽的数据集构建系统。现在我们可以看看这六个物种的典型体长。本案例中我们将使用 2 次重复步骤。
- Species Initials Length(m)
- Bottlenose Dolphin BD 3.0
- Risso's Dolphin RD 3.6
- Pilot Whale PW 6.5
- Killer Whale KW 7.5
- Humpback Whale HW 15.0
- Fin Whale FW 20.0
- BD RD PW KW HW
- RD 0.6
- PW 3.5 2.9
- KW 4.5 3.9 1.0
- HW 12.0 11.4 8.5 7.5
- FW 17.0 16.4 13.5 12.5 5.0
- [BD, RD] PW KW HW
- PW 3.2
- KW 4.2 1.0
- HW 11.7 8.5 7.5
- FW 16.7 13.5 12.5 5.0
随后我们再重复步骤一,再一次计算距离矩阵,只不过现在将领航鲸与逆戟鲸合并成一项且设定长度为 7.0m。
- [BD, RD] [PW, KW] HW
- [PW, KW] 3.7
- HW 11.7 8.0
- FW 16.7 13.0 5.0
- [[BD, RD] , [PW, KW]] HW
- HW 9.8
- FW 14.8 5.0
返回到步骤 1,计算新的距离矩阵,其中座头鲸与长须鲸已经合并为一项。
- [[BD, RD] , [PW, KW]]
- [HW, FW] 12.3
- [[[BD, RD],[PW, KW]],[HW, FW]]
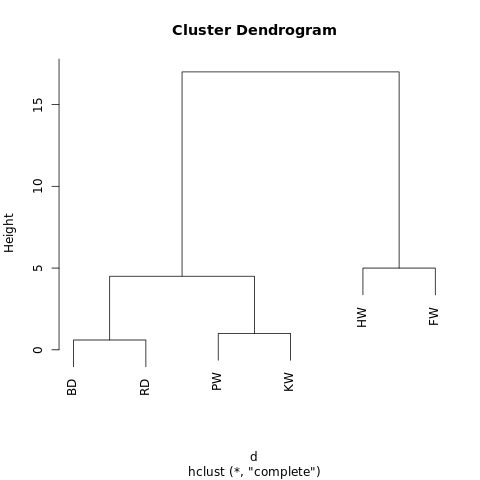
在生物进化学中,通常会使用包含更多物种和测量的大型数据集推断这些物种之间的分类学关系。在生物学之外,层次聚类也在机器学习和数据挖掘中使用。
重要的是,使用这种方法并不需要像 K-均值聚类那样设定分组的数量。你可以通过给定高度「切割」树型以返回分割成的集群。高度的选择可以通过几种方式进行,其取决于我们希望对数据进行聚类的分辨率。
例如上图,如果我们在高度等于 10 的地方画一条线,就将两个主分支切开分为两个子图。如果我们从高度等于 2 的地方分割,就会生成三个聚类。
更多细节:
对于这里给出的层次聚类算法(hierarchical clustering algorithms),其有三个不同的方面。
最根本的方法就是我们所使用的集聚(agglomerative)过程,通过该过程,我们从单个数据点开始迭代,将数据点聚合到一起,直到成为一个大型的聚类。另外一种(更高计算量)的方法从巨型聚类开始,然后将数据分解为更小的聚类,直到独立数据点。
还有一些可以计算距离矩阵的方法,对于很多情况下,欧几里德距离(参考毕达哥拉斯定理)就已经够了,但还有一些可选方案在特殊的情境中更加适用。
最后,连接标准(linkage criterion)也可以改变。聚类根据它们不同的距离而连接,但是我们定义「近距离」的方式是很灵活的。在上面的案例中,我们通过测量每一聚类平均值(即形心(centroid))之间的距离,并与最近的聚类进行配对。但你也许会想用其他定义。
例如,每个聚类有几个离散点组成。我们可以将两个聚类间的距离定义为任意点间的最小(或最大)距离,就如下图所示。还有其他方法定义连接标准,它们可能适应于不同的情景。