SPSS学习笔记之——二项Logistic回归分析

一、 概述

Logistic回归主要用于因变量为分类变量（如疾病的缓解、不缓解，评比中的好、中、差等）的回归分析，自变量可以为分类变量，也可以为连续变量。他可以从多个自变量中选出对因变量有影响的自变量，并可以给出预测公式用于预测。

因变量为二分类的称为二项logistic回归，因变量为多分类的称为多元logistic回归。 

下面学习一下Odds、OR、RR的概念：

在病例对照研究中，可以画出下列的四格表：

------------------------------------------------------

暴露因素              病例             对照

-----------------------------------------------------

暴露                   a                 b 

非暴露               c                 d

-----------------------------------------------

Odds: 称为比值、比数，是指某事件发生的可能性(概率)与不发生的可能性（概率）之比。在病例对照研究中病例组的暴露比值为：

odds1 = (a/(a+c))/(c(a+c)) = a/c，

对照组的暴露比值为：

odds2 = (b/(b+d))/(d/(b+d)) = b/d

OR：比值比，为：病例组的暴露比值(odds1)/对照组的暴露比值(odds2) = ad/bc

换一种角度，暴露组的疾病发生比值：

odds1 = (a/(a+b))/(b(a+b)) = a/b

非暴露组的疾病发生比值：

odds2 = (c/(c+d))/(d/(c+d)) = c/d

OR = odds1/odds2 = ad/bc

与之前的结果一致。

OR的含义与相对危险度相同，指暴露组的疾病危险性为非暴露组的多少倍。OR>1说明疾病的危险度因暴露而增加，暴露与疾病之间为“正”关联；OR<1说明疾病的危险度因暴露而减少，暴露与疾病之间为“负”关联。 还应计算OR的置信区间，若区间跨1，一般说明该因素无意义。

关联强度大致如下：

------------------------------------------------------

      OR值                        联系强度

------------------------------------------------------

0.9-1.0   1.0-1.1                 无

0.7-0.8   1.2-1.4                 弱（前者为负关联，后者为正关联）

0.4-0.6   1.5-2.9                 中等（同上）

0.1-0.3   3.0-9.0                  强（同上）

 <0.1     10.0以上                很强（同上）

------------------------------------------------------

RR: 相对危险度（relative risk）的本质为率比（rate ratio）或危险比(risk ratio)，即暴露组与非暴露组发病率之比，或发病的概率之比。但是病例对照研究不能计算发病率，所以病例对照研究中只能计算OR。当人群中疾病的发病率或者患病率很小时，OR近似等于RR，可用OR值代替RR。

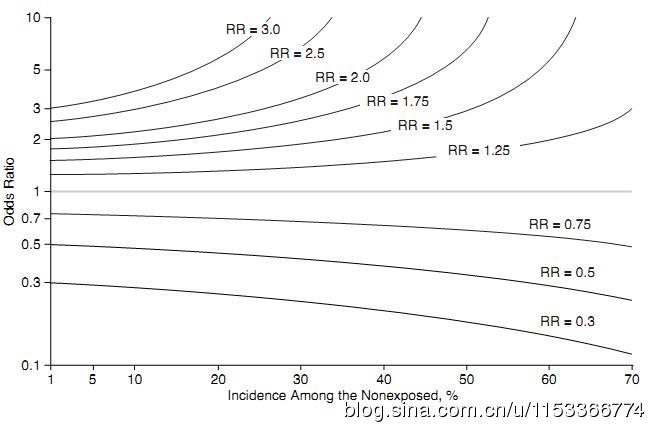
不同发病率情况下，OR与RR的关系图如下：

设疾病在非暴露人群中的发病为P0，则可用下列公式对RR记性校正：

RR = OR/((1-P0)+(P0*OR))

若P0未知，可以用c/(c+d)估计。

二、 问题

对银行拖欠贷款的影响因素进行分析，可选的影响因素有：客户的年龄、教育水平、工龄、居住年限、家庭收入、贷款收入比、信用卡欠款、其他债务等，从中选择出对是否拖欠贷款的预测因素，并进行预测。数据采用SPSS自带的bankloan.sav中的部分数据。

三、 统计操作

1、 准备数据

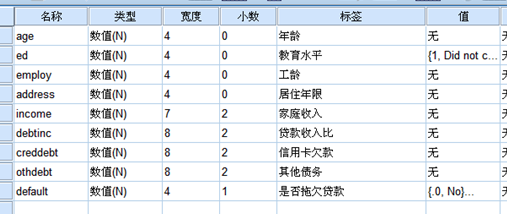
变量视图

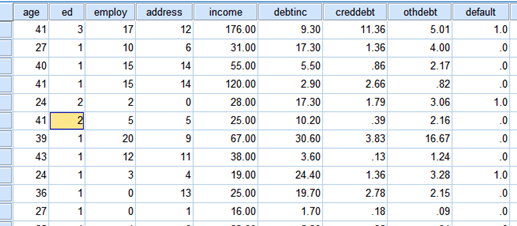
数据视图

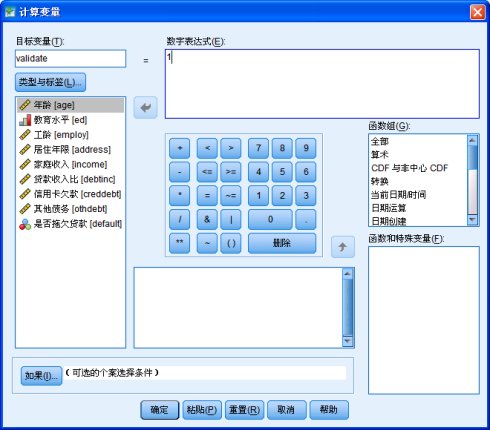
下面开始准备数据：由于“default”变量可能存在缺失值，所以要新建一个变量"validate"，当default不为缺失值时，将validate=1，然后通过validate来判断将不缺失的值纳入回归分析：选择如下菜单：

 

点击进入“计算变量”对话框：

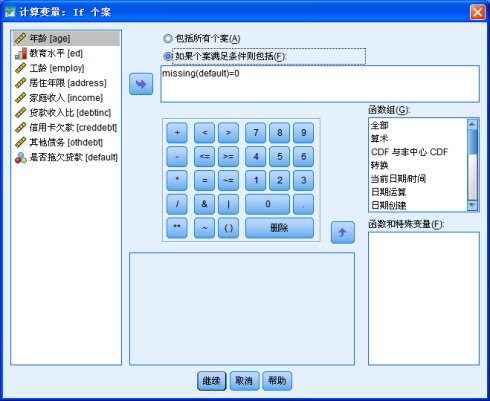
在“目标变量”看中输入“validate”，右边的“数字表达式”输入“1”。再点击下方的“如果...”按钮，进入对话框：

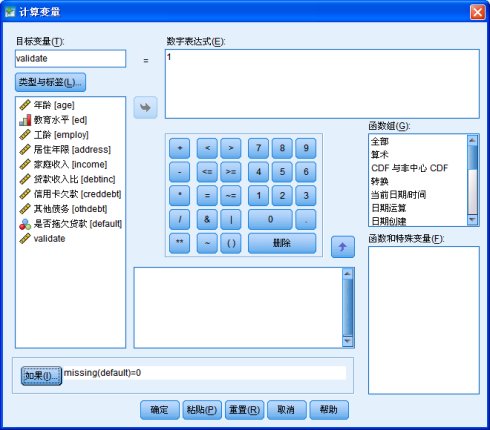
在框中输入missing(default)=0，含义是defalut变量不为缺失值。点击“继续”回到“计算变量”对话框：

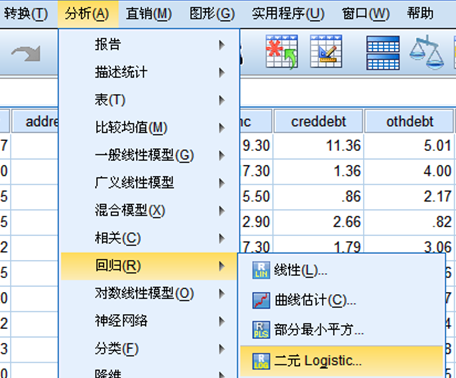
点击确定，完成变量计算。 2、统计菜单选择

进入如下的对话框（下文称“主界面”）：

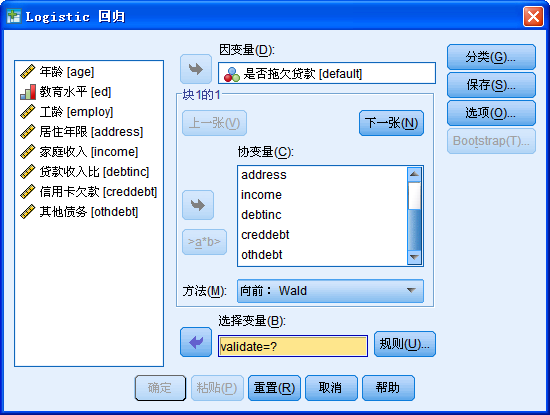
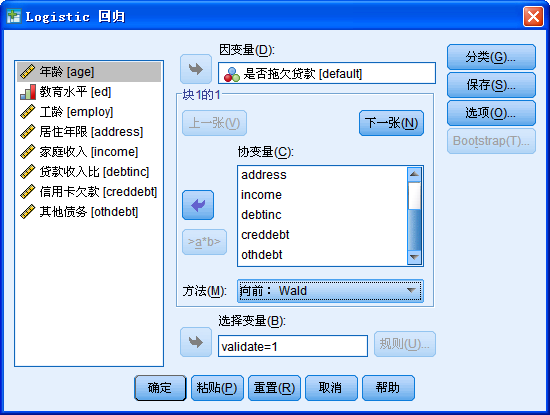
将“是否拖欠贷款[default]”作为因变量选入“因变量”框中。将其与变量选入“协变量”框中，下方的“方法”下拉菜单选择“向前：LR”（即前向的最大似然法，选择变量筛选的方法，条件法和最大似然法较好，慎用Wald法）。将“validate”变量选入下方的“选择变量”框。点击“选择变量”框后的“规则”按钮，进入定义规则对话框：

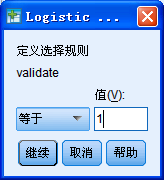
设置条件为“validate=1”，点击“继续”按钮返回主界面：

点击右上角“分类”按钮，进入如下的对话框：

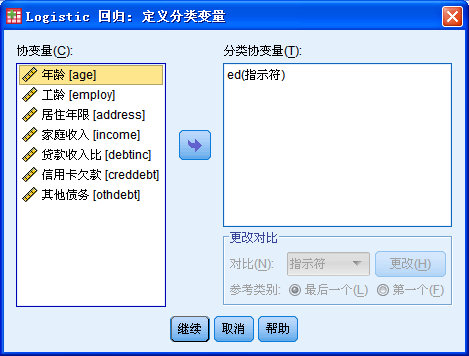
该对话框用来设置自变量中的分类变量，左边的为刚才选入的协变量，必须将所有分类变量选入右边的“分类协变量框中”。本例中只有“教育程度[ed]”为分类变量，将它选入右边框中，下方的“更改对比”可以默认。点击“继续”按钮返回主界面。回到主界面后点击“选项”按钮，进入对话框：

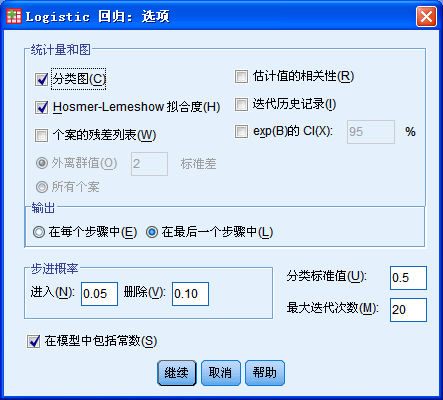
勾选“分类图”和“Hosmer-Lemeshow拟合度”复选框，输出栏中选择“在最后一个步骤中”，其余参数默认即可。“Hosmer-Lemeshow拟合度”能较好的检验该模型的拟合程度。点击继续回到主界面，点击“确定”输出结果。四、结果分析

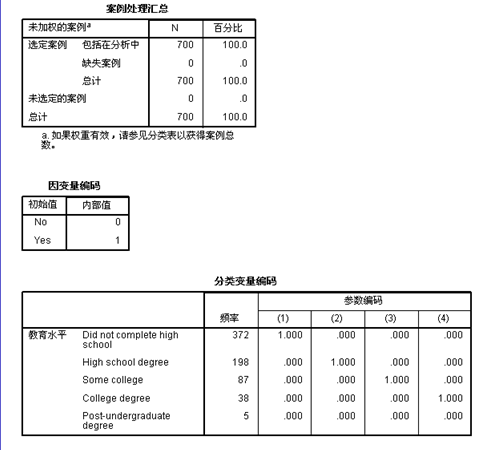
以上是案例处理摘要及变量的编码。

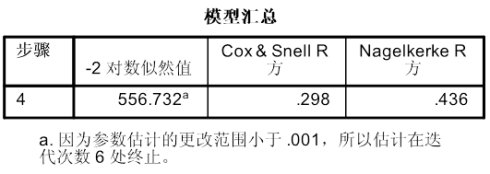
上表是关于模型拟合度的检验。这用Cox&Snell R方和Negelkerke R方代替了线性回归中的R方，他们呢的值越接近1，说明拟合度越好，这个他们分别为0.298和0.436，单纯看这一点，似乎模型的拟合度不好，但是该参数主要是用于模型之间的对比。

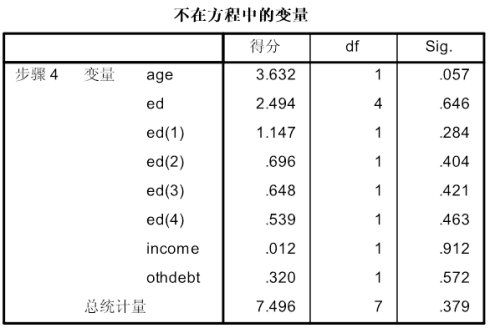
这是H-L检验表，P=0.381 > 0.05接受0假设，认为该模型能很好拟合数据。H-L检验的随机性表，比较观测值与期望值，表中观测值与期望值大致相同，可以直观的认为，该模型拟合度较好。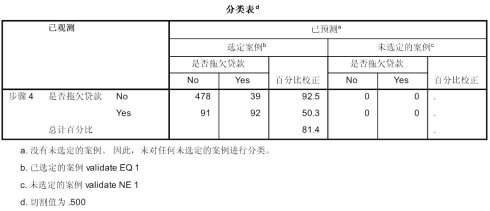

这个是最终模型的预测结果列联表。在700例数据中进行预测，在未拖欠贷款的478+39=517例中，有478例预测正确，正确率92.5%；在91+92=183例拖欠贷款的用户中，有92例预测正确，正确率50.3%。总的正确率81.4%。可以看出该模型对于非拖欠贷款者预测效果较好。

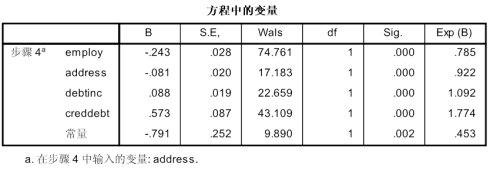
这是最终拟合的结果，四个变量入选，P值均<0.05。列“B”为偏回归系数，“S.E.”为标准误差，“Wals”为Wald统计量。“EXP(B)”即为相应变量的OR值（又叫优势比，比值比），为在其他条件不变的情况下，自变量每改变1个单位，事件的发生比“Odds”的变化率。如工龄为2年的用户的拖欠贷款的发生比（Odds）是工龄为1年的用户的0.785倍。最终的拟合方程式：logit(P)  =  -0.791 - 0.243*employ - 0.081*address + 0.088*detbinc + 0.573*creddebt。用该方程可以做预测，预测值大于0.5说明用户可能会拖欠贷款，小于0.5说明可能不会拖欠贷款。

这是不在方程中的变量，其P均大于0.05，没有统计学意义。

这是预测概率的直方图。横轴为拖欠贷款的预测概率（0为不拖欠，1为拖欠），纵轴为观测的频数，符号“Y”代表拖欠，“N”代表不拖欠。若预测正确，所有的Y均应在横轴0.5分界点的右边，所有的N均应该在0.5分界点的左边，数据分布为“U”型，中间数据少，两头数据多。可以直观的看出，本模型对于不拖欠贷款的预测较好，对于拖欠贷款的预测相对较差。