序列的相似性

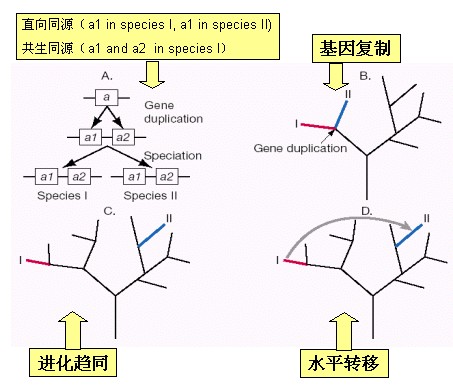
序列的相似性可以是定量的数值，也可以是定性的描述。相似度是一个数值，反映两条序列的相似程度。关于两条序列之间的关系，有许多名词，如相同、相似、同源、同功、直向同源、共生同源等。在进行序列比较时经常使用“同源”（homology）和“相似”（similarity）这两个概念，这是两个经常容易被混淆的不同概念。两条序列同源是指它们具有共同的祖先。在这个意义上，无所谓同源的程度，两条序列要么同源，要么不同源。而相似则是有程度的差别，如两条序列的相似程度达到30%或60%。一般来说，相似性很高的两条序列往往具有同源关系。但也有例外，即两条序列的相似性很高，但它们可能并不是同源序列，这两条序列的相似性可能是由随机因素所产生的，这在进化上称为“趋同”（convergence），这样一对序列可称为同功序列。直向同源（orthologous）序列是来自于不同的种属同源序列，而共生同源（paralogous）序列则是来自于同一种属的序列，它是由进化过程中的序列复制而产生的。

序列比较的基本操作是比对（align）。两条序列的比对（alignment）是指这两条序列中各个字符的一种一一对应关系，或字符对比排列。序列的比对是一种关于序列相似性的定性描述，它反映在什么部位两条序列相似，在什么部位两条序列存在差别。最优比对揭示两条序列的最大相似程度，指出序列之间的根本差异。

字母表和序列

在生物分子信息处理过程中，将生物分子序列抽象为字符串，其中的字符取自特定的字母表。字母表是一组符号或字符，字母表中的元素组成序列。一些重要的字母表有：

（1）4字符DNA字母表 {A, C, G, T}；

（2）扩展的遗传学字母表或IUPAC编码；

（3）单字母氨基酸编码；

（4）上述字母表形成的子集。

下面所讨论的内容独立于特定的字母表。 首先规定一些特定的符号：

① A — 字母表；

② A* — 由字母表A中字符所形成的一系列有限长度序列或字符串的集合；

③ a、b、c — 单独的字符；

④ s、t、u、v、x — A*中的序列；

⑤ |s| — 序列s的长度。

为了说明序列s的子序列和s中单个字符，我们在s中各字符之间用数字标明分割边界。例如，设s=ACCACGTA，则s可表示为

0A1C2C3A4C5G6T7A8 。

i:s:j 指明第i位或第j位之间的子序列。当然，0 £ i £ j £ |s|。子序列0 : s : i 称为前缀，即prefix(s,i)，而子序列 i:s:|s| 称为后缀suffix(s, |s|-i+1)。有两种特殊的情况，即 i=j或i = j-1。

① i:s:i 表示空序列

② ( j-1):s: j 表示s 中的第j 个字符，简记为sj 。

一般认为，子序列与计算机算法中子串的概念相当。但是，严格地讲，子序列与子串的概念是有区别的：子串是子序列，而子序列不一定是子串。可以通过选取s中的某些字符（或删除s中的某些字符）而形成s的子序列，例如TTT是ATATAT的子序列。而s的子串则是由s中相继的字符所组成，例如TAC是AGTACA的子串，但不是TTGAC的子串。如果t是s的子串，则称s是t的超串。子串也可以称为连续子序列。

两条序列s和t的连接用s + + t来表示，如：

ACC++CTA = ACCCTA

字符串操作除连接操作之外，另有一个k操作，即删除一个字符串两端的字符。其定义如下：

prefix(s,l) = sk|s|-l ，

suffix(s,l) = k|s|-ls ，

i:s:j = ki-1sk|s|-j 。

序列比较可以分为四种基本情况，具体任务和应用说明如下：

（1）假设有两条长度相近的、来自同一个字母表的序列，它们之间非常相似，仅仅是有一些细微的差别，例如字符的插入、字符的删除和字符替换，要求找出这两条序列的差别。这种操作实际应用比较多，例如，有两个实验室同时测定某个基因的DNA序列，其结果可能不一样，需要通过序列比较来比较实验结果。

（2）假设有两条序列，要求判断是否有一条序列的前缀与另一条序列的后缀相似，如果是，则分别取出前缀和后缀。该操作常用于大规模DNA测序中序列片段的组装。

（3）假设有两条序列，要求判断其中的一条序列是否是另一条序列的子序列。这种操作常用于搜索特定的序列模式。

（4）假设有两条序列，要求判断这两条序列中是否有非常相似的子序列。这种操作可用于分析保守序列。

当然，进行序列比较时，往往还需要说明是采取全局比较，还是采取局部比较。全局比较是比较两条完整的序列，而局部比较是找出最大相似的子序列。

编辑距离（Edit Distance）

观察这样两条DNA序列：GCATGACGAATCAG和TATGACAAACAGC。一眼看上去，这两条序列并没有什么相似之处，然而如果将第二条序列错移一位，并对比排列起来以后，就可以发现它们的相似性。

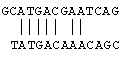
如果进一步在第二条序列中加上一条短横线，就会发现原来这两条序列有更多的相似之处。

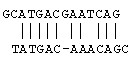
上面是两条序列相似性的一种定性表示方法，为了说明两条序列的相似程度，还需要定量计算。有两种方法可用于量化两条序列的相似程度：一为相似度，它是两条序列的函数，其值越大，表示两条序列越相似；与相似度对应的另一个概念是两条序列之间的距离，距离越大，则两条序列的相似度就越小。在大多数情况下，相似度和距离可以交互使用，并且距离越大，相似度越小，反之亦然。但一般而言，相似度使用得较多，并且灵活多变。

最简单的距离就是海明（Hamming）距离。对于两条长度相等的序列，海明距离等于对应位置字符不同的个数。例如，下图是3组序列海明距离的计算结果。

使用距离来计算不够灵活，这是因为序列可能具有不同的长度，两条序列中各位置上的字符并不一定是真正的对应关系。例如，在DNA复制的过程中，可能会发生像删除或插入一个碱基这样的错误，虽然两条序列的其他部分相同，但由于位置的移动导致海明距离的失真。就图3.1中例子最右边的情况，海明距离为6，简单地从海明距离来看，两条序列差别很大（整个序列的长度只有8bp），但是，如果从s中删除G，从t中删除T，则两条序列都成为ACACACA，这说明两条序列仅仅相差两个字符。实际上，在许多情况下，直接运用海明距离来衡量两条序列的相似程度是不合理的。

为了解决字符插入和删除问题，引入字符“编辑操作”（Edit Operation）的概念，通过编辑操作将一个序列转化为一个新序列。用一个新的字符“-”代表空位（或空缺，Space），并定义下述字符编辑操作：

Match（a，a） — 字符匹配；

Delete（a，-） — 从第一条序列删除一个字符，或在第二条序列相应的位置插入空白字符；

Replace（a，b） — 以第二条序列中的字符b替换第一条序列中的字符a，a¹b；

Insert（-，b） — 在第一条序列插入空位字符，或删除第二条序列中的对应字符b。

很显然，在比较两条序列s和t时，在s中的一个删除操作等价于在t中对应位置上的一个插入操作，反之亦然。需要注意的是，两个空位字符不能匹配，因为这样的操作没有意义。引入上述编辑操作后，重新计算两条序列的距离，就成为编辑距离。

以上的操作仅仅是关于序列的常用操作，在实际应用中还可以引入复杂的序列操作。下面是两条序列的一种比对：

上述比对不能反映两条序列的本质关系。但是，如果将第二条序列头尾倒置，可以发现两条序列惊人的相似：

再比如，下面两条序列有什么关系？如果将其中一条序列中的碱基替换为其互补碱基，就会发现其中的关系：

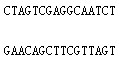
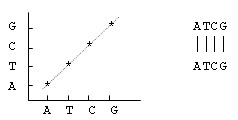
通过点矩阵分析两条序列的相似之处

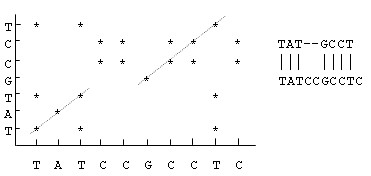
进行序列比较的一个简单的方法是“矩阵作图法”或“对角线作图”，这种方法是由Gibb首先提出的。将两条待比较的序列分别放在矩阵的两个轴上，一条在X轴上，从左到右，一条在Y轴上，从下往上，如图3.2所示。当对应的行与列的序列字符匹配时，则在矩阵对应的位置作出“点”标记。逐个比较所有的字符对，最终形成点矩阵。

序列比较矩阵标记图

显然，如果两条序列完全相同，则在点矩阵主对角线的位置都有标记；如果两条序列存在相同的子串，则对于每一个相同的子串对，有一条与对角线平行的由标记点所组成的斜线，如图a中的斜线代表相同的子串“ATCC”；而对于两条互为反向的序列，则在反对角线方向上有标记点组成的斜线，如图b所示。

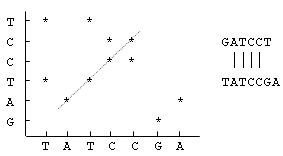
a:相同子串矩阵标记图

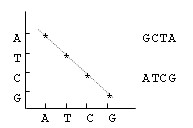
b:反向序列矩阵标记图

对于矩阵标记图中非重叠的与对角线平行斜线，可以组合起来，形成两条序列的一种比对。在两条子序列的中间可以插入符号“-”，表示插入空位字符。在这种对比之下分析两条序列的相似性，如下图所示。找两条序列的最佳比对（对应位置等同字符最多），实际上就是在矩阵标记图中找非重叠平行斜线最长的组合。

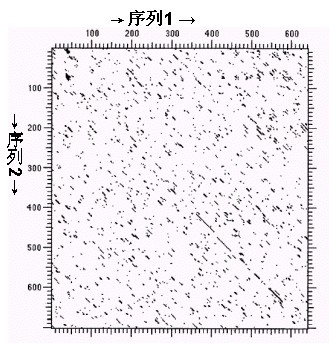
除非已经知道待比较的序列非常相似，一般先用点矩阵方法比较，因为这种方法可以通过观察矩阵的对角线迅速发现可能的序列比对。

实例一：

实例二：

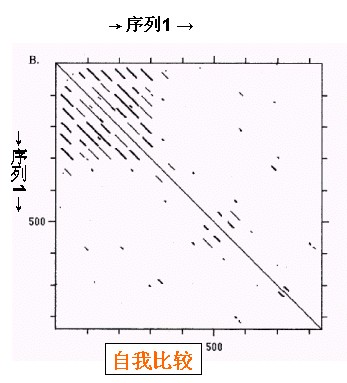
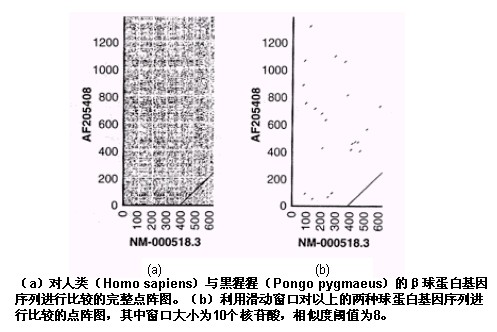
两条序列中有很多匹配的字符对，因而在点矩阵中会形成很多点标记。当对比较长的序列进行比较时，这样的点阵图很快会变得非常复杂和模糊。使用滑动窗口代替一次一个位点的比较是解决这个问题的有效方法。假设窗口大小为10，相似度阈值为8。首先，将X轴序列的第1-10个字符与Y轴序列的第1-10个字符进行比较。如果在第一次比较中，这10个字符中有8个或者8个以上相同，那么就在点阵空间（1,1）的位置画上点标记。然后窗口沿X轴向右移动一个字符的位置，比较X轴序列的第2-11个字符与Y轴序列的第1-10个字符。不断重复这个过程，直到X轴上所有长度为10的子串都与Y轴第1-10个字符组成的子串比较过为止。然后，将Y轴的窗口向上移动一个字符的位置，重复以上过程，直到两条序列中所有长度为10的子串都被两两比较过为止。基于滑动窗口的点矩阵方法可以明显地降低点阵图的噪声，并且可以明确地指出两条序列间具有显著相似性的区域。

序列的两两比对

序列的两两比对（Pairwise Sequence Alignment）就是对两条序列进行编辑操作，通过字符匹配和替换，或者插入和删除字符，使得两条序列达到一样的长度，并使两条序列中相同的字符尽可能地一一对应。设两条序列分别是s和t，在s或t中插入空位符号，使s和t达到一样的长度。下图是对序列AGCACACA和ACACACTA的两种比对结果以及对应的字符编辑操作。

下面就不同类型的编辑操作定义函数w，它表示“代价（cost）”或“权重（weight）”。对字母表A中的任意字符a、b，定义：

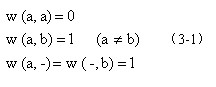
这是一种简单的代价定义，在实际应用中还需使用更复杂的代价模型。一方面，可以改变各编辑操作的代价值，例如，在蛋白质序列比较时，用理化性质相近的氨基酸进行替换的代价应该比完全不同的氨基酸替换代价小；另一方面，也可以使用得分（score）函数来评价编辑操作。下面给出一种基本的得分函数：

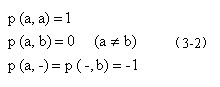
在进行序列比对时，可根据实际情况选用代价函数或得分函数，即选用（3-1）式或（3-2）式。

下面给出在进行序列比对时常用的概念：

（1）两条序列s 和 t 的比对的得分（或代价）等于将s 转化为t 所用的所有编辑操作的得分（或代价）总和；

（2）s 和t 的最优比对是所有可能的比对中得分最高（或代价最小）的一个比对；

（3）s 和t 的真实距离应该是在得分函数p值（或代价函数w值）最优时的距离。

使用前面代价函数w的定义，可以得到下列比对的代价：

s: AGCACAC-A

t: A-CACACTA

cost（s，t）= 2

而使用得分函数p 的定义，可以得到下列比对的得分：

s: AGCACAC-A

t: A-CACACTA

score (s，t)= 5

进行序列比对的目的是寻找一个得分最高（或代价最小）的比对。

用于序列相似性的打分矩阵（scoring matrix）

无论是3-1式还是3-2式，都是简单相似性评价模型，在计算比对的代价或得分时，对字符替换操作只进行统一的处理，没有考虑“同类字符”替换与“非同类字符”替换的差别。实际上，不同类型的字符替换，其代价或得分是不一样的，特别是对于蛋白质序列。某些氨基酸可以很容易地相互取代而不用改变它们的理化性质。例如，考虑这样两条蛋白质序列，其中一条在某一位置上是丙氨酸，如果该位点被替换成另一个较小且疏水的氨基酸，比如缬氨酸，那么对蛋白质功能的影响可能较小；如果被替换成较大且带电的残基，比如赖氨酸，那么对蛋白功能的影响可能就要比前者大。直观地讲，比较保守的替换比起较随机替换更可能维持蛋白质的功能，且更不容易被淘汰。因此，在为比对打分时，我们可能更倾向对丙氨酸与缬氨酸的比对位点多些奖励，而对于丙氨酸与那些大而带电氨基酸（比如赖氨酸）的比对位点则相反。理化性质相近的氨基酸残基之间替换的代价显然应该比理化性质相差甚远的氨基酸残基替换得分高，或者代价小。同样，保守的氨基酸替换得分应该高于非保守的氨基酸替换。这样的打分方法在比对非常相近的序列以及差异极大的序列时，会得出不同的分值。这就是提出打分矩阵（或者称为取代矩阵）的原由。在打分矩阵中，详细地列出各种字符替换的得分，从而使得计算序列之间的相似度更为合理。在比较蛋白质时，我们可以用打分矩阵来增强序列比对的敏感性。打分矩阵是序列比较的基础，选择不同的打分矩阵将得到不同的比较结果，而了解打分矩阵的理论依据将有助于在实际应用中选择合适的打分矩阵。以下介绍一些常用的打分矩阵或代价矩阵。

1、核酸打分矩阵

设核酸序列所用的字母表为 A = { A，C，G，T }。

（1）等价矩阵

等价矩阵（见表3.1）是最简单的一种打分矩阵，其中，相同核苷酸匹配的得分为“1”，而不同核苷酸的替换得分为“0”（没有得分）。

（2）BLAST矩阵

BLAST是目前最流行的核酸序列比较程序，表3.2是其打分矩阵。这也是一个非常简单的矩阵，如果被比的两个核苷酸相同，则得分为“+5”，反之得分为“-4”。

（3）转换-颠换矩阵

核酸的碱基按照环结构分为两类，一类是嘌呤（腺嘌呤A，鸟嘌呤G），它们有两个环；另一类是嘧啶（胞嘧啶C，胸腺嘧啶T），它们的碱基只有一个环。如果DNA碱基的变化（碱基替换）保持环数不变，则称为转换（transition），如A->G，C->T；如果环数发生变化，则称为颠换（transversion），如A®C，A®T等。在进化过程中，转换发生的频率远比颠换高，而表3.3所示的矩阵正好反映了这种情况，其中转换的得分为“-1”，而颠换的得分为“-5”。

2、蛋白质打分矩阵

（1）等价矩阵

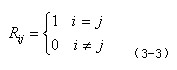
其中，Rij代表打分矩阵元素，i、j分别代表字母表第i个和第j个字符。

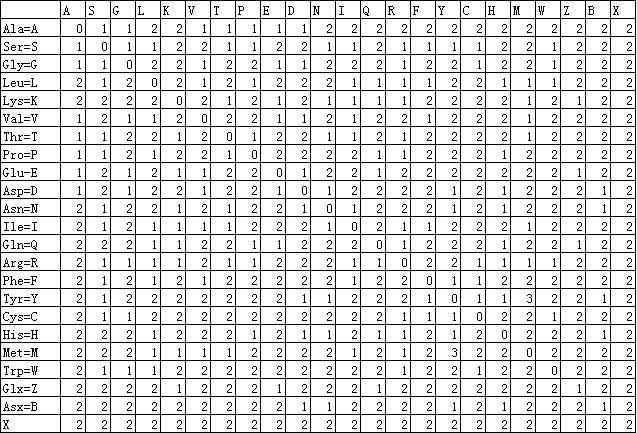
（2）遗传密码矩阵GCM

GCM矩阵通过计算一个氨基酸残基转变到另一个氨基酸残基所需的密码子变化数目而得到，矩阵元素的值对应于代价。如果变化一个碱基，就可以使一个氨基酸的密码子改变为另一个氨基酸的密码子，则这两个氨基酸的替换代价为1；如果需要2个碱基的改变，则替换代价为2；以此类推（见表3.4）。注意，Met到Tyr的转变是仅有的密码子三个位置都发生变化的转换。在表3.4中，Glx代表Gly、Gln或Glu，而Asx则代表Asn或Asp，X代表任意氨基酸。GCM常用于进化距离的计算，其优点是计算结果可以直接用于绘制进化树，但是它在蛋白质序列比对尤其是相似程度很低的序列比对中很少被使用。

（3）疏水矩阵

该矩阵（见表3.5）是根据氨基酸残基替换前后疏水性的变化而得到得分矩阵。若一次氨基酸替换疏水特性不发生太大的变化，则这种替换得分高，否则替换得分低。

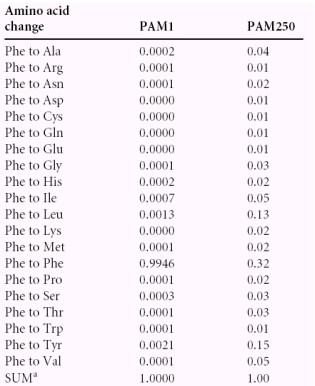
（4）PAM矩阵

为了得到打分矩阵，更常用的方法是统计自然界中各种氨基酸残基的相互替换率。如果两种特定的氨基酸之间替换发生得比较频繁，那么这一对氨基酸在打分矩阵中的互换得分就比较高。PAM矩阵就是这样一种打分矩阵。PAM矩阵是第一个广泛使用的最优矩阵，它是基于进化原理的，建立在进化的点接受突变模型PAM（Point Accepted Mutation）基础上，通过统计相似序列比对中的各种氨基酸替换发生率而得到该矩阵。Dayhoff和她的同事们研究了71个相关蛋白质家族的1572个突变，发现蛋白质家族中氨基酸的替换并不是随机的，由此，断言一些氨基酸的替换比其他替换更容易发生，其主要原因是这些替换不会对蛋白质的结构和功能产生太大的影响。如果氨基酸的替换是随机的，那么，每一种可能的取代频率仅仅取决于不同氨基酸出现的背景频率。然而，在相关蛋白中，存在取代频率大大地倾向于那些不影响蛋白质功能的取代，换句话说，这些点突变已经被进化所接受。这意味着，在进化历程上，相关的蛋白质在某些位置上可以出现不同的氨基酸。

一个PAM就是一个进化的变异单位，即1%的氨基酸改变。但是，这并不意味着经过100次PAM后，每个氨基酸都发生变化，因为其中一些位置可能会经过多次改变，甚至可能变回到原先的氨基酸。因此，另外一些氨基酸可能不发生改变。PAM有一系列的替换矩阵，每个矩阵用于比较具有特定进化距离的两条序列。例如，PAM-120矩阵用于比较相距120个PAM单位的序列。一个PAM-N矩阵元素（i，j）的值反映两条相距N个PAM单位的序列中第i种氨基酸替换第j种氨基酸的概率。从理论上讲，PAM-0是一个单位矩阵，主对角线上的元素值为1，其它矩阵元素的值为0。其他PAM-N矩阵可以通过统计计算而得到。首先针对那些确信是相距一个PAM单位的序列进行统计分析，得到PAM-1矩阵。PAM-1矩阵对角线上的元素值接近于1，而其它矩阵元素值接近于0。例如，可以按下述方法构建PAM-1矩阵。首先，构建一个序列间相似度很高（通常大于85％）的比对。接着，计算每个氨基酸j的相对突变率mj。相对突变率就是某种氨基酸被其它任意氨基酸替换的次数。比如，丙氨酸的相对突变率是通过计算丙氨酸与非丙氨酸残基比对的次数来得到。然后，针对每个氨基酸对i和j，计算氨基酸j被氨基酸i替换的次数。最后，将以上替换次数除以对应的相对替换率，利用每个氨基酸出现的频度对其进行标准化，并将以上计算结果取常用对数，于是得到了PAM-1矩阵中的元素PAM-1（i，j）。这种矩阵被称作对数几率矩阵(log odds matrix)，因为其中的元素是根据每个氨基酸替换率的对数值来得到的。

将PAM-1自乘N次，可以得到矩阵PAM-N。虽然Dayhoff等人只发表了PAM-250，但潜在的突变数据可以外推至其他PAM值，产生一组矩阵。可以根据待比较序列的长度以及序列间的先验相似程度来选用特定的PAM矩阵，以发现最适合的序列比对。一般，在比较差异极大的序列时，通常在较高的PAM值处得到最佳结果，比如在PAM-200到PAM-250之间，而较低值的PAM矩阵一般用于高度相似的序列。实践中用得最多的且比较折衷的矩阵是PAM-250。

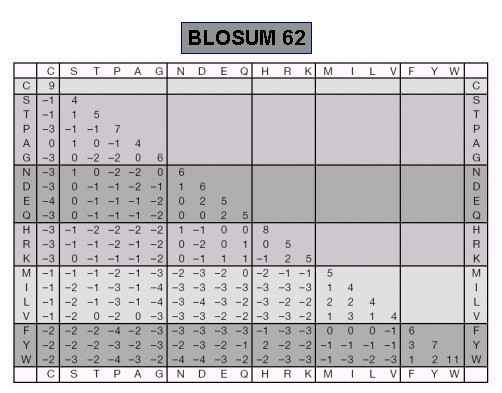
（5）BLOSUM矩阵

BLOSUM矩阵是由Henikoff首先提出的另一种氨基酸替换矩阵，它也是通过统计相似蛋白质序列的替换率而得到的。PAM矩阵是从蛋白质序列的全局比对结果推导出来的，而BLOSUM矩阵则是从蛋白质序列块（短序列）比对而推导出来的。但在评估氨基酸替换频率时，应用了不同的策略。基本数据来源于BLOCKS数据库，其中包括了局部多重比对（包含较远的相关序列，与在PAM中使用较近的相关序列相反）。虽然在这种情况下没有用进化模型，但它的优点在于可以通过直接观察而不是通过外推获得数据。同PAM模型一样，也有一系列的BLOSUM矩阵，可以根据亲缘关系的不同来选择不同的BLOSUM矩阵进行序列比较。然而，BLOSUM矩阵阶数的意义与PAM矩阵正好相反。低阶PAM矩阵适合用来比较亲缘较近的序列，而低阶BLOSUM矩阵更多是用来比较亲缘较远的序列。一般来说，BLOSUM-62矩阵适于用来比较大约具有62％相似度的序列，而BLOSUM-80矩阵更适合于相似度为80%左右的序列。