相似度计算之曼哈顿距离

曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

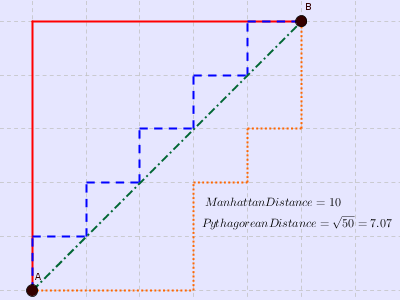
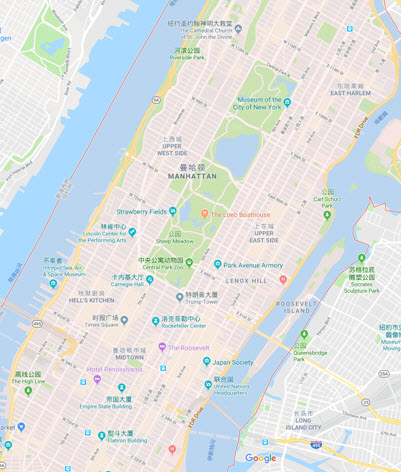
上图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和橙色代表等价的曼哈顿距离。通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”，此即曼哈顿距离名称的来源，同时，曼哈顿距离也称为城市街区距离(City Block distance)。正正方方的曼哈顿的地图：

曼哈顿距离公式：  

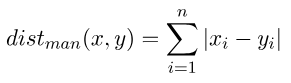
曼哈顿距离的Python实现：

import numpy as np
def manhattan_distance(p_vec, q_vec):
    """
    This method implements the manhattan distance metric
    :param p_vec: vector one
    :param q_vec: vector two
    :return: the manhattan distance between vector one and two
    """
    return np.sum(np.fabs(p_vec - q_vec))