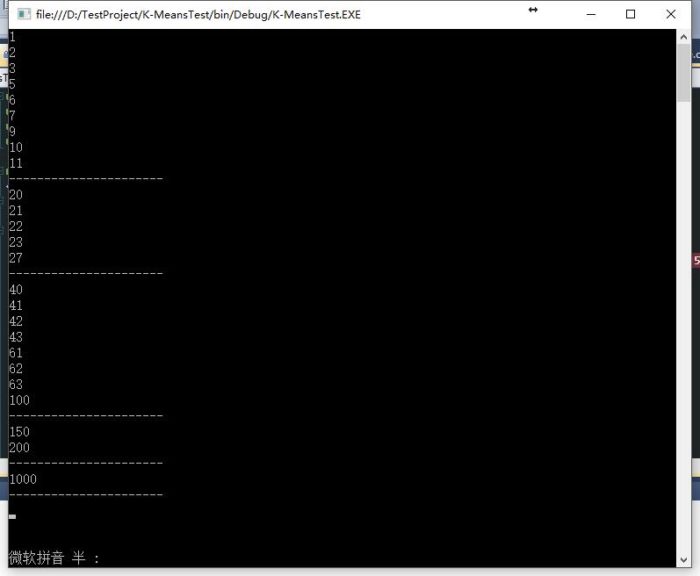
刚看了这个算法,理解如下,放在这里,备忘,如有错误的地方,请指出,谢谢
需要做聚类的数组我们称之为【源数组】
需要一个分组个数K变量来标记需要分多少个组,这个数组我们称之为【聚类中心数组】及
一个缓存临时聚类中心的数组,我们称之为【缓存聚类中心数组】
然后初始化一个K长度的数组,值随机(尽量分布在原数组的更大的区间以便计算),用于和源数组进行比对计算。
下面是计算的部分:
死循环遍历对源数据进行分组。
分组内遍历原数组的每个元素与聚类中心的每个元素的距离(差值的绝对值),将最小距离的聚类中心数组下标缓存的临时变量临时变量数组A中(长度=原数组),
创建二维数组,我们称之为【分组数组】 [聚类中心数组长度][源数组中分类的值],
遍历临时变量数组A,使用A的小标拿到原数组对应的值,赋值给分组数组。
具体公式如:
分组数组[A[i]].add(原数组[i]);
返回分组数组
对分组后的数组计算中间值存入缓存聚类中心数组,比较缓存剧烈数组和聚类数组,是否位置一样,值一样,如果一样跳出死循环,分类结束,
否则将临时剧烈中心数组赋值给聚类中心数组进行下次循环
- using System;
- using System.Collections.Generic;
- using System.Linq;
- using System.Text;
- namespace K_MeansTest
- {
- class Program
- {
- static void Main(string[] args)
- {
- double[] p = { 1, 2, 3, 5, 6, 7, 9, 10, 11,20,21,22,23,27,40,41,42,43,61,62,63, 100, 150, 200, 1000 };
- int k = 5;
- double[][] g;
- g = cluster(p, k);
- for (int i = 0; i < g.Length; i++)
- {
- for (int j = 0; j < g[i].Length; j++)
- {
- Console.WriteLine(g[i][j]);
- }
- Console.WriteLine("----------------------");
- }
- Console.ReadKey();
- }
- /*
- * 聚类函数主体。
- * 针对一维 double 数组。指定聚类数目 k。
- * 将数据聚成 k 类。
- */
- public static double[][] cluster(double[] p, int k)
- {
- // 存放聚类旧的聚类中心
- double[] c = new double[k];
- // 存放新计算的聚类中心
- double[] nc = new double[k];
- // 存放放回结果
- double[][] g;
- // 初始化聚类中心
- // 经典方法是随机选取 k 个
- // 本例中采用前 k 个作为聚类中心
- // 聚类中心的选取不影响最终结果
- for (int i = 0; i < k; i++)
- c[i] = p[i];
- // 循环聚类,更新聚类中心
- // 到聚类中心不变为止
- while (true)
- {
- // 根据聚类中心将元素分类
- g = group(p, c);
- // 计算分类后的聚类中心
- for (int i = 0; i < g.Length; i++)
- {
- nc[i] = center(g[i]);
- }
- // 如果聚类中心不同
- if (!equal(nc, c))
- {
- // 为下一次聚类准备
- c = nc;
- nc = new double[k];
- }
- else // 聚类结束
- break;
- }
- // 返回聚类结果
- return g;
- }
- /*
- * 聚类中心函数
- * 简单的一维聚类返回其算数平均值
- * 可扩展
- */
- public static double center(double[] p)
- {
- return sum(p) / p.Length;
- }
- /*
- * 给定 double 型数组 p 和聚类中心 c。
- * 根据 c 将 p 中元素聚类。返回二维数组。
- * 存放各组元素。
- */
- public static double[][] group(double[] p, double[] c)
- {
- // 中间变量,用来分组标记
- int[] gi = new int[p.Length];
- // 考察每一个元素 pi 同聚类中心 cj 的距离
- // pi 与 cj 的距离最小则归为 j 类
- for (int i = 0; i < p.Length; i++)
- {
- // 存放距离
- double[] d = new double[c.Length];
- // 计算到每个聚类中心的距离
- for (int j = 0; j < c.Length; j++)
- {
- d[j] = distance(p[i], c[j]);
- }
- // 找出最小距离
- int ci = min(d);
- // 标记属于哪一组
- gi[i] = ci;
- }
- // 存放分组结果
- double[][] g = new double[c.Length][];
- // 遍历每个聚类中心,分组
- for (int i = 0; i < c.Length; i++)
- {
- // 中间变量,记录聚类后每一组的大小
- int s = 0;
- // 计算每一组的长度
- for (int j = 0; j < gi.Length; j++)
- if (gi[j] == i)
- s++;
- // 存储每一组的成员
- g[i] = new double
展开收缩;- s = 0;
- // 根据分组标记将各元素归位
- for (int j = 0; j < gi.Length; j++)
- if (gi[j] == i)
- {
- g[i]
展开收缩= p[j];- s++;
- }
- }
- // 返回分组结果
- return g;
- }
- /*
- * 计算两个点之间的距离, 这里采用最简单得一维欧氏距离, 可扩展。
- */
- public static double distance(double x, double y)
- {
- return Math.Abs(x - y);
- }
- /*
- * 返回给定 double 数组各元素之和。
- */
- public static double sum(double[] p)
- {
- double sum = 0.0;
- for (int i = 0; i < p.Length; i++)
- sum += p[i];
- return sum;
- }
- /*
- * 给定 double 类型数组,返回最小值得下标。
- */
- public static int min(double[] p)
- {
- int i = 0;
- double m = p[0];
- for (int j = 1; j < p.Length; j++)
- {
- if (p[j] < m)
- {
- i = j;
- m = p[j];
- }
- }
- return i;
- }
- /*
- * 判断两个 double 数组是否相等。 长度一样且对应位置值相同返回真。
- */
- public static bool equal(double[] a, double[] b)
- {
- if (a.Length != b.Length)
- return false;
- else
- {
- for (int i = 0; i < a.Length; i++)
- {
- if (a[i] != b[i])
- return false;
- }
- }
- return true;
- }
- }
- }