几年前,我写过一个关于t-SNE原理的介绍博客,在日常的工作中,涉及到数据可视化的时候一般都会想到去使用这个工具。但是使用归使用,大部分人却很少去思考为什么要用t-SNE,怎样“正确”的使用t-SNE。有的同学可能会觉得奇怪,就一个可视化分析的方法而已,怎么还涉及到了用法的“正确”与“错误”了呢?事实上,正是因为很多人对t-SNE的细节不甚了解,将其他传统的可视化方法的认知套用在了t-SNE上,犯了错误还浑然不知,进而得出了一些看似正确合理的结论。
在刚刚结束的CVPR 2018上,t-SNE的原作者Laurens亲自出来做了一个tutorial,标题是Do's and Don'ts of using t-SNE to Understand Vision Models,里面列举了很多错误的使用t-SNE的范例,这里作一个简短的笔记分享,重温一下这个经典的方法,同时也加深对一些细节问题的理解。
0x01 基本原理
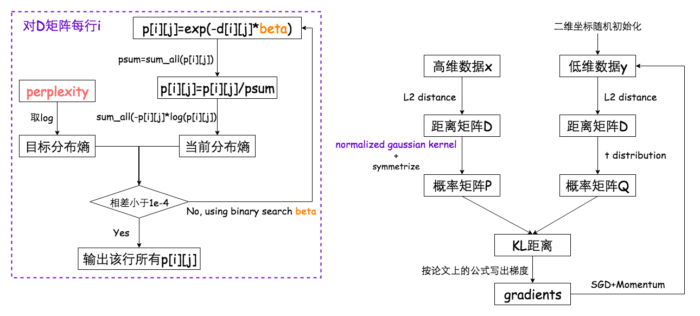
t-SNE本质上是基于流行学习(manifold learning)的降维算法,不同于传统的PCA和MMD等方法,t-SNE在高维用normalized Gaussian kernel对数据点对进行相似性建模。相应的,在低维用t分布对数据点对进行相似性(直观上的距离)建模,然后用KL距离来拉近高维和低维空间中的距离分布。这一块就不具体展开了。
如果想对t-SNE的算法原理有更深入的认识,还是建议大家认真阅读一版t-SNE的实现的代码,很多模糊不清的地方看了代码之后自然就很明了,我推荐这个Javascript版本的代码,逻辑结构非常清晰,我在此基础上增加了一些简略的注释,放到了我的gist上了(需要梯子),这里再列出一个算法流程图,辅助理解。
0x02 错误案例
下面我们就具体了解下t-SNE使用时有哪些坑,以及如何去避免犯这些错误。
可以用t-SNE来提出假设 不要用t-SNE得出结论
讲到这块的时候,Laurens说他参加顶会的时候喜欢四处逛逛,看到很多学术海报上数据可视化的部分用的正是t-SNE,虽然这个意味着又多了一个引用(偷笑),但是很遗憾,有些论文的用法是错误的,是他所不希望看到的。
比如他举了这样的一个例子,应该是NLP相关的论文,里面用t-SNE可视化了一些embedding出来,可以看到有一定类似语义迁移的规律,因此证明自己的方法是work的。但是很遗憾,这样做是错误的,因为如果把所有embedding同时乘以一个很大的数值,然后再用t-SNE做可视化,可以得到一个非常类似图。
Laurens强调,可以通过t-SNE的可视化图提出一些假设,但是不要用t-SNE来得出一些结论,想要验证你的想法,最好用一些其他的办法。
t-SNE中集群之间的距离并不表示相似度
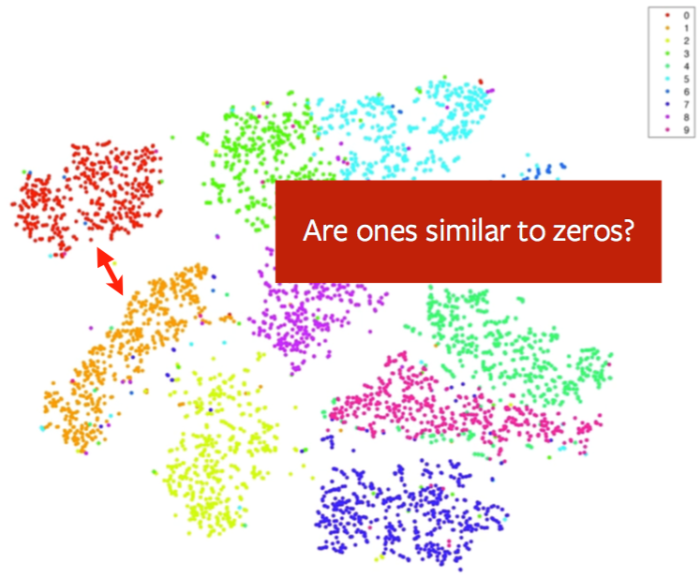
这一块可以通过那个经典的MNIST可视化出来的效果图进行说明,如果所示:
图中0和1的集群距离比较近,而0和7的集群距离较远,这说明0和1的相似度要更高吗?显然不是,事实上如果你在同一个数据上运行t-SNE算法多次,很有可能得到多个不同“形态”的集群,可能有的时候0和1集群比较近,可能0和8集群比较近。因此,考虑t-SNE可视化结果中不同集群之间的距离是没有意义的,因为对t分布来说,超出一定距离范围以后,其相似度都是很小的。也就是说,只要不在一个集群范围内,其相似度都是一个很小的值,我们所看到的集群之间的呈现出来的距离并不能说明什么,这是由t-SNE的内在所决定的。
t-SNE不能用于寻找离群点outlier
这一点同样要回到原来的论文中去,t-SNE是在SNE的基础上改进而来的,其中一个改进就是把SNE改成了对称的形式,如下所示:
\[p_{ij}=\frac {p_{j|i}+p_{i|j}}{2N}\]
原来的条件概率建模和KL距离都是非对称的,而在t-SNE中加了一个对称项,相当于在某种程度上把outlier拉进了某个集群。为什么呢?我们考虑一个离群点和一个集群的情况,只要perplexity设置的合理,那么在选择近邻时,集群内的点显然不会选择离群点作为自己的邻居,这在非对称的条件下是没什么问题的。而在对称的条件下,我们还要额外考虑离群点选择近邻的情况,由于它自身是离群点,那么它只能选择离它最近的集群中的点作为近邻。加入了这一项之后,我们相当于无形之中拉近了集群和离群点之间的距离,所得到的结果是有偏差的。所以t-SNE不能用来寻找离群点。
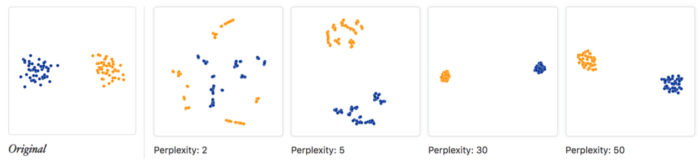
别忘了scale(perplexity)的作用
大部分人在使用t-SNE时,一般都直接使用默认参数图个方便(一般perplexity的默认值是30),如果忽视了perplexity带来的影响,有的时候遇到t-SNE可视化效果不好时,根本就不知道哪里出了问题,优化起来也就无从下手了。
那么perplexity到底是啥呢?我们可以回顾t-SNE的数学表达式,主要是和sigma这一项相关
perplexity表示了近邻的数量,例如设perplexity为2,那么就很有可能得到很多两个一对的小集群。
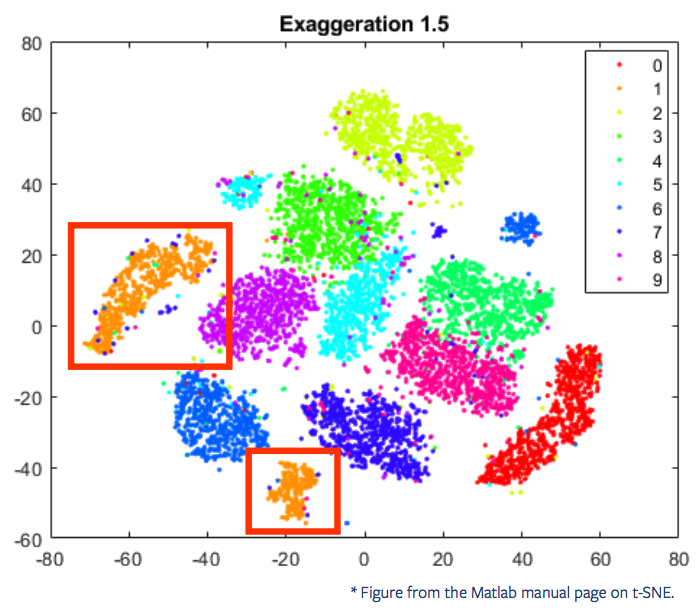
t-SNE是在优化一个non-convex目标函数,只是局部最小
会出现同一集群被分为两半的情况,如下图所示
正如刚才所说的,t-SNE更关心的是学习维持局部结构,群间的距离并不能说明什么,而且每次跑t-SNE的结果并不完全一致。所以解决这个问题,我们只需要跑多次找出效果最好的就可以了。引起这个问题的本质原因是,t-SNE是在优化一个非凸的目标函数,我们每次得到的只不过是一个局部最小。
低维度量空间不能capture非度量的相似性,有些高维结构(距离 相似性)特征在低维是无法反映出来的
这部分Laurens列举了一个他经常用的例子,也就是下图中的几个雕塑:
最左侧的是一个半人马雕塑,背上骑着一个小孩,我们可以说它和人相似,也可以它和马相似,但是我们是否能得出马和人相似的结论呢?显然是不能的。
这个例子想要表达的意思是,t-SNE终究只是一个把高维空间数据映射到低维的可视化工具,研究的也仅仅是低维流形上的数据特征,它不能表征那些非metric的相似性。有些仅在高维空间中存在的相似性,在低维流形上是没有办法表达出来的。
t-SNE is a valuable tool in generating hypotheses and understanding, but does not produce conclusive evidence
0x03 其他资源
这个网站不仅做了t-SNE可视化的例子,还有CNN可解释性的例子,可视化效果做的非常棒,强烈建议大家去尝试一下