数据降维与可视化之t-SNE

2017/01/12来源：hustqb评论5,420

t-SNE是目前来说效果最好的数据降维与可视化方法，但是它的缺点也很明显，比如：占内存大，运行时间长。但是，当我们想要对高维数据进行分类，又不清楚这个数据集有没有很好的可分性（即同类之间间隔小，异类之间间隔大），可以通过t-SNE投影到2维或者3维的空间中观察一下。如果在低维空间中具有可分性，则数据是可分的；如果在高维空间中不具有可分性，可能是数据不可分，也可能仅仅是因为不能投影到低维空间。
下面会简单介绍t-SNE的原理，参数和实例。

t-distributed Stochastic Neighbor Embedding(t-SNE)

t-SNE（TSNE）将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示，嵌入空间的相似度由“学生t分布”表示。

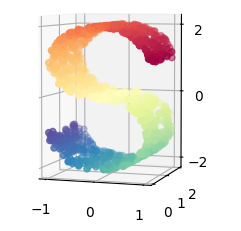
虽然Isomap，LLE和variants等数据降维和可视化方法，更适合展开单个连续的低维的manifold。但如果要准确的可视化样本间的相似度关系，如对于下图所示的S曲线（不同颜色的图像表示不同类别的数据），t-SNE表现更好。因为t-SNE主要是关注数据的局部结构。

通过原始空间和嵌入空间的联合概率的Kullback-Leibler（KL）散度来评估可视化效果的好坏，也就是说用有关KL散度的函数作为loss函数，然后通过梯度下降最小化loss函数，最终获得收敛结果。注意，该loss不是凸函数，即具有不同初始值的多次运行将收敛于KL散度函数的局部最小值中，以致获得不同的结果。因此，尝试不同的随机数种子(Python中可以通过设置seed来获得不同的随机分布)有时候是有用的，并选择具有最低KL散度值的结果。

使用t-SNE的缺点大概是：

t-SNE的计算复杂度很高，在数百万个样本数据集中可能需要几个小时，而PCA可以在几秒钟或几分钟内完成
Barnes-Hut t-SNE方法（下面讲）限于二维或三维嵌入。
算法是随机的，具有不同种子的多次实验可以产生不同的结果。虽然选择loss最小的结果就行，但可能需要多次实验以选择超参数。
全局结构未明确保留。这个问题可以通过PCA初始化点（使用init ='pca'）来缓解。

优化 t-SNE

t-SNE的主要目的是高维数据的可视化。因此，当数据嵌入二维或三维时，效果最好。有时候优化KL散度可能有点棘手。有五个参数可以控制t-SNE的优化，即会影响最后的可视化质量：

perplexity困惑度
early exaggeration factor前期放大系数
learning rate学习率
maximum number of iterations最大迭代次数
angle角度

Barnes-Hut t-SNE

Barnes-Hut t-SNE主要是对传统t-SNE在速度上做了优化，是现在最流行的t-SNE方法，同时它与传统t-SNE还有一些不同：

Barnes-Hut仅在目标维度为3或更小时才起作用。以2D可视化为主。
Barnes-Hut仅适用于密集的输入数据。稀疏数据矩阵只能用特定的方法嵌入，或者可以通过投影近似，例如使用sklearn.decomposition.TruncatedSVD
Barnes-Hut是一个近似值。使用angle参数对近似进行控制，因此当参数method="exact"时，TSNE()使用传统方法，此时angle参数不能使用。
Barnes-Hut可以处理更多的数据。 Barnes-Hut可用于嵌入数十万个数据点。

为了可视化的目的（这是t-SNE的主要用处），强烈建议使用Barnes-Hut方法。method="exact"时，传统的t-SNE方法尽管可以达到该算法的理论极限，效果更好，但受制于计算约束，只能对小数据集的可视化。

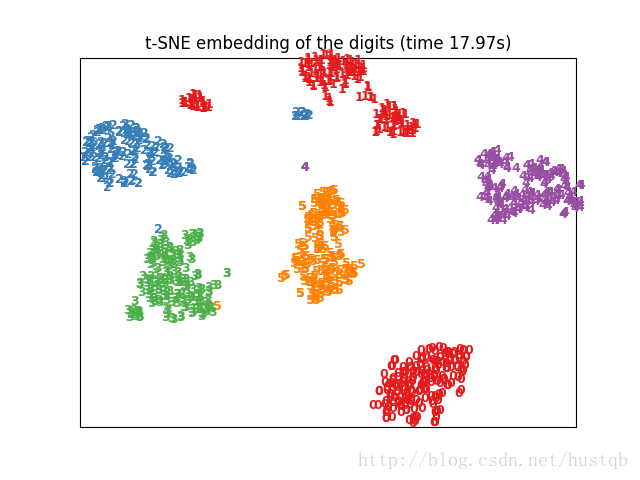
对于MNIST来说，t-SNE可视化后可以自然的将字符按标签分开，见本文最后的例程；而PCA降维可视化后的手写字符，不同类别之间会重叠在一起，这也证明了t-SNE的非线性特性的强大之处。值得注意的是：未能在2D中用t-SNE显现良好分离的均匀标记的组不一定意味着数据不能被监督模型正确分类，还可能是因为2维不足以准确地表示数据的内部结构。

注意事项

数据集在所有特征维度上的尺度应该相同

参数说明

parameters	description
n_components	int, 默认为2，嵌入空间的维度（嵌入空间的意思就是结果空间）
perplexity	float, 默认为30，数据集越大，需要参数值越大，建议值位5-50
early_exaggeration	float, 默认为12.0，控制原始空间中的自然集群在嵌入式空间中的紧密程度以及它们之间的空间。对于较大的值，嵌入式空间中自然群集之间的空间将更大。再次，这个参数的选择不是很关键。如果在初始优化期间成本函数增加，则可能是该参数值过高。
learning_rate	float, default:200.0, 学习率，建议取值为10.0-1000.0
n_iter	int, default:1000, 最大迭代次数
n_iter_without_progress	int, default:300, 另一种形式的最大迭代次数，必须是50的倍数
min_grad_norm	float, default:1e-7, 如果梯度低于该值，则停止算法
metric	string or callable, 精确度的计量方式
init	string or numpy array, default:”random”, 可以是’random’, ‘pca’或者一个numpy数组(shape=(n_samples, n_components)。
verbose	int, default:0, 训练过程是否可视
random_state	int, RandomState instance or None, default:None，控制随机数的生成
method	string, default:’barnes_hut’, 对于大数据集用默认值，对于小数据集用’exact’
angle	float, default:0.5, 只有`method='barnes_hut'`时可用

attributes	description
embedding_	嵌入向量
kl_divergence	最后的KL散度
n_iter_	迭代的次数

Methods	description
fit	将X投影到一个嵌入空间
fit_transform	将X投影到一个嵌入空间并返回转换结果
get_params	获取t-SNE的参数
set_params	设置t-SNE的参数

实例

Hello World

一个简单的例子，输入4个3维的数据，然后通过t-SNE降维称2维的数据。

import numpy as np
from sklearn.manifold import TSNE
X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
tsne = TSNE(n_components=2)
tsne.fit_transform(X)
print(tsne.embedding_)
'''输出
[[   3.17274952 -186.43092346]
 [  43.70787048 -283.6920166 ]
 [ 100.43157196 -145.89025879]
 [ 140.96669006 -243.15138245]]'''

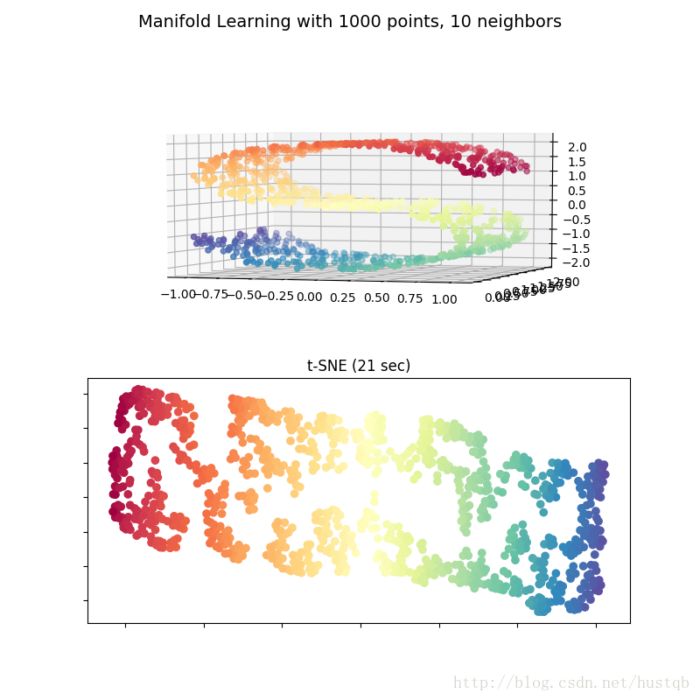
S曲线的降维与可视化

S曲线上的数据是高维的数据，其中不同颜色表示数据的不同类别。当我们通过t-SNE嵌入到二维空间中后，可以看到数据点之间的类别信息完美的保留了下来

# coding='utf-8'
"""# 一个对S曲线数据集上进行各种降维的说明。"""
from time import time
 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
 
from sklearn import manifold, datasets
 
# # Next line to silence pyflakes. This import is needed.
# Axes3D
 
n_points = 1000
# X是一个(1000, 3)的2维数据，color是一个(1000,)的1维数据
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
n_components = 2
 
fig = plt.figure(figsize=(8, 8))
# 创建了一个figure，标题为"Manifold Learning with 1000 points, 10 neighbors"
plt.suptitle("Manifold Learning with %i points, %i neighbors"
             % (1000, n_neighbors), fontsize=14)
 
 
'''绘制S曲线的3D图像'''
ax = fig.add_subplot(211, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
ax.view_init(4, -72)  # 初始化视角
 
'''t-SNE'''
t0 = time()
tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
Y = tsne.fit_transform(X)  # 转换后的输出
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0))  # 算法用时
ax = fig.add_subplot(2, 1, 2)
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral)
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
ax.xaxis.set_major_formatter(NullFormatter())  # 设置标签显示格式为空
ax.yaxis.set_major_formatter(NullFormatter())
# plt.axis('tight')
 
plt.show()

手写数字的降维可视化

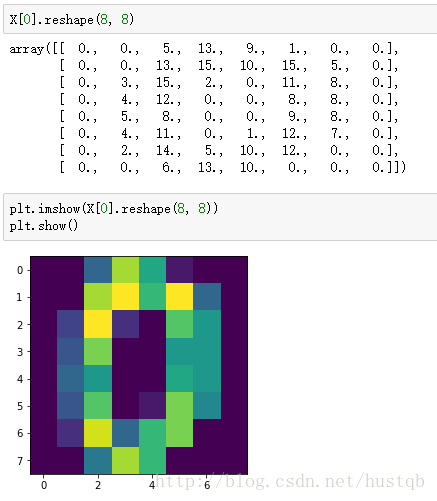
这里的手写数字数据集是一堆8*8的数组，每一个数组都代表着一个手写数字。如下图所示。

t-SNE将8*8即64维的数据降维成2维，并在平面图中显示，这里只选取了0-5，6个手写数字。

# coding='utf-8'
"""t-SNE对手写数字进行可视化"""
from time import time
import numpy as np
import matplotlib.pyplot as plt
 
from sklearn import datasets
from sklearn.manifold import TSNE
 
 
def get_data():
    digits = datasets.load_digits(n_class=6)
    data = digits.data
    label = digits.target
    n_samples, n_features = data.shape
    return data, label, n_samples, n_features
 
 
def plot_embedding(data, label, title):
    x_min, x_max = np.min(data, 0), np.max(data, 0)
    data = (data - x_min) / (x_max - x_min)
 
    fig = plt.figure()
    ax = plt.subplot(111)
    for i in range(data.shape[0]):
        plt.text(data[i, 0], data[i, 1], str(label[i]),
                 color=plt.cm.Set1(label[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})
    plt.xticks([])
    plt.yticks([])
    plt.title(title)
    return fig
 
 
def main():
    data, label, n_samples, n_features = get_data()
    print('Computing t-SNE embedding')
    tsne = TSNE(n_components=2, init='pca', random_state=0)
    t0 = time()
    result = tsne.fit_transform(data)
    fig = plot_embedding(result, label,
                         't-SNE embedding of the digits (time %.2fs)'
                         % (time() - t0))
    plt.show(fig)
 
 
if __name__ == '__main__':
    main()