1. 从意义上看:
- 指数分布解决的问题是“要等到一个随机事件发生,需要经历多久时间”
- 伽玛分布解决的问题是“要等到n个随机事件都发生,需要经历多久时间”
所以,伽玛分布可以看作是n个指数分布的独立随机变量的加总,即,n个Exponential(λ)random variables--->Gamma(n,λ)
- 泊松分布解决的是“在特定时间里发生n个事件的机率”。
2. 公式
- 泊松分布
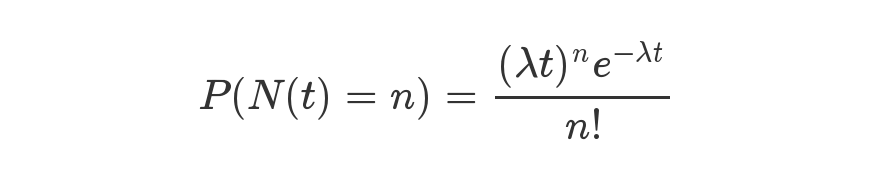
上面就是泊松分布的公式。等号的左边,P 表示概率,N表示某种函数关系,t 表示时间,n 表示数量,1小时内出生3个婴儿的概率,就表示为 P(N(1) = 3) 。等号的右边,λ 表示事件的频率。
- 接下来两个小时,一个婴儿都不出生的概率是0.25%,基本不可能发生。
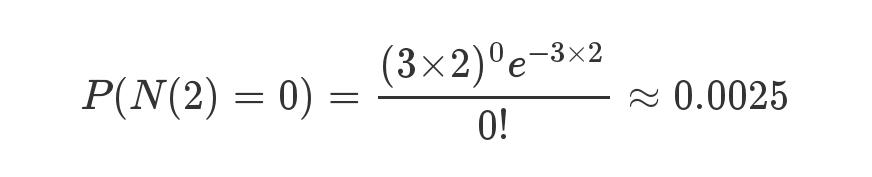
- 接下来一个小时,至少出生两个婴儿的概率是80%。
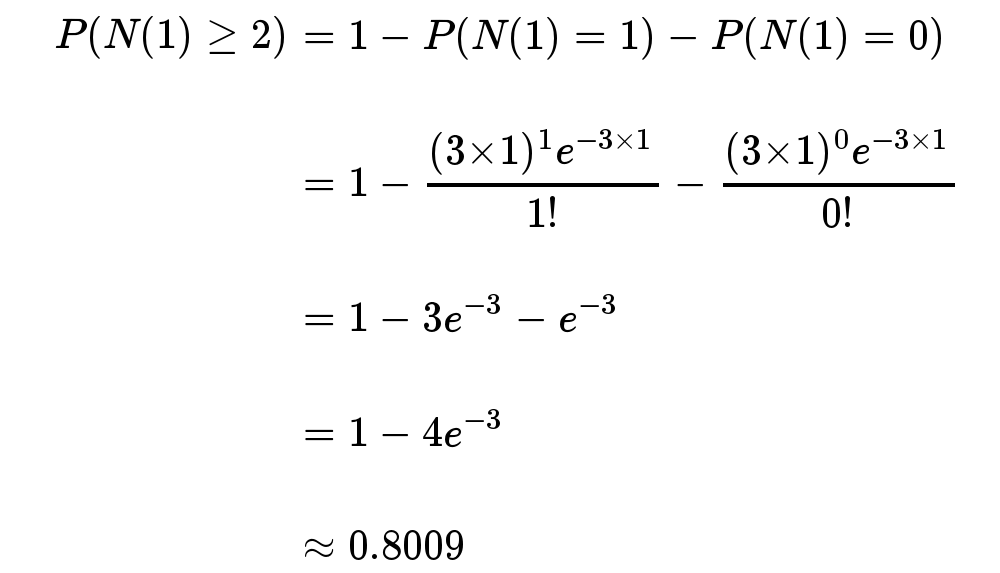
- 泊松分布的图形
- 指数分布
- 指数分布解决的问题是“要等到一个随机事件发生,需要经历多久时间”
- 指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ,就等同于 t 之内没有任何婴儿出生。
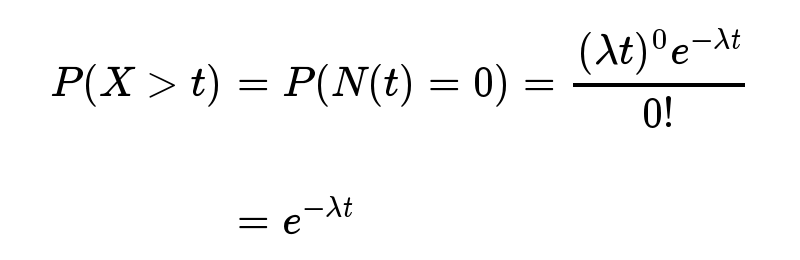
- 反过来,事件在时间 t 之内发生的概率,就是1减去上面的值。
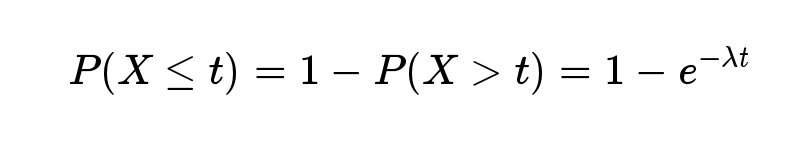
- 接下来15分钟,会有婴儿出生的概率是52.76%。
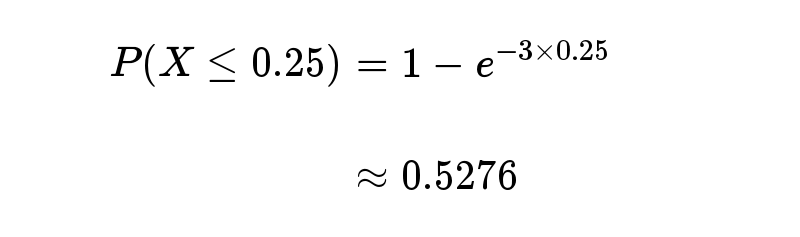
- 接下来的15分钟到30分钟,会有婴儿出生的概率是24.92%。
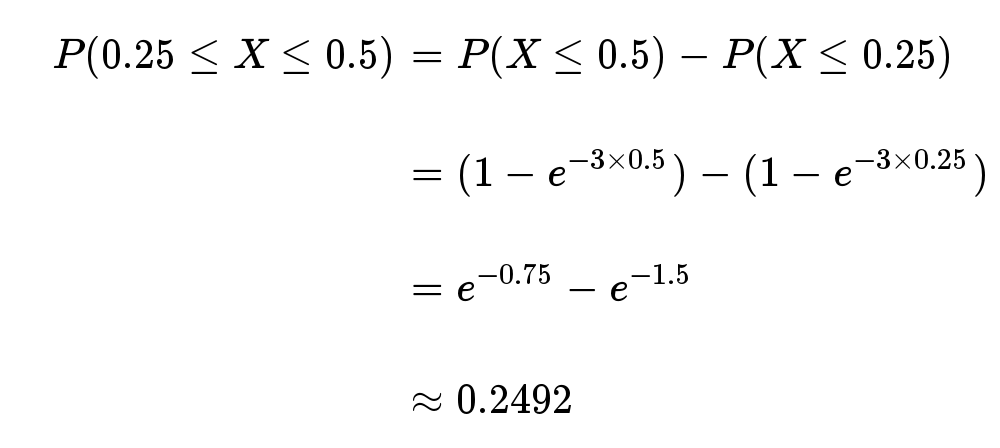
- 指数分布的图形
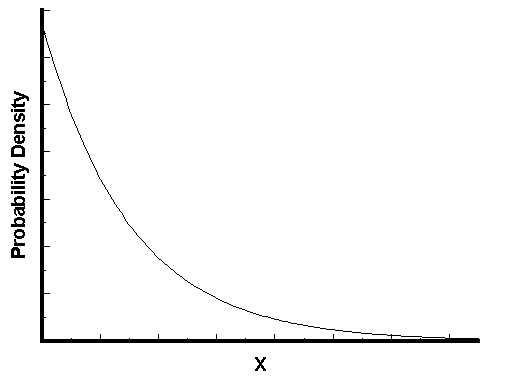
可以看到,随着间隔时间变长,事件的发生概率急剧下降,呈指数式衰减。想一想,如果每小时平均出生3个婴儿,上面已经算过了,下一个婴儿间隔2小时才出生的概率是0.25%,那么间隔3小时、间隔4小时的概率,是不是更接近于0?
- 伽马分布
- 伽玛分布解决的问题是“要等到n个随机事件都发生,需要经历多久时间”
- 公式
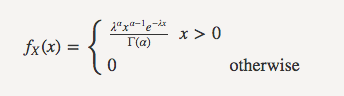
这里a=n, 当a=1时,伽马分布就是指数分布,所以伽马分布就是n个指数分布的和
- 期望和方差
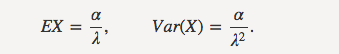
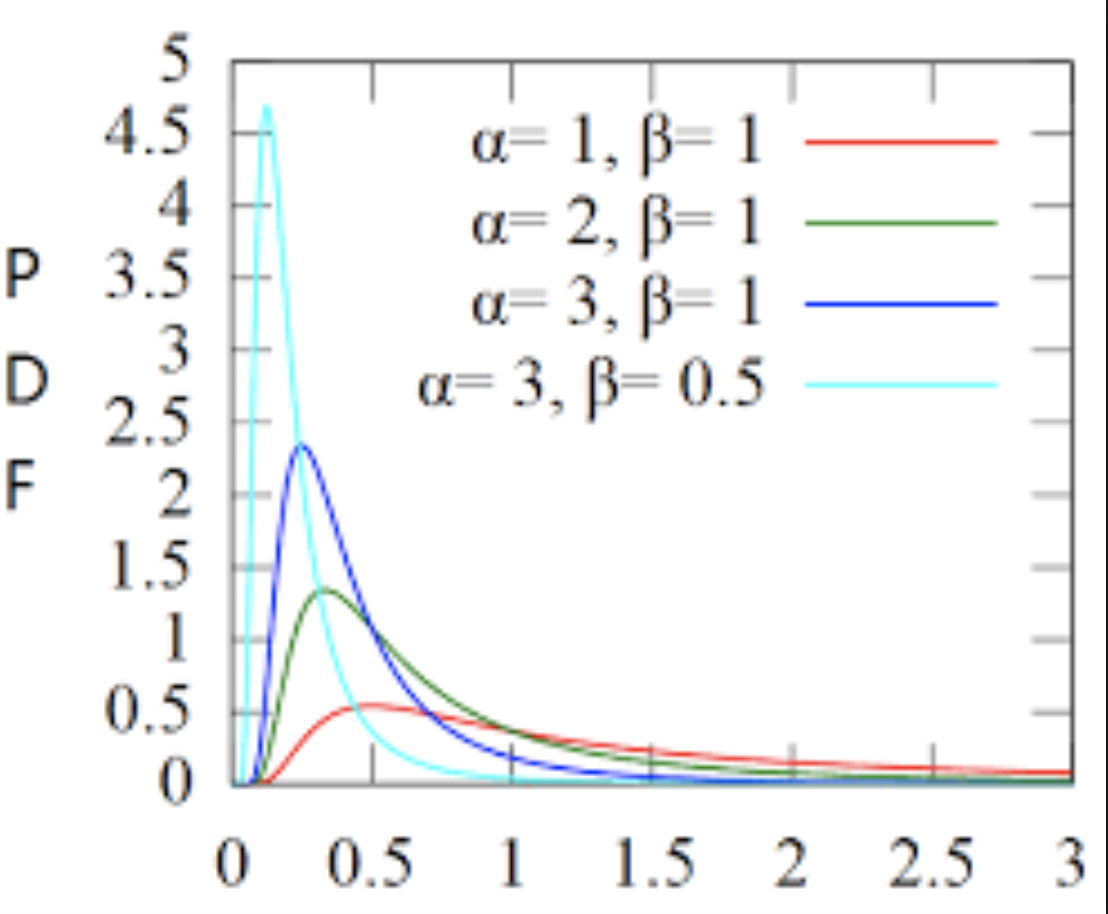
- Gamma分布中的参数α称为形状参数(shape parameter),β称为尺度参数(scale parameter)。
参考
- https://www.zhihu.com/question/34866983
- http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html


