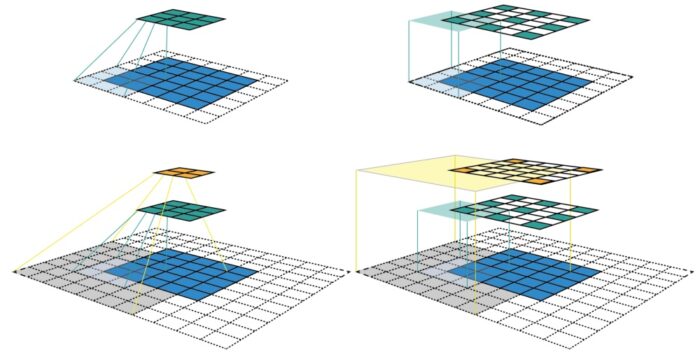
0. Calculating Receptive Field of CNN
感受野指的是一个特定的 CNN 特征(特征图上的某个点)在输入空间所受影响的区域。一个感受野可以用中信位置和打表来表征。然而,对于一个 CNN 特征来说,感受野中的每一个像素值并不是同等重要。一个像素点越接近感受野中心,它对输出特征的计算所起作用越大。这意味着某一个特征不仅仅是受限在输入图片中某个特定的区域(感受野),并且呈指数级聚焦在区域的中心。感受野的计算公式如下:
$$l_{k} = l_{k-1}+ \left [ (f_{k}-1)*\prod_{i=1}^{k-1}s_{i} \right ]$$
其中 $l_{k-1}$ 为第 $k-1$ 层对应的感受野大小,$f_k$ 为第 $k$ 层的卷积核大小,或者是池化层的池化尺寸大小。
更为细致的解释如下:
The receptive field (RF) lk of layer k is:
$l_{k} = l_{k-1}+ \left [ (f_{k}-1)*\prod_{i=1}^{k-1}s_{i} \right ]$
where $l_{k-1}$ is the receptive field of layer $k−1$, $f_k$ is the filter size (height or width, but assuming they are the same here), and $s_i$ is the stride of layer $i$.
The formula above calculates receptive field from bottom up (from layer 1). Intuitively, RF in layer k covers $(f_k−1)∗s_{k−1}$ more pixels relative with layer $k−1$. However, the increment needs to be translated to the first layer, so the increments is a factorial — a stride in layer $k−1$ is exponentially more strides in the lower layers.
1. 举个例子
感受野的计算是逐层进行的,以下表中的网络结构为例。
| No. | Layers | Kernel Size | Stride |
|---|---|---|---|
| 1 | Conv1 | 3*3 | 1 |
| 2 | Pool1 | 2*2 | 2 |
| 3 | Conv2 | 3*3 | 1 |
| 4 | Pool2 | 2*2 | 2 |
| 5 | Conv3 | 3*3 | 1 |
| 6 | Conv4 | 3*3 | 1 |
| 7 | Pool3 | 2*2 | 2 |
感受野初始值 $l_0 = 1$,每层的感受野计算过程如下:
$l_0 = 1$
$l_1 = 1 + (3-1) = 3$
$l_2 = 3 + (2-1)*1 = 4$
$l_3 = 4 + (3-1)*1*2 = 8$
$l_4 = 8 + (2-1)*1*2*1 = 10$
$l_5 = 10 + (3-1)*1*2*1*2 = 18$
$l_6 = 18 + (3-1)*1*2*1*2*1 = 26$
$l_7 = 26 + (2-1)*1*2*1*2*1*1 = 30$