题记:本文成形于2015年并于2017年收录于由笔者与胡志德医生共同主编,中南大学出版社出版的《疯狂统计学》,此次属旧文重发,较原文有所改动。
1. 背景知识
多元线性回归、Logistic回归和Cox回归是医学统计分析中使用最多的三种回归方法,关于这三种回归方法的原理、统计软件操作、结果解读我们在《聪明统计学》中已经做了较为详细的介绍[1],但其中关于多因素回归变量筛选的方法并未做重点介绍,而这个问题又是许多临床医生在论文写作中感到困惑的地方。当临床医生感到困惑时往往会求助统计学家,而统计学家很多时候给到的答案是:我们可以借助统计软件的变量筛选方法自动实现变量筛选,因为SPSS软件中在Logistic回归和Cox回归中给出了7种变量筛选的方法[2]:
① 条件参数估计似然比检验(向前:条件);
② 最大偏似然估计的似然比检验(向前:LR);
③ Wald卡方检验(向前:Wald);
④ 条件参数估计似然比检验(向后:条件);
⑤ 最大偏似然估计的似然比检验(向后:LR);
⑥ Wald卡方检验(向后:Wald);
⑦ Enter法(变量全部进入)。现实情况是,我们在读临床文献的时候,很多作者采用下面一种变量筛选的方法:首先逐个对变量进行单因素回归分析,把单因素回归分析P值小于0.1的纳入最终的回归方程(此处变量筛选的标准也可把P值设为0.05或0.2,一般不会设置小于0.05,也不会设置大于0.2)。
这两种方法到底该如何选择呢?坦率的讲,这个问题没有标准答案。但笔者认为变量筛选应该考虑以下几条基本原则:第一种情况,当有效样本量很大,统计学检验效能足够的时候,可以使用上述6种变量自动筛选的方法中的任何一种。这里有一个经验性的判断统计学效能是否足够的标准:即一个单变量因素至少有20个有效样本量,举例来说,比如我们做Cox回归分析,如果我们收集了10个与预后相关的变量,那么至少应该有200个患者出现了我们定义的终点事件,比如死亡,此处需要注意的是至少200个死亡患者,而非200个患者,未出现终点事件的样本我们一般不把其视为有效样本。第二种情况,当不满足上述条件,或者其他原因导致的统计学效能不够的情况,应该采用大多数临床研究报告中采用的变量筛选方法,即首先逐个对变量进行单因素回归分析,把单因素回归分析P值小于0.1的纳入最终的回归方程。这种方法虽然广泛使用,但也饱受统计学家的质疑。第三种情况,即便是第二种方法,也未必可以“高枕无忧”了,有时我们会发现某些确定与某种疾病临床预后相关的变量,在单因素分析的时候并未达到我们所设定的变量筛选标准,而被排除在多因素回归模型之外,比如在一个前列腺癌预后因素分析的研究中,作者并未发现Gleason评分与预后显著相关,而临床上比较肯定的是Gleason评分与前列腺癌患者的预后显著相关,此时我们应该怎样做出取舍呢?笔者认为,对于那些已知的确定与某疾病预后显著相关的变量,即便未达到我们设定的统计学筛选标准,我们也应该纳入回归模型,这么做的考量即是从临床专业角度筛选变量。综上,笔者推荐第三种变量筛选的方法,统筹考虑统计学上的单因素分析结果与已知临床专业知识决定纳入回归方程的变量。
下面我们就以案例的形式为大家演示多因素回归中变量筛选的操作过程,为了便于读者阅读,我们首先以上述第二种方法为变量筛选的原则。[案例1]的数据下载自TheCancer Genome Atlas(TCGA)数据库,经整理后获得。为了便于读者阅读和练习模仿,笔者对数据进行了简化处理。
2. 案例与软件操作
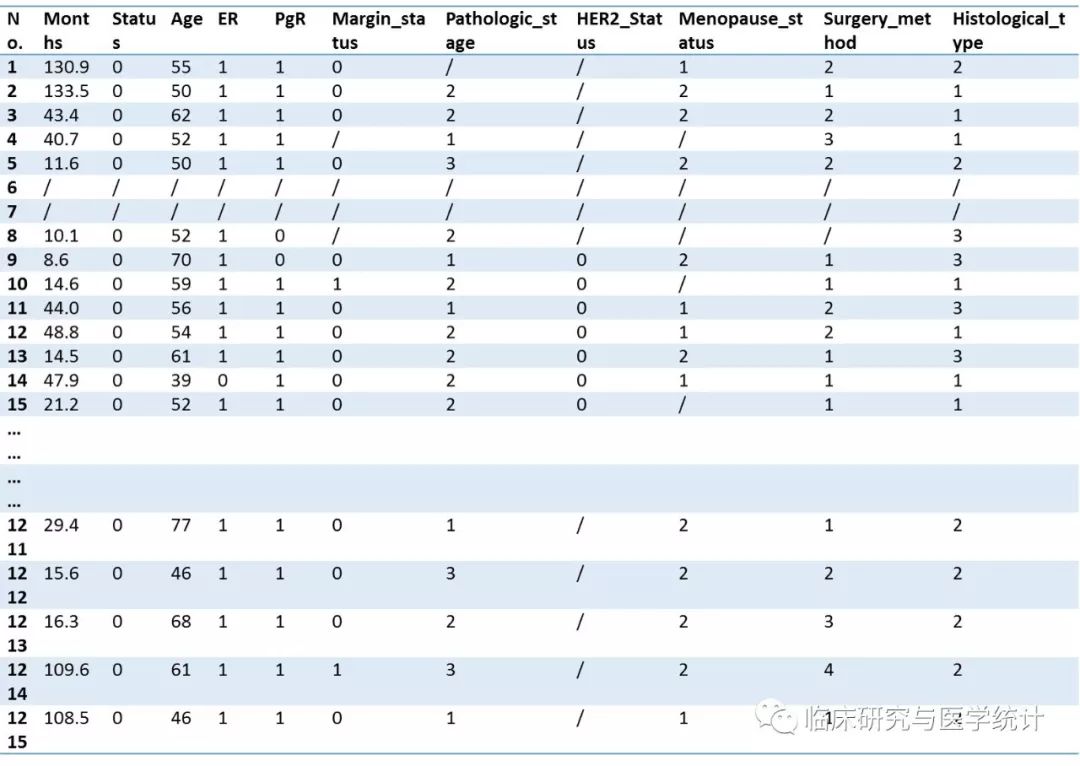
[案例1] 笔者在TheCancer Genome Atlas(TCGA)数据中下载了1215例乳腺癌的临床资料及预后信息。下载网址:https://genome-cancer.ucsc.edu/。数据经整理后如下表1所示,变量定义及赋值说明如表2所示。这是一个生存资料,我们的研究目的就是要观察这1215例乳腺癌患者的独立预后因素是哪些?此处需要说明的是,影响乳腺癌患者预后的因素可能很多,囿于客观条件我们无法对所有可能变量进行收集,到底该采集哪些变量,这是试验设计阶段该考虑的问题,一般来说变量收集的范围大致包括以下几个方面:第一,人口学特征,比如年龄、性别、种族等;第二,疾病本身的特点,比如疾病的严重程度,病理组织学类型、基因表达信息等;第三,与治疗相关的变量,比如既往接受过的治疗方式,是否手术,是否药物治疗,目前接受治疗的状况、给药剂量等。本案例中,我们为了简化问题使其更具有代表性,我们仅收集了9个可能影响预后的变量,大体上涵盖了上述三种情况。
表1. 1215例乳腺癌患者的生存资料
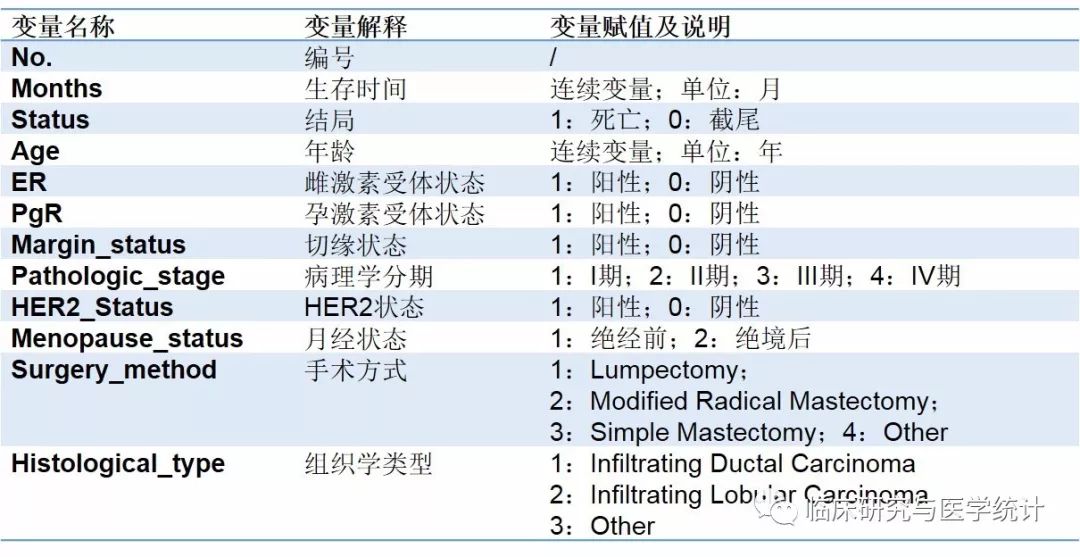
表2. 变量定义、赋值及说明
下面我们就以本案例中的数据演示Cox回归中变量筛选的实践操作过程。首先把表1所示的使用Excel整理好的数据导入IBM SPSS 22.0(IBM SPSS, NY, USA)软件中。接下来对收集的9个变量逐个做单因素Cox回归分析,我们设定变量筛选标准为 α=0.1,即单因素Cox回归分析P<0.1的变量纳入最终多因素Cox回归分析。本例中总计有9个变量,有连续变量,有二分类变量,有等级资料和无序分类资料,前两种变量类型的处理方式类似,等级资料和无序分类资料需要设置哑变量。下面我们分别选择一种类型的变量进行演示。
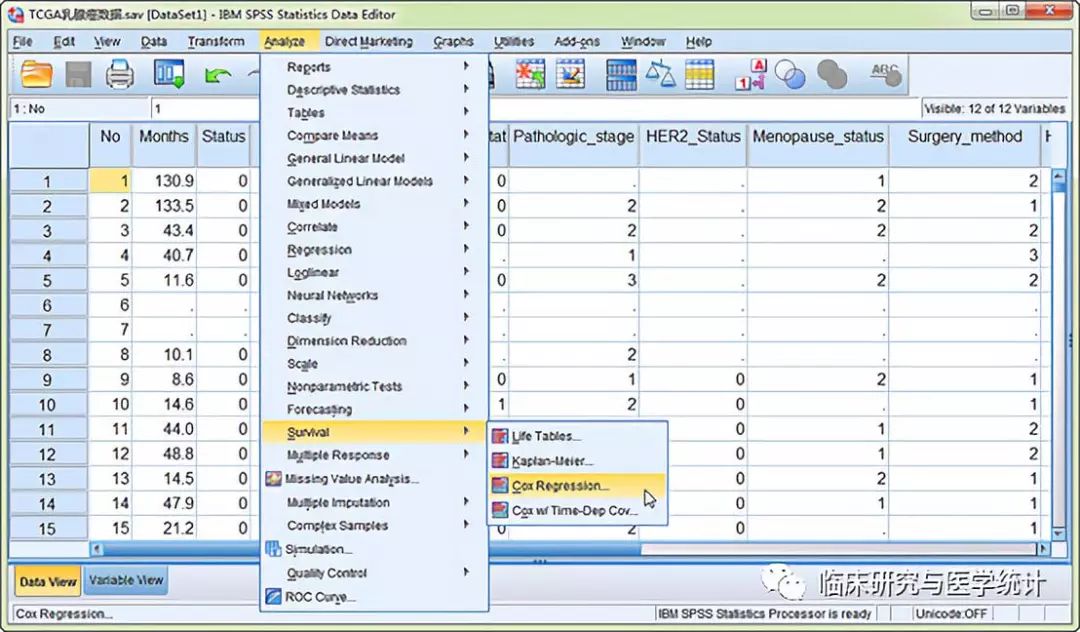
图1. 单因素Cox回归分析,依次选择 “Analyze” “Survival” “Cox Regression”。
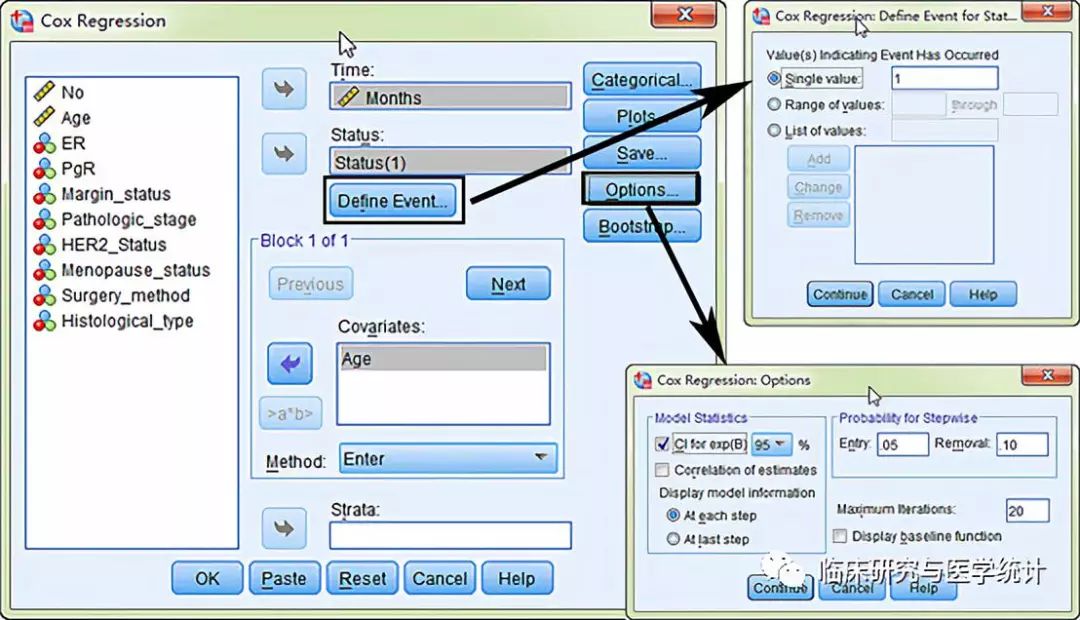
图2. 单因素Cox回归分析,依次如图所示选择:变量“Months”选入“Time”框中变量“Status”选入“Status” 框中“Define Event”变量“Age” 选入“Covariate”框中“Options”勾选95%可信区间。此处变量“Age”为连续变量。
图3. 单因素Cox回归分析结果,P=0.0000.1,符合我们设定的筛选标准,纳入多因素回归模型。此处的Exp(B)即风险比(HR),HR=1.026表示年龄每增长1个单位,死亡风险增加2.6%,或者说年龄50岁患者的死亡风险是49岁的1.026倍。
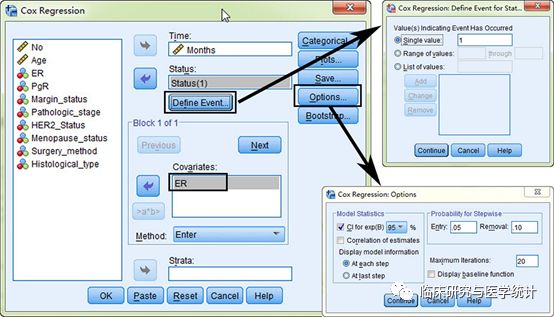
图4. 单因素Cox回归分析,依次选择 “Analyze” “Survival” “Cox Regression”。依次如图所示选择:变量“Months”选入“Time”框中→变量“Status”选入“Status” 框中→“Define Event”→变量“ER” 选入“Covariate”框中→“Options”勾选95%可信区间。此处“ER”为二分类变量。
图5. 单因素Cox回归分析结果,P=0.1540.1,根据我们设定的筛选标准,此变量不能纳入多因素回归模型。此处的Exp(B)即风险比(HR),HR=0.778表示ER阳性患者的死亡风险是ER阴性的0.778倍,但未达到统计学假设检验的阳性。
图6. 单因素Cox回归分析结果,P=0.0640.1,根据我们设定的筛选标准,此变量纳入多因素回归模型。此处的Exp(B)即风险比(HR),HR=0.740表示PgR阳性患者的死亡风险是PgR阴性的0.740倍。
图7. 单因素Cox回归分析结果,P=0.0720.1,根据我们设定的筛选标准,此变量纳入多因素回归模型。此处的Exp(B)即风险比(HR),HR=1.594表示切缘阳性患者的死亡风险是切缘阴性的1.594倍。
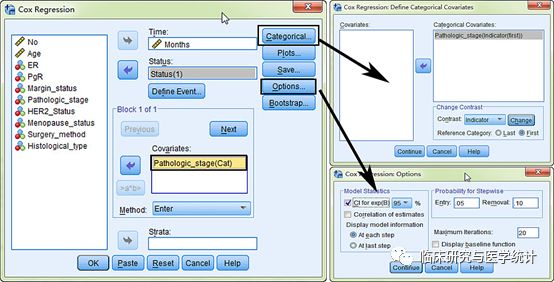
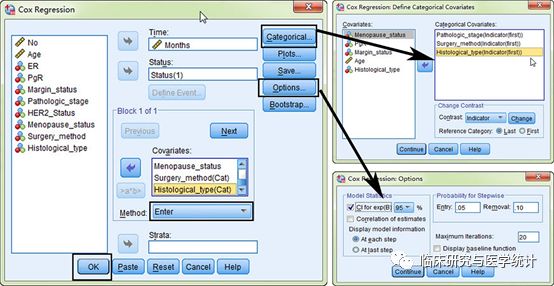
图8. 单因素Cox回归分析,依次选择 “Analyze”“Survival”“Cox Regression”。依次如图所示选择:变量“Months”选入“Time”框中 → 变量“Status”选入“Status” 框中 → “Define Event” → 变量“Pathologic_stage” 选入“Covariate”框中“Categorical”设置哑变量,把 “Pathologic_stage” 选入 “Categorical Covariate” 框中, “Options” 勾选95%可信区间。此处变量“Pathologic_stage”为等级变量。无序多分类变量的处理原则与此相同。
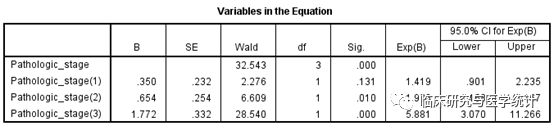
图9. 单因素Cox回归分析结果,P=0.0000.1,根据我们设定的筛选标准,此变量纳入多因素回归模型。此处分别给出Pathologic_stage(1),Pathologic_stage(2),Pathologic_stage(3)的Exp(B)即风险比(HR),HR分别为1.419、1.923、5.881,前一步骤中设置 “First”为参照,即设置病理分期的“I期”为参照,则Pathologic_stage(1),Pathologic_stage(2), Pathologic_stage(3)分别表示II期 vs. I期、III期 vs. I期、IV期 vs. I期,哑变量设置的目的即是指定一个参照。
图10. 单因素Cox回归分析结果,不纳入多因素Cox回归,结果解读略。
图11. 单因素Cox回归分析结果,纳入多因素Cox回归,结果解读略。
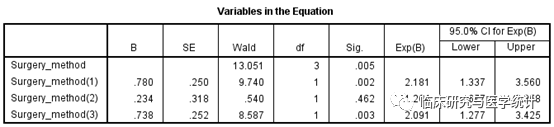
图12. 单因素Cox回归分析结果,纳入多因素Cox回归,结果解读略。
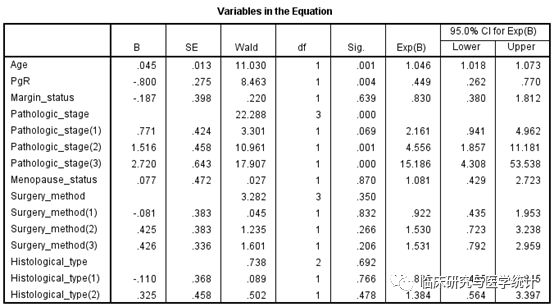
图13. 单因素Cox回归分析结果,纳入多因素Cox回归,此处是多分类变量,其中任意一个比较的P值小于0.1即应该纳入回归方程。结果解读略。至此9个变量的单因素分析已经完毕,我们把需要纳入最后的回归方程的变量挑出来。
图14. 多因素Cox回归分析结果。把单变量Cox回归分析筛选的变量选入“Covariates”框中选择默认的“Enter”发,即所有变量均进入回归方程。无序多分类变量及等级资料设置哑变量,勾选HR的95%可信区间。
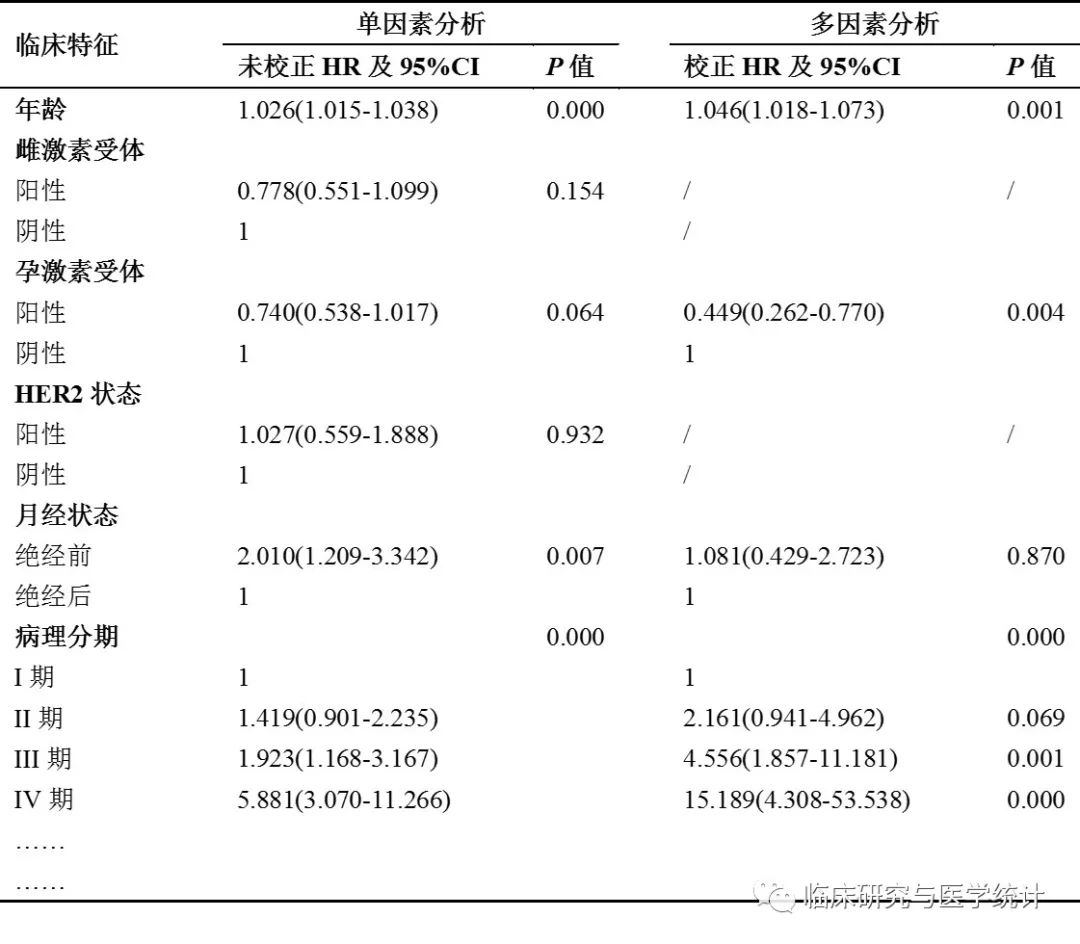
图15. 最终的多因素Cox回归分析结果。此结果表中P0.05的即是独立的影响预后的因素,由此可以看出本例中变量Age、PgR、Pathologic_stage是影响乳腺癌患者的独立预后因素。以上单因素与多因素分析的结果加以整理后在论文中报告中即可,可参见下表范式。
表3.单因素分析与多因素分析结果报告范式
3. 总结与讨论
综上,我们以生存资料为例演示了Cox回归中变量筛选的方法,多因素Logistic回归与多元线性回归的的变量筛选方法与上述Cox回归方法相同,我们不再演示其操作过程。在上述操作过程中,我们并未从临床专业角度考虑变量的取舍,众所周知ER与乳腺癌患者的预后相关,但本例中单因素Cox回归分析中变量ER的P值为0.154,并未达到我们设定的筛选标准,并未进入最终的回归模型,这种做法是否妥当?正如前文所述,我们也可以兼顾临床专业考虑与统计学考量决定最终纳入回归模型的变量,即便不符合我们设定的变量筛选标准,也将其纳入最终的回归模型进项校正。当然作者也可以尝试按照不同的变量筛选原则构建多个回归模型,通过回归模型诊断、预测效能评价等统计学方法比较不同回归模型的优劣,比如计算不同回归模型的C-Index或者C-Statistic等,有关C-Index的计算方法在本书Nomogram绘制的相关章节有详细介绍,感兴趣的读者可以尝试。对于大多数的临床医生来说,可能并不需要那么高深的统计学方法,如果可以掌握本文中所描述的变量筛选方法即可满足我们大部分的临床需求。
4. 参考文献
[1]. 周支瑞,胡志德.聪明统计学. 长沙:中南大学出版社, 2016.
[2]. 张文彤主编.SPSS统计分析高级教程. 北京:高等教育出版社, 2004.
[3]. 周支瑞,胡志德.疯狂统计学. 长沙:中南大学出版社, 2016.