1. 背景介绍
人们对于“算命”这样的事情总是乐此不彼,无论是中国文化中“算命占卜”还是西方文化中的“占星术”,无不说明人们对于此道的热衷。本章讨论的构建预测模型也是一种“算命”,只是这是一种更为科学的“算命”。作为一个肿瘤科医生,临床上可能会遇到这样的情况,一个55岁男性中晚期食管癌患者问道:医生,请问我还能活多久?大多数时候我们会根据患者的临床分期告诉患者,这种情况的中位生存时间是多少……其实这里的临床分期就是我们预测患者期望寿命的依据,或者如本文标题所说的“预测模型”,我们用某一临床分期的所有患者中位生存时间来回答单个患者的问题,可能会存在问题,这里的中位生存时间代表的是患病人群预期寿命的平均值,对于具体的个体来说有时并不准确。
那我们是否有更科学、更准确的方法计算出单个患者的生存概率?答案是肯定的。我们可以通过Cox回归等方法先构建一个数学模型,然后把这个模型可视化为Nomogram,通过图形来计算每个具体患者的生存概率。Nomogram中文常称为诺莫图或者列线图,其本质就是回归方程的可视化。它根据所有自变量标准回归系数的大小来制定评分标准,给每个自变量的每种取值水平一个评分,对每个患者,就可计算得到一个总分,再通过得分与结局发生概率之间的转换函数来计算每个患者的结局时间发生的概率。举例来说,我们治疗了一个40岁的男性胰腺癌手术后的患者,术中进行了放疗,肿瘤位于胰腺头部,有腹膜转移,临床分期在IV期。根据上述条件,通过一定的数学模型判断每个变量的得分,比如年龄40岁,得分是10分,男性得分是4分……依次累计各个变量的得分,计算出总分,不同的总分值就对应3月、6月和1年的生存概率。复杂的Cox回归公式变成了直观的图片,医生可以很方便的计算每个患者的生存概率,从而告知患者一个相对准确的“算命”结果。模型预测是否准确,一致性好不好等概念我们将在后续文章中陆续介绍。
2. 案例与操作
本章我们以[案例 1]的数据,介绍生存资料预后模型的建立与Nomogram图形绘制。为了便于读者阅读与练习模仿,笔者对数据进行了简化处理。
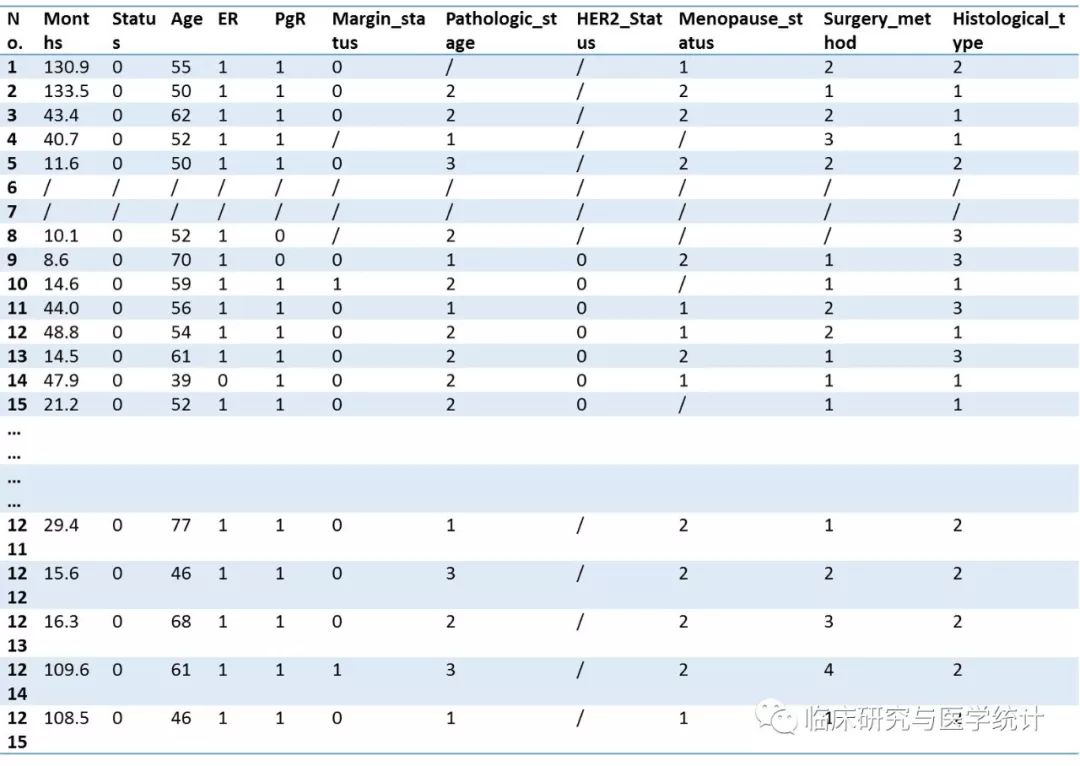
[案例 1] 笔者在The Cancer Genome Atlas (TCGA) 数据中下载1215例浸润性乳腺癌患者的临床资料。下载网址: https://genome-cancer.ucsc.edu/。数据经整理后如下 表1 所示,变量定义及赋值说明如表2所示。研究目的就是要根据1215例乳腺癌患者的生存资料构建预测模型并绘制 Nomogram。
表1. 1215例乳腺癌患者的生存资料
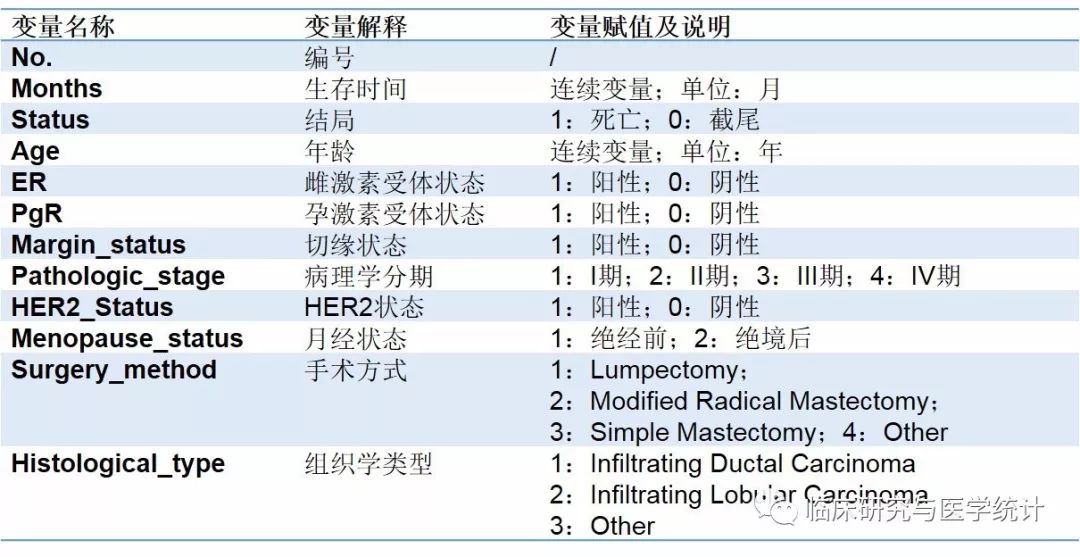
表2.变量定义、赋值及说明
步骤 1. 我们首先使用Cox回归基于构建预测模型并筛选独立预后因素(用于建模的数据集一般称为训练集或者内部数据集)。需要说明的是本例的数据录入、单因素Cox回归分析,多因素Cox回归分析等操作可参考笔者主编的《聪明统计学》[1] 与《疯狂统计学》[2]。最终我们可得到三个与预后相关的独立因素:Age, PgR, Pathologic_stage。
步骤 2. 我们就以这三个独立的预后因素绘制Nomogram,建模完成。
步骤 3. 对上述两步所构建的预测模型的区分能力 (Discrimination) 进行评价,并计算C-index。
步骤 4. 对模型进行验证,可通过外部数据集进行验证,如果无法获得外部数据集,笔者推荐采用Bootstrap冲抽样法基于训练集验证模型并绘制校正曲线(Calibration plot)。
3. 计算过程
我们重点讲解Cox回归模型中C-Index计算,Nomogram绘制过程,Bootstrap法验证模型及绘制标准曲线。以下所有操作均基于R软件,软件下载地址:https://www.r-project.org/. 我们把数据另存为BreastCancer.sav,并保存至R的当前工作目录下。计算结果如图1及图2所示。
载入程序包
- library(foreign)library(rms)
- ## Loading required package: Hmisc
- ## Loading required package: lattice
- ## Loading required package: survival
- ## Loading required package: Formula
- ## Loading required package: ggplot2
- ##
- ## Attaching package: 'Hmisc'
- ## The following objects are masked from 'package:base':
- ##
- ## format.pval, units
- ## Loading required package: SparseM
- ##
- ## Attaching package: 'SparseM'
- ## The following object is masked from 'package:base':
- ##
- ## backsolve
数据准备
读入.sav格式的数据
- breast<-read.spss("BreastCancer.sav")
把数据转换为数据框格式
- breast<-as.data.frame(breast)
- breast<-na.omit(breast)
展示数据框的前6行数据
- head(breast)
- ## No Months Status Age ER PgR Margin_status
- ## 9 9 8.633333 Censor 70 Positive Negative Nagative
- ## 11 11 44.033333 Censor 56 Positive Positive Nagative
- ## 12 12 48.766667 Censor 54 Positive Positive Nagative
- ## 13 13 14.466667 Censor 61 Positive Positive Nagative
- ## 14 14 47.900000 Censor 39 Negative Positive Nagative
- ## 19 19 39.866667 Censor 50 Positive Positive Nagative
- ## Pathologic_stage HER2_Status Menopause_status
- ## 9 Stage I Negative Post menopause
- ## 11 Stage I Negative Pre menopause
- ## 12 Stage II Negative Pre menopause
- ## 13 Stage II Negative Post menopause
- ## 14 Stage II Negative Pre menopause
- ## 19 Stage II Positive Post menopause
- ## Surgery_method Histological_type
- ## 9 Lumpectomy Other
- ## 11 Modified Radical Mastectomy Other
- ## 12 Modified Radical Mastectomy Infiltrating Ductal Carcinoma
- ## 13 Lumpectomy Other
- ## 14 Lumpectomy Infiltrating Ductal Carcinoma
- ## 19 Lumpectomy Infiltrating Ductal Carcinoma
定义终点事件
- breast$Status<-ifelse(breast$Status=="Dead",1,0)
设置参考组
- breast$Pathologic_stage<- relevel(breast$Pathologic_stage,ref='Stage I')
构建Cox回归方程
- coxm <-cph(Surv(Months,Status==1)~Age+Pathologic_stage+PgR,x=T,y=T,data=breast,surv=T)
- surv<- Survival(coxm) # 建立生存函数
- surv1<- function(x)surv(1*12,lp=x) # 定义time.inc,1年OS
- surv2<- function(x)surv(1*36,lp=x) # 定义time.inc,3年OS
- surv3<- function(x)surv(1*60,lp=x) # 定义time.inc,5年OS
- dd<-datadist(breast) # 将数据整合
- options(datadist='dd') # 将数据整合
绘制列线图。maxscale参数指定最高分数,一般设置为100或者10分;un.at 设置生存率的刻度;xfrac 设置数值轴与最左边标签的距离,可以调节下数值观察下图片变化情况
- plot(nomogram(coxm,fun=list(surv1,surv2,surv3),lp=F,funlabel=c("1-Yeas OS", '3-Year OS','5-YearOS'),maxscale=100,fun.at=c('0.95','0.85','0.80','0.70','0.6','0.5','0.4','0.3','0.2','0.1')),xfrac=.3)
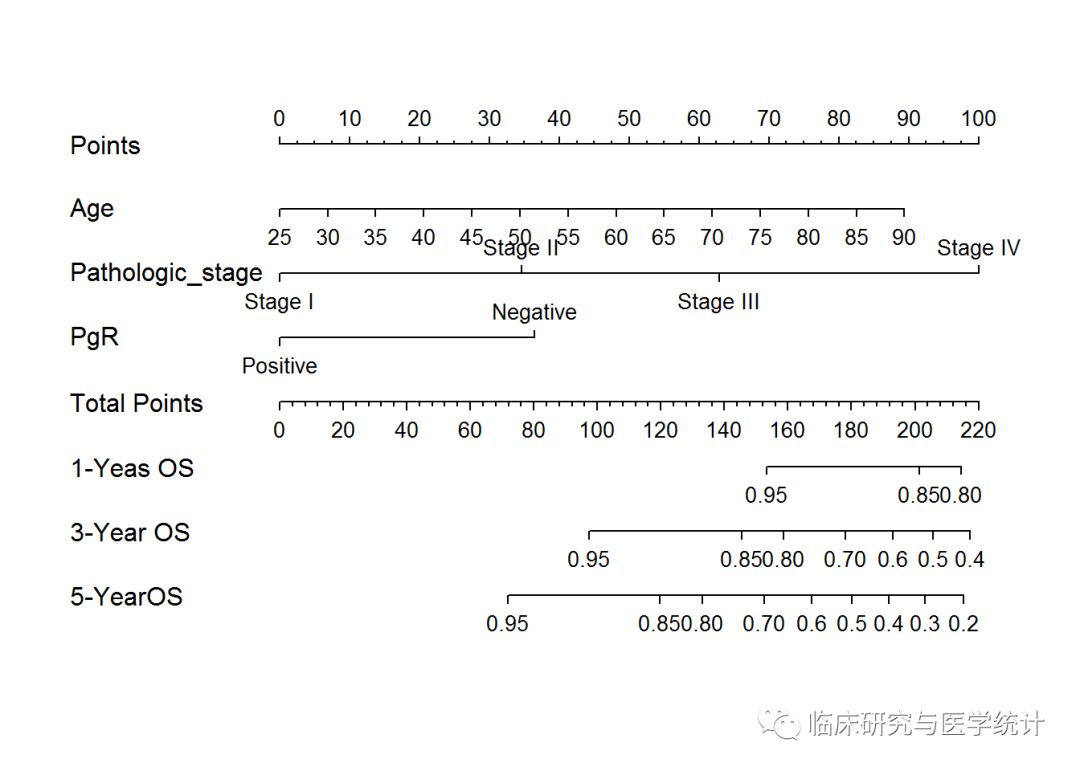
图1. 列线图。
结果解读:图中points就是一个选定的评分标准或者尺度,对于每个自变量取值,在该点做一条垂直于Points轴的直线(可通过直尺),交点即代表该自变量取值下的评分,如Age,取25时评分为0分,CEA为90时评分约为100分。以此类推,计算每个患者各个自变量对应的分值points,加起来就是总分totalpoints。同样的道理,在TotalPoints轴上找到该患者总分对应的点,画一垂直直接到生存概率轴上(如3年生存概率3-yearOS或者5年生存概率5-year OS),交点即为该患者的3年或5年生存概率。
计算C-index
- f<-coxph(Surv(Months,Status==1)~Age+Pathologic_stage+PgR,data=breast)
- sum.surv<-summary(f)
- c_index<-sum.surv$concordance
- c_index
- ## C se(C)
- ## 0.77878820 0.05734042
此处再次解释一下上述R语言代码中计算的C-Index统计量的含义,此值可以参考ROC曲线下面积去理解,取值范围0~1,越接近1说明我们构建的Cox回归模型预测价值越大,一般来说C-Index=0.7即表明模型具有良好的预测价值。本例中计算的C-Index = 0.7503, se(C-Index) = 0.02992,以上为软件直接输出结果。
计算C-index的补数(可选)
- library(Hmisc)
- S<-Surv(breast$Months,breast$Status==1)
- rcorrcens(S~predict(coxm),outx=TRUE)
- ##
- ## Somers' Rank Correlation for Censored Data Response variable:S
- ##
- ## C Dxy aDxy SD Z P n
- ## predict(coxm) 0.22 -0.559 0.559 0.09 6.21 0 549
构建标准曲线。u需要与之前f中定义好的time.inc一致,即f中time.inc为60时,此处u即为60;m要根据样本量来确定,由于标准曲线一般将所有样本分为3或4组(在图中显示3或4个点),m代表每组的样本量数,因此m*3应该等于或近似等于样本量。
- cal<- calibrate(coxm, cmethod='KM', method='boot', u=60, m=100, B=100)
- ## Using Cox survival estimates at 30 Days
- ## Warning in groupkm(cox, Surv(y[, 1], y[, 2]), u = u, cuts = orig.cuts): one
- ## interval had < 2 observations
打印并修改标准曲线的图形参数
- plot(cal,lwd=2,lty=1,errbar.col=c(rgb(0,118,192,maxColorValue=255)),xlim=c(0.7,1),ylim=c(0.6,1),xlab="Nomogram-Predicted Probability of 5-Year OS",ylab="Actual 5-Year OS(proportion)", col=c(rgb(192,98,83,maxColorValue=255)))
- lines(cal[,c("mean.predicted","KM")],type="b",lwd=2,col=c(rgb(192,98,83,maxColorValue=255)), pch=16)
- abline(0,1,lty=3,lwd=2,col=c(rgb(0,118,192,maxColorValue=255)))
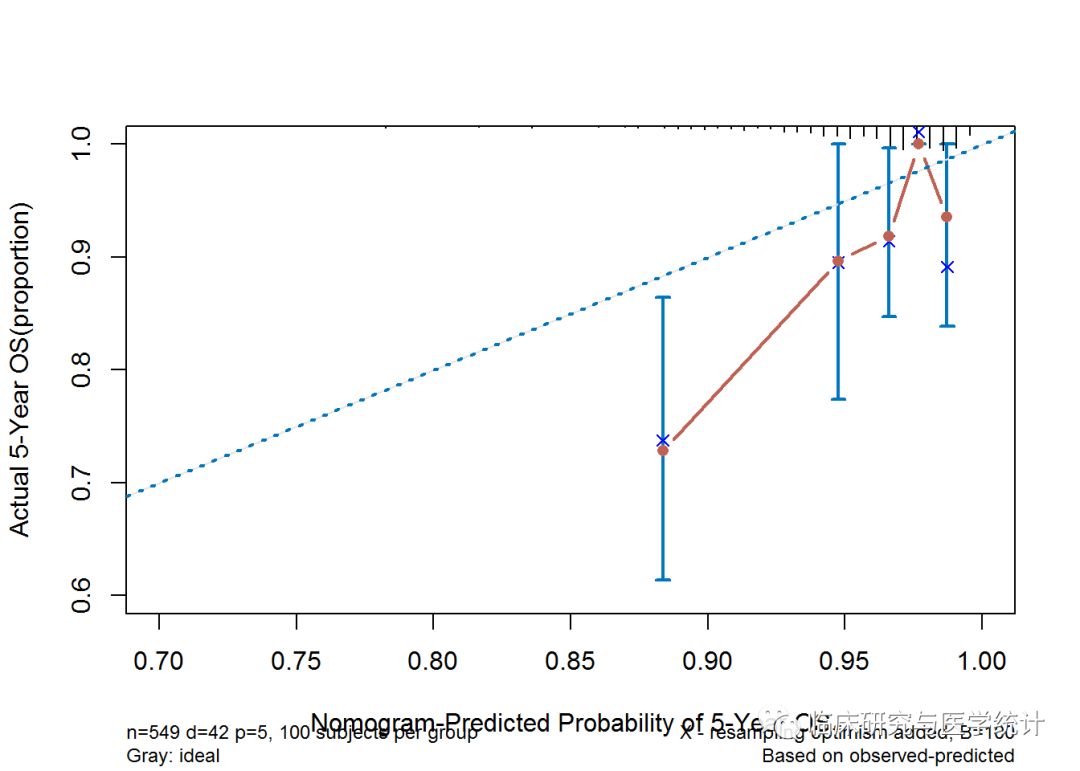
图2. 标准曲线。
基于训练集采用bootstrap冲抽样的方法验证列线图的预测准确性。结果解读:横坐标为根据列线图预测的每个患者的5年生存概率,纵坐标为每个患者实际的5年生存概率,如果图中的红色线条恰好与蓝色虚线完全重合时最为理想。
4. 总结与讨论
综上,本文介绍了生存资料预测模型的构建以及Nomogram的绘制。需要说明的是一个预测模型是否具有较好的实际运用价值,除了考量其预测的准确性还要考量其可操作性。除了内部验证检验其准确性,外部验证有时也是必须的,本例中因未获得较好的外部验证数据及并未演示外部验证的操作过程。过去十年有关临床预测模型的Nomogram文章很多,很多Nomogram的预测效能远高于TNM分期,可是为什么医生们仍然习惯运用TNM分期去为患者“算命”呢?我想主要原因还是TNM分期使用更为方便。从这个角度讲,我们构建Nomogram应该纳入尽可能少的变量以方便临床使用。到底应该优先考虑其准确性还是应该考虑其可操作性?读者应该根据自己的研究目的自行考量。
5. 参考文献
[1].周支瑞,胡志德.聪明统计学. 长沙:中南大学出版社, 2016.
[2].周支瑞,胡志德.疯狂统计学. 长沙:中南大学出版社, 2018.