1. 背景知识
前面的文章我们已经探讨了评价一个预测模型区分度的统计学指标C-statistics(即ROC曲线下面积)。但C-statistics是否足够好呢?没有最好,只有更好。比如我通过某个连续指标预测患者是否患病,无论选取哪个值作为截断值,都存在一定的假阳性和假阴性概率。既然这两种情况都无法避免,那我就从构建预测模型的原始动机出发,努力去寻找一个预测净受益最大的模型。如何去计算这种预测净收益呢?
纪念斯隆凯特琳癌症研究所的AndrewVickers等人于2006年发明了一种新的计算方法,叫决策曲线分析法(Decision Curve Analysis,DCA),与二战时期就诞生的ROC分析相比,DCA显然还很“嫩”,但“青出于蓝,而胜于蓝”,Ann Intern Med、JAMA、BMJ、J Clin Oncol等Top临床医学杂志都曾发文力挺使用决策曲线分析法(DCA)。那么问题来了?如何画出一副看起来足够高大上的Decision Curve?
统计学家们总是先想到用R去实现新的算法,事实也的确如此,基于R语言的DCA算法最先公布,后续也有基于SAS与Stata的DCA算法出现,但目前尚未见到SPSS具有此功能(SPSS的劣势在此也可见一斑)。Kerr等人还专门为决策曲线法的实现制作了一个名为DecisionCurve的R包,但请各位注意:目前DecisionCurve包在CRAN官网中已经不提供下载,原DecisionCurve包的所有函数已经整合入rmda包,所以大家只要在R中安装并加载rmda包即可绘制决策曲线。网上有关如何在新版本的R软件中安装DecisionCurve包的教程是一种不恰当的做法,正确做法是直接安装rmda包。
2. 案例分析
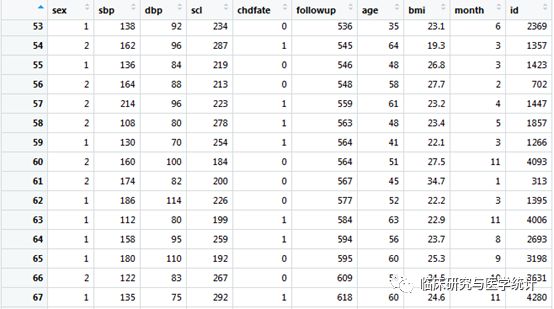
案例数据是NHLBI(美国国家心肺血液研究所)著名的Framingham心脏研究数据集的一个子集,包含4000多个样本。自变量分别为性别(sex)、收缩压(sbp)、舒张压(dbp)、血清胆固醇(scl)、年龄(age)、身体质量指数(bmi)等,因变量为冠心病相关死亡事件(chdfate)。因变量是二元变量,随访时间内死亡为1,未死亡为0。数据结构如下图1.所示:
图1. Framingham心脏研究数据集的子集截图
下面建立两个Logistic回归模型,来演示怎样画DCA曲线。一个是简单的Logistic回归模型(simple),以血清胆固醇值为预测变量(predictor),冠心病相关死亡事件为结果(outcome);另一个是多元Logistic回归模型(complex),以性别、年龄、BMI、血清胆固醇、收缩压、舒张压为预测变量,冠心病相关死亡事件为结果(outcome)。
3. R代码及结果解读
载入包 载入数据
- #install.packages("rmda")
- library(rmda)
- Data<-read.csv('2.20.Framingham.csv',sep = ',')
DCA模型构建
decision_curve()函数中,family=binomial(link=‘logit’)是使用logistic回归来拟合模型。threshold设置横坐标阈概率的范围,一般是01;但如果有某种具体情况,大家一致认为阈概率达到某个值以上,比如40%,则必须采取干预措施,那么0.4以后的研究就没什么意义了,可以设为00.4。by是指每隔多少距离计算一个数据点。Study.design可设置研究类型,是“cohort”还是“case-control”,当研究类型为“case-control”时,还应加上患病率population.prevalance参数,因为在“case-control”研究中无法计算患病率,需要事先提供。
首先构建一个简单模型,定义为simple
- simple<- decision_curve(chdfate~scl,data= Data,
- family = binomial(link ='logit'),
- thresholds= seq(0,1, by = 0.01),
- confidence.intervals = 0.95,
- study.design = 'case-control',
- population.prevalence = 0.3)
- ## Warning in decision_curve(chdfate ~ scl, data = Data, family =
- ## binomial(link = "logit"), : 33 observation(s) with missing data removed
- ## Calculating net benefit curves for case-control data. All calculations are done conditional on the outcome prevalence provided.
再构建一个复杂logistics回归模型complex,语法和simple相同,即在原来simple模型基础上增加自变量。
- complex<-decision_curve(chdfate~scl+sbp+dbp+age+bmi+sex,
- data = Data,family = binomial(link ='logit'),
- thresholds = seq(0,1, by = 0.01),
- confidence.intervals= 0.95,
- study.design = 'case-control',
- population.prevalence= 0.3)
- ## Warning in decision_curve(chdfate ~ scl + sbp + dbp + age + bmi + sex, data
- ## = Data, : 41 observation(s) with missing data removed
- ## Calculating net benefit curves for case-control data. All calculations are done conditional on the outcome prevalence provided.
- ## Note: The data provided is used to both fit a prediction model and to estimate the respective decision curve. This may cause bias in decision curve estimates leading to over-confidence in model performance.
把刚才计算的simple和complex两个对象合成一个list,并命名为List。
- List<- list(simple,complex)
DCA曲线绘制
plot_decision_curve() 函数的对象就是前面定义的List,如果只画一条曲线,直接把List替换成simple或complex即可。#curve.names是出图时,图例上每条曲线的名字,书写顺序要跟上面合成list时一致。cost.benefit.axis是另外附加的一条横坐标轴,损失收益比,默认值是TRUE,所在不需要时要记得设为FALSE。col设置颜色。confidence.intervals设置是否画出曲线的置信区间,standardize设置是否对净受益率(NB)使用患病率进行校正。可得如图2.所示曲线。
- plot_decision_curve(List,
- curve.names=c('simple','complex'),
- cost.benefit.axis =FALSE,col= c('red','blue'),
- confidence.intervals=FALSE,
- standardize = FALSE)
- ## Note: When multiple decision curves are plotted, decision curves for 'All' are calculated using the prevalence from the first DecisionCurve object in the list provided.
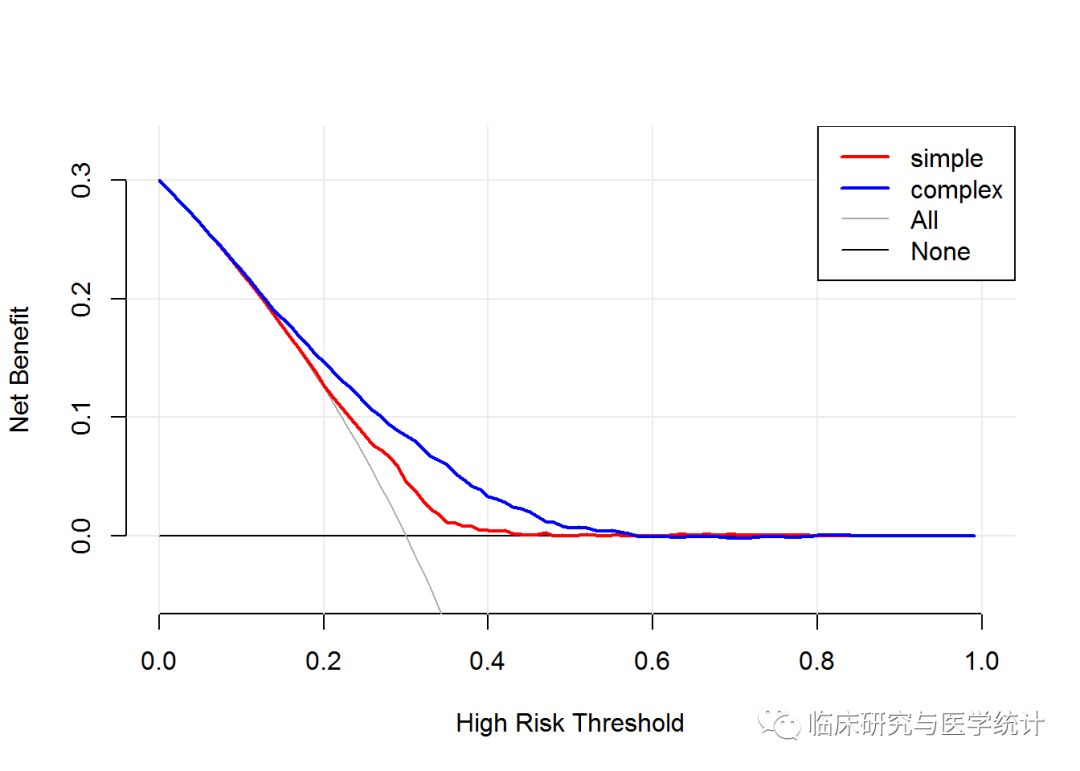
图2. 决策曲线。
可见,在阈值在0.1~0.5大致范围内,complex模型的净受益率都比simple模型高。
查看complex模型曲线上的各数据点,NB也可以改成sNB,表示经过患病率的标准化。
- summary(complex,measure= 'NB')
- 此结果太冗长,故不在此展示,读者可以自行在R语言中尝试。
绘制临床影响曲线(Clinical Impact Curve)
绘制simple模型的临床影响曲线。使用simple模型预测1000人的风险分层,显示“损失:受益”坐标轴,赋以8个刻度,显示置信区间,得到图3
- plot_clinical_impact(simple,population.size= 1000,
- cost.benefit.axis = T,
- n.cost.benefits= 8,
- col =c('red','blue'),
- confidence.intervals= T,
- ylim=c(0,1000),
- legend.position="topright")
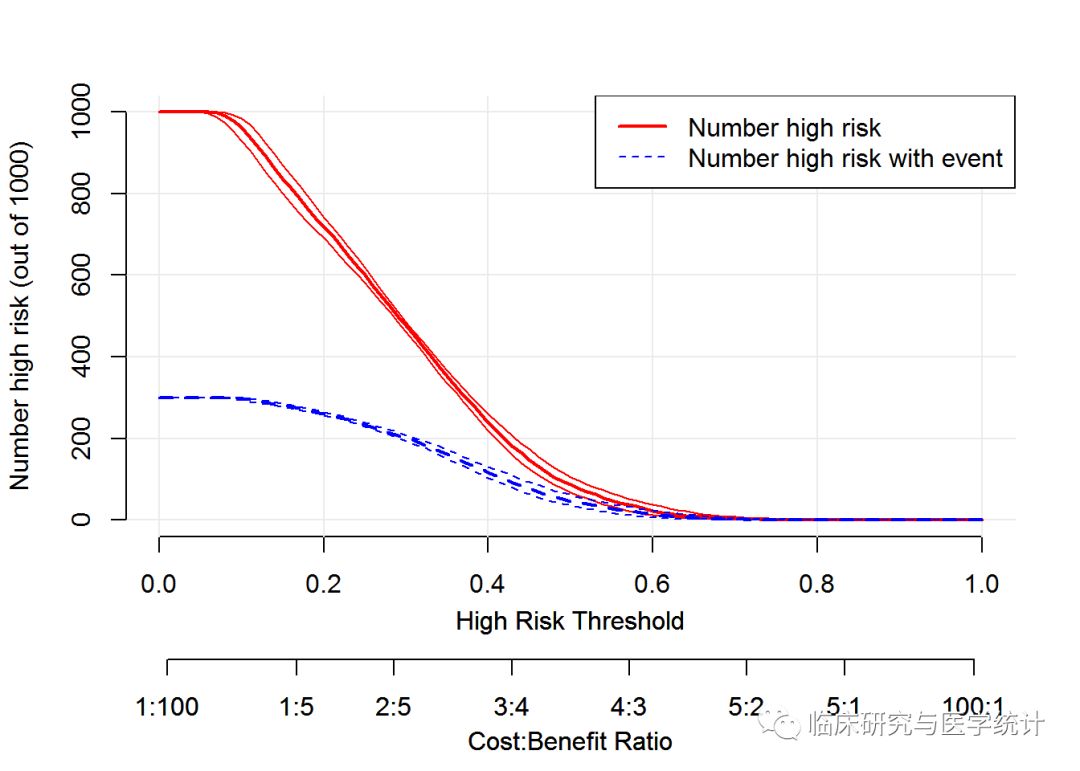
图3. simple模型临床影响曲线
绘制complex模型的临床影响曲线。使用complex模型预测1000人的风险分层,显示“损失:受益”坐标轴,赋以8个刻度,显示置信区间,得到图4.
- plot_clinical_impact(complex,population.size= 1000,
- cost.benefit.axis = T,
- n.cost.benefits= 8,col =c('red','blue'),
- confidence.intervals=T,
- ylim=c(0,1000),
- legend.position="topright")
图4. complex模型临床影响曲线
红色曲线(Number high risk)表示,在各个阈概率下,被simple模型(图3.)或complex模型(图4.)划分为阳性(高风险)的人数;蓝色曲线(Number high risk with outcome)为各个阈概率下真阳性的人数。
4. 参考文献
[1]. Decision curve analysis: anovel methodfor evaluating prediction models
[2].Decision curve analysisrevisited:overall net benefit, relationships to ROC curve analysis, andapplication tocase-control studies
[3].Assessing the Clinical Impactof RiskPrediction Models With Decision Curves: Guidance for CorrectInterpretation andAppropriate Use
[4]. https://www.plob.org/article/12455.html 决策曲线分析法(Decision Curve Analysis, DCA)
[5].https://www.mskcc.org/departments/epidemiology-biostatistics/health-outcomes/decision-curve-analysis-01
[6]. https://github.com/mdbrown/rmda/releases