生存分析中连续型自变量截断值的确定方法

题记：本文重点讲解在生存分析中如何合理设置连续型自变量的截断值，将连续型自变量转换为二分类变量。

1. 背景知识

对于结果变量为二分类资料的数据，连续型自变量截断值的确定一般通过ROC分析，我们通常选用约登指数（敏感度+特异度-1）最大的点为最佳截断值（cut-off值)点，这些都是常用的统计学方法，可以参考笔者与胡志德博士主编《聪明统计学》的相关章节[1]。但有时我们面对的问题要更复杂，假定我们的结果已经不是单纯的二分类资料，而是包含有时间因素的分类资料（Time to event data），即我们常说的生存资料。

举个简单例子，假定在某研究中我们定义生存资料的结局是死亡，那作为研究者来说不仅关心研究对象是否死亡，而且关心研究对象从入组开始到死亡的时间长度。比如某研究中试验组共入组100人，假定在入组后的第1年、第2年、第3年死亡人数分别为：0、0、90人；对照组同样入组100人，假定入组后第1年、第二年、第3年死亡人数分别为：90、0、0。在这样一个例子中，如果我们只看重死亡的人数，那么试验组与对照组结果没有差别，如果我们同时关注死亡与发生死亡的时间，那显然试验组的结局要优于对照组。从结局变量的维度上讲，生存资料在二分类的资料的基础上又增加了时间的维度。

那么对于生存资料中的连续型自变量是否还可以直接采用常规ROC分析来确定截断值呢？在既往已经发表的文献中我们有时会看到有些作者确实直接采用常规ROC分析方法确定生存资料中连续型自变量的截断值，那么这样的做法是否妥当？笔者认为，这种做法目前不好判断正确与否，但至少是不妥当的，因为我们有更科学的方法。本文中，我们将介绍三种方法来处理此类问题。本文的数据来自于笔者自己的研究中使用到的数据，数据下载自TheCancer Genome Atlas（TCGA）数据库，为了方便读者阅读，我们也对数据进行了简化处理，让其看起来更具有代表性，方便大家根据自己的研究数据进行实践操作。

2. 案例分析

【案例1】笔者在TheCancer Genome Atlas（TCGA）数据中下载了1215例乳腺癌患者的临床资料与相对基因表达信息。下载网址：https://genome-cancer.ucsc.edu/，数据版本：2015-02-24；DatasetID：TCGA_BRCA_exp_HiSeqV2。临床数据与基因表达信息按照芯片编号进行严格匹配后，我们从中提取了这1215例患者的生存时间，结局状态、X基因的相对表达水平。我们的研究目的是把X基因通过合适的截断值二分为X基因低表达和X基因高表达组，然后通过生存分析判断这两个组的预后是否有差异。本例中生存时间单位：天，NA表示数据缺失；我们定义的结局为死亡，1：死亡，0：截尾；X基因表达水平为经过标准化之后的基因含量，是连续型数据。读者朋友请注意：此处X基因可以替换为与预后可能有关的任何连续型自变量，比如任何分子标志物含量、实验室检查指标的数值、年龄、体重、血压等等。数据整理如下表1所示。

表1.1215例患者X基因表达水平与生存资料

2.1 中位数法确定截断值

通过中位数确定截断值是最为常用的一种截断值确定的方法，类似的还有通过均值确定截断值，通过四分位数间距确定截断值等。这些方法可归为一类，这种方法操作简单，而且容易被读者理解和接受。下面我们就通过IBMSPSS 22.0（IBMSPSS, NY, USA）软件演示下中位数确定截断值，如图1~图7所示。

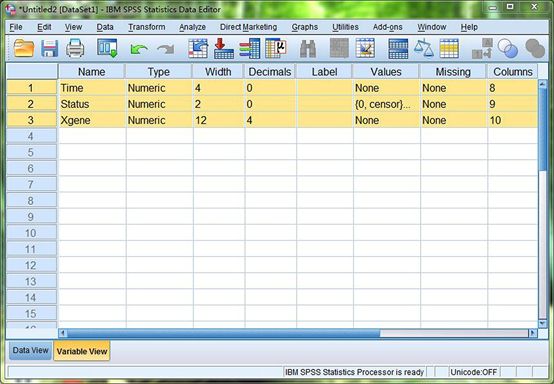
图1. 定义变量Time: 生存时间；Status: 生存结局；Xgene:X基因的表达水平

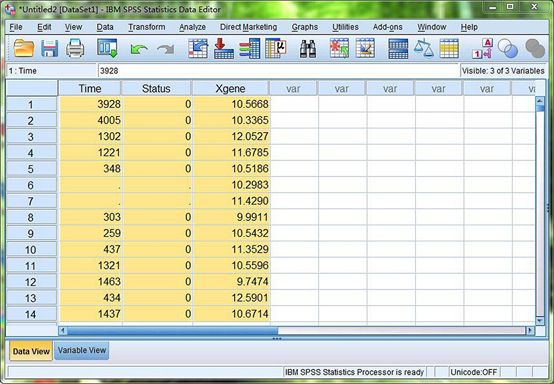
图2. 录入数据

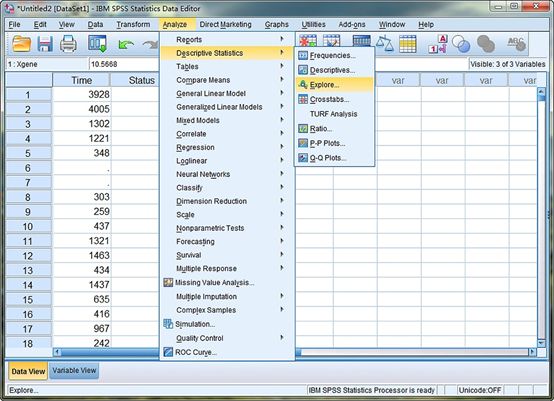
图3. 计算Xgene的中位数，依次选择“Analyze”-“Descriptive Statistics”-“Explore”。

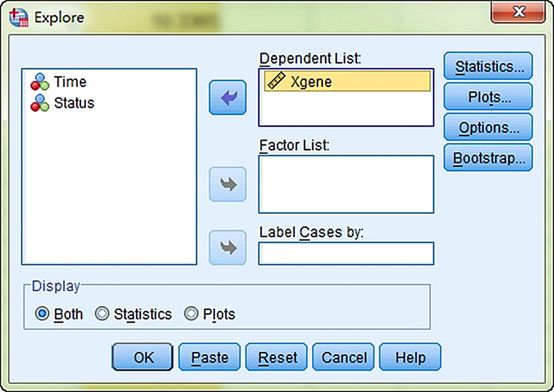
图4. 计算Xgene的中位数，选择“Xgene”进入“Dependent List”，其他选项默认，点击“OK”。

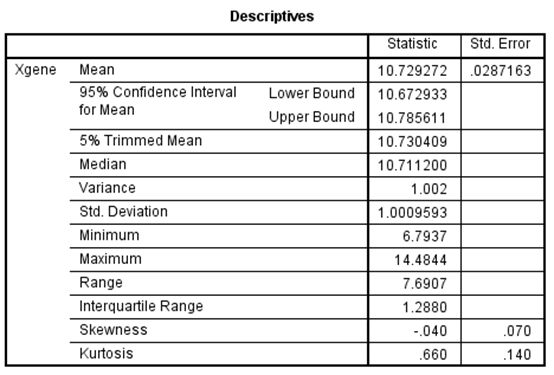
图5. 计算结果。Xgene的中位数=10.7112，为了方便阅读，我们取值10.71。

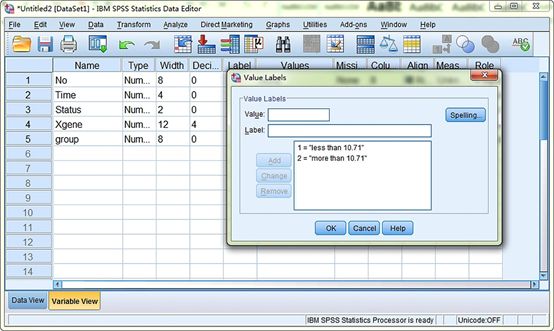
图6. 新建分组变量“group”：小于10.71为基因低表达组，不小于10.71为高表达组。

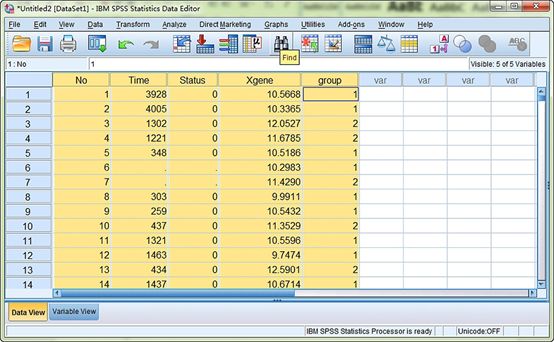
图7. 重新整理数据：录入每个患者具体分组信息。后续按照分组变量进行生存分析等。注意：此处使用Excel软件进行分组操作更方便，按照Xgene表达相对水平从低到高排序，找到中位数10.71，小于10.71分组为1，大于10.71分组为2。

2.2 X-tile软件法确定截断值

上述通过中位数的方法确定截断值优点是操作简便、读者易接受，但通过中位数这类简单的方法确定的截断值是否为最佳截断值呢？笔者认为，如果研究者足够幸运也许中位数就是最佳的截断值，这种简单的方法多少带有一些“运气”的成分。那我们接下来介绍一种更为科学的生存资料中连续型自变量最佳截断值的确定方法：通过X-tile软件确定生存资料中连续型自变量的最佳截断值。该软件支持对连续型自变量进行二分类和三分类，其背后的统计学原理在此我们不做详细介绍，感兴趣的读者可以阅读文末参考文献的全文。如果我们在论文写作过程中使用了X-Tile这个软件确定截断值，引用这篇参考文献即可[2]。X-tile软件下载地址：http://medicine.yale.edu/lab/rimm/research/software.aspx。下面我们就演示其操作过程，我们继续采用【案例1】的数据，如图8~图13所示。

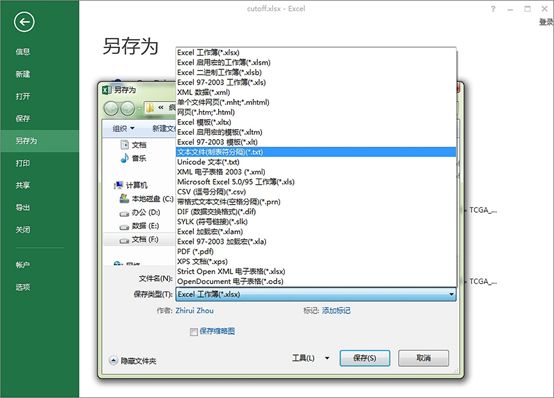
图8. 数据准备。将数据存储为文本文件（制表符分隔）。X-tile软件要求此格式数据。

图9. 启动X-tile软件，点击“Analyze”。

图10. 导入数据文件。依次点击“File”-“Open”，选择要打开的数据。

图11. 选择文本文件（制表符分隔）格式的数据打开。

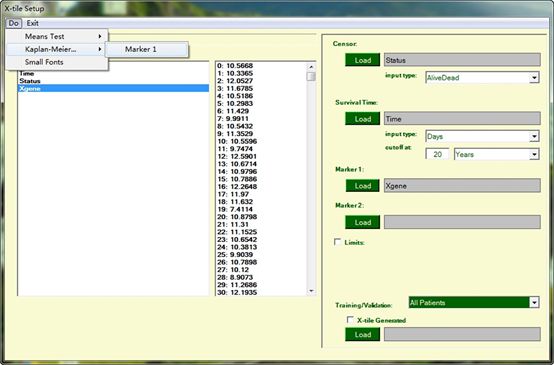
图12. 如图设置参数。依次设置：Censor选入“Status”变量，SurvivalTime选入“Time”变量，单位选择“Days”，Marker1选入“Xgene”变量。然后依次点击“Do”-“Kaplan-Meier”-“Marker1”。

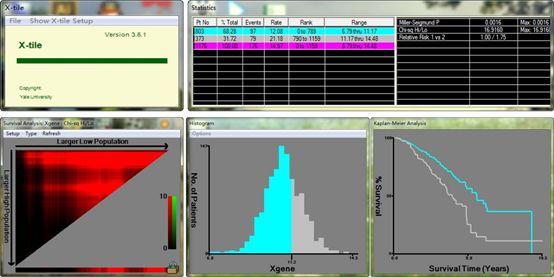
图13. 将光标移至上图左下方X轴上红色区域单击，即可得计算结果，本例中最佳截断值为11.17，按照此截断值划分后的Kaplan-Meier曲线如上图右下方所示。此处需要注意的是，如果把光标移至上图左下方三角形红色与黑色相间区域，则可对此连续型变量三分，读者可自行尝试。确定截断值后的后续数据分组与整理数据操作与2.1相同，此处不再赘述。

2.3 SurvivalROC法确定截断值

以上通过X-Tile软件确定截断值的方法操作简便，结果可靠，输出的结果也较丰富。有些读者除了需要获得生存资料中连续型自变量的最佳截断值点，可能还需要像普通ROC分析一样画出ROC曲线并计算出曲线下的面积，这时我们也可以通过R软件（version 3.3.3）的survivalROC程序包进行计算（version 1.0.3）[3-4]。我们继续使用【案例1】的数据，R软件操作代码如下：

library(survivalROC)#载入程序包

data<-read.csv(file.choose())#导入外部数据，首先把整理后的数据另存为.csv格式

nobs<- NROW(data) #定义数据集的行数

cutoff<- 3650 #设定为10年生存时间，读者可根据需求设定为3年、5年等。

#Delete "NA"

data<-data[which(data$Status!="NA"),]

#将结果变量中缺失数据删除，读者根据自己数据特点决定是否需要此命令。

#Fit survival ROC model with method of "KM"

SROC= survivalROC(Stime = data$Time, 

                     Status = data$Status,     

                     marker = data$Xgene,    

                     predict.time = cutoff, method= "KM" ) #构建生存函数

cut.op= SROC$cut.values[which.max(SROC$TP-SROC$FP)] #计算最佳截断值

cut.op#输出最佳截断值

#plot survival ROC #绘制survival ROC曲线，并设置图形参数。

plot(SROC$FP,SROC$TP, type="l", xlim=c(0,1), ylim=c(0,1),  

     xlab = paste( "FP","\n", "AUC = ",round(SROC$AUC,3)),

     ylab = "TP",main = "10-yearsurvival ROC", col="red")

abline(0,1)

legend("bottomright",c("Xgene expression"),col="red",lty=c(1,1))

按照10年生存时间，最后计算的截断值为11.0686，后续可以按照前述方法整理数据进行生存分析等。同时我们也使用R软件画出了survivalROC曲线，计算了曲线下面积（AUC），如图14所示。

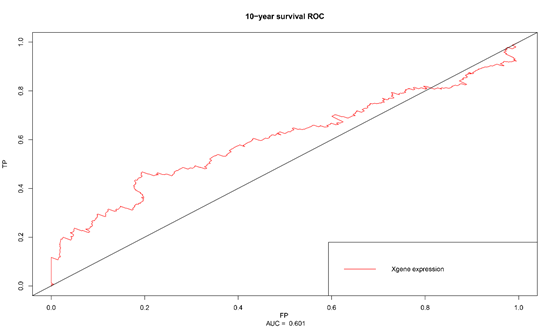
图14. survivalROC曲线，AUC=0.601。

3. 总结与讨论

综上，笔者总结了在生存资料中连续型自变量截断值确定的三种方法，笔者推荐第二种截断值确定的方法，该方法性价比较高，结果直观，对于临床医生来说易学易用。第一种方法较为简单，但很难确定中位数是否为最佳截断值。第三种方法也是一种较好的方法，但需要有一定R语言的基础，对于临床医生来说可能有一定的难度。细心的读者可能发现第二种方法与第三种方法计算的结果并不相同，事实上这两种方法背后的统计学原理是不同的，计算结果存在差异并不奇怪。即便是第三种方法，我们设定不同的时间节点，比如把本例中的10-year survivalROC更换为5-yearsurvivalROC（调整predict.time= cutoff设置），计算的截断值也不同，读者可以自行尝试。但以上三种方法在论文中使用都是可行的。论文写作时我们也可以同时采用以上三种方法确定截断值，如果三种方法可以得到类似的结论，那说明结论比较稳健。

4. 参考文献

[1]. 周支瑞,胡志德.聪明统计学. 长沙:中南大学出版社, 2016.

[2]. Camp R L, Dolled-Filhart M, Rimm D L. X-tile:a new bio-informatics tool for biomarker assessment and outcome-based cut-pointoptimization [J]. Clin Cancer Res, 2004, 10(21): 7252-9.

[3]. Heagerty, P.J., Lumley, T., Pepe, M. S. (2000) Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker Biometrics, 56, 337-344.

[4]. 周支瑞,胡志德.疯狂统计学. 长沙:中南大学出版社, 2018.