题记:我们在以前的文章中介绍了竞争风险模型的R语言实现,今天我们与各位朋友分享如何基于竞争风险模型绘制列线图,以飨读者。
1. 背景知识
在观察某事件是否发生时,如果该事件被其他事件阻碍,即存在所谓“竞争风险”。研究中结局事件可能有多个,某些结局将阻止感兴趣事件的出现或影响其发生的概率,各结局事件形成“竞争”关系,互为竞争风险事件。
举例来说,某研究人员收集了本市2007年确诊为轻度认知损害(MCI)的518例老年患者临床资料,包括基本人口学特征、生活方式、体格检查和合并疾病信息等,并于2010~2013年完成6次随访调查,主要观察结局为发生阿尔兹海默病(AD)。随访期间,共发生AD78例,失访84例,其中28例搬迁、31例退出、25例死亡。试问影响MCI向AD转归的因素都有哪些?本例中,如果MCI患者在观察期间死于癌症、心血管疾病、车祸等原因而未发生AD,就不能为AD的发病做出贡献,即死亡“竞争”了AD的发生。传统生存资料统计方法将发生AD前死亡的个体、失访个体和未发生AD个体均按删失数据(censored data)处理,可能会导致估计偏差[1]。对于死亡率较高的老年人群,当有竞争风险事件存在时,采用传统生存分析方法(K-M法、Cox比例风险回归模型)会高估所研究疾病的发生风险,产生竞争风险偏倚,有人专门研究发现约46%的文献可能存在这种偏倚。
本例中若选用竞争风险模型处理较为恰当。所谓竞争风险模型(Competing Risk Model)是一种处理多种潜在结局生存数据的分析方法,早在1999年Fine和Gray就提出了部分分布的半参数比例风险模型,通常使用的终点指标是累积发生率函数(Cumulative incidence function,CIF)[1-2]。本例中可以将发生AD前死亡作为AD的竞争风险事件,采用竞争风险模型进行统计分析。竞争风险的单因素分析常用来估计关心终点事件的发生率,多因素分析常用来探索预后影响因素及效应值。
2. 案例分析
2.1 [案例分析]
本案例数据来自http://www.stat.unipg.it/luca/R/。有研究者探讨骨髓移植对比血液移植治疗白血病的疗效,结局事件定义为“复发”,某些患者移植后不幸因为移植不良反应死亡,那这些发生移植相关死亡的患者就无法观察到“复发”的终点,也就是说“移植相关死亡”与“复发”存在竞争风险。故采用竞争风险模型分析[3-4]。
首先从当前工作路径中导入数据文件’bmtcrr.csv’。
- library(foreign)
- bmt <-read.csv('bmtcrr.csv')
- str(bmt)
- ## 'data.frame': 177 obs. of 7 variables:
- ## $ Sex : Factor w/ 2 levels "F","M": 2 1 2 1 1 2 2 1 2 1 ...
- ## $ D : Factor w/ 2 levels "ALL","AML": 1 2 1 1 1 1 1 1 1 1 ...
- ## $ Phase : Factor w/ 4 levels "CR1","CR2","CR3",..: 4 2 3 2 2 4 1 1 1 4 ...
- ## $ Age : int 48 23 7 26 36 17 7 17 26 8 ...
- ## $ Status: int 2 1 0 2 2 2 0 2 0 1 ...
- ## $ Source: Factor w/ 2 levels "BM+PB","PB": 1 1 1 1 1 1 1 1 1 1 ...
- ## $ ftime : num 0.67 9.5 131.77 24.03 1.47 ...
这是一个数据框结构的数据,含有7个变量,共177个观测。
$ Sex : 因子变量,2个水平:“F”,“M”。
$ D : 因子变量,2个水平:“ALL(急性淋巴细胞白血病)”,“AML(急性髓系细胞白血病)”。
$ Phase : 因子变量,4个水平:“CR1”,“CR2”,“CR3”,“Relapse”。
$ Age : 年龄。
$ Status: 结局,0=删失,1=复发,2=竞争风险事件。
$ Source: 因子变量,2个水平:“BM+PB(骨髓移植+血液移植)”,“PB(血液移植)”。
$ ftime : 时间。
在R中加载竞争风险模型的程辑包cmprsk,使用cuminc()函数及crr()函数即可进行考虑竞争风险事件生存资料的单因素分析与多因素分析,我们在前文已经详细述及基于R语言实现的方式,此处不表。
如何对竞争风险模型进行可视化?如何绘制列线图?
下面我们基于R演示如何绘制竞争风险模型的列线图。
首先,对数据集bmt中的变量进行进一步处理。
- bmt$id<-1:nrow(bmt)#将数据集按照行排序并生成序号id
- bmt$age <- bmt$Age
- bmt$sex <- as.factor(ifelse(bmt$Sex=='F',1,0))
- bmt$D <- as.factor(ifelse(bmt$D=='AML',1,0))
- bmt$phase_cr <- as.factor(ifelse(bmt$Phase=='Relapse',1,0))
- bmt$source = as.factor(ifelse(bmt$Source=='PB',1,0))
查看数据结构,并展示前6行。我们对数据集中的协变量重新进行了赋值,并对多分类变量进行了二值化。注意,此处多分类变量我们并未设置哑变量,主要考量是:在列线图中如果出现哑变量的情形,结果解读会让人困惑,所以列线图中应避免哑变量的情形,可考虑根据专业知识将多分类变量按照等级资料处理或者二值化。
- str(bmt)
- ## 'data.frame': 177 obs. of 12 variables:
- ## $ Sex : Factor w/ 2 levels "F","M": 2 1 2 1 1 2 2 1 2 1 ...
- ## $ D : Factor w/ 2 levels "0","1": 1 2 1 1 1 1 1 1 1 1 ...
- ## $ Phase : Factor w/ 4 levels "CR1","CR2","CR3",..: 4 2 3 2 2 4 1 1 1 4 ...
- ## $ Age : int 48 23 7 26 36 17 7 17 26 8 ...
- ## $ Status : int 2 1 0 2 2 2 0 2 0 1 ...
- ## $ Source : Factor w/ 2 levels "BM+PB","PB": 1 1 1 1 1 1 1 1 1 1 ...
- ## $ ftime : num 0.67 9.5 131.77 24.03 1.47 ...
- ## $ id : int 1 2 3 4 5 6 7 8 9 10 ...
- ## $ age : int 48 23 7 26 36 17 7 17 26 8 ...
- ## $ sex : Factor w/ 2 levels "0","1": 1 2 1 2 2 1 1 2 1 2 ...
- ## $ phase_cr: Factor w/ 2 levels "0","1": 2 1 1 1 1 2 1 1 1 2 ...
- ## $ source : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1 1 1 ...
- head(bmt)
- ## Sex D Phase Age Status Source ftime id age sex phase_cr source
- ## 1 M 0 Relapse 48 2 BM+PB 0.67 1 48 0 1 0
- ## 2 F 1 CR2 23 1 BM+PB 9.50 2 23 1 0 0
- ## 3 M 0 CR3 7 0 BM+PB 131.77 3 7 0 0 0
- ## 4 F 0 CR2 26 2 BM+PB 24.03 4 26 1 0 0
- ## 5 F 0 CR2 36 2 BM+PB 1.47 5 36 1 0 0
- ## 6 M 0 Relapse 17 2 BM+PB 2.23 6 17 0 1 0
regplot包中的regplot()函数可绘制较为美观的nomogram。但是,它目前只接收coxph()、lm()和glm()函数返回的回归对象。因此,为了绘制竞争风险模型的nomogram,我们需要对原数据集加权创建一个新数据集用于为竞争风险模型分析[5-6]。mstate包中的crprep()函数的功能主要在于创建此加权数据集,如下面的R代码所示。然后,我们就可以使用coxph()函数对加权数据集进行竞争风险模型拟合,然后传递给regplot()来绘制nomogram。具体加权原理读者可参考Geskus RB等人发表的文献[5],此处不表。
下面,我们对原数据集bmt创建加权数据集并命名为df.w。其中,参数trans=指定需要加权计算的终点事件与竞争风险事件;cens=指定截尾;id=传入数据集bmt的id;keep=数据集中需要保留的协变量。
- library(mstate)
- ## Loading required package: survival
- df.w <- crprep("ftime", "Status",
- data=bmt, trans=c(1,2),
- cens=0, id="id",
- keep=c("age","sex","D","phase_cr","source"))
- df.w$T<- df.w$Tstop - df.w$Tstart
上述代码已经创建一个加权数据集df.w,然后我们可以在此数据集上使用coxph()函数进行竞争风险分析。
- m.crr<- coxph(Surv(T,status==1)~age+sex+D+phase_cr+source,
- data=df.w,
- weight=weight.cens,
- subset=failcode==1)
- summary(m.crr)
- ## Call:
- ## coxph(formula = Surv(T, status == 1) ~ age + sex + D + phase_cr +
- ## source, data = df.w, weights = weight.cens, subset = failcode ==
- ## 1)
- ##
- ## n= 686, number of events= 56
- ##
- ## coef exp(coef) se(coef) z Pr(>|z|)
- ## age -0.02174 0.97850 0.01172 -1.854 0.06376 .
- ## sex1 -0.10551 0.89987 0.27981 -0.377 0.70612
- ## D1 -0.53163 0.58764 0.29917 -1.777 0.07556 .
- ## phase_cr1 1.06140 2.89040 0.27870 3.808 0.00014 ***
- ## source1 1.06564 2.90269 0.53453 1.994 0.04620 *
- ## ---
- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
- ##
- ## exp(coef) exp(-coef) lower .95 upper .95
- ## age 0.9785 1.0220 0.9563 1.001
- ## sex1 0.8999 1.1113 0.5200 1.557
- ## D1 0.5876 1.7017 0.3269 1.056
- ## phase_cr1 2.8904 0.3460 1.6739 4.991
- ## source1 2.9027 0.3445 1.0181 8.275
- ##
- ## Concordance= 0.737 (se = 0.037 )
- ## Likelihood ratio test= 28.33 on 5 df, p=3e-05
- ## Wald test = 28.54 on 5 df, p=3e-05
- ## Score (logrank) test = 30.49 on 5 df, p=1e-05
接下来,我们可以使用regplot()函数绘制nomogram。在nomogram中,将数据集中id=31的患者各协变量的取值映射到相应的得分,并计算总得分,并分别计算其在36个月和60个月的累计复发概率,此概率即为控制了竞争风险的累计复发概率,分别为:0.196和0.213。
- library(regplot)
- regplot(m.crr,observation=df.w[df.w$id==31&df.w$failcode==1,],
- failtime = c(36, 60), prfail = T, droplines=T)
- ## Replicate weights assumed
- ## Click on graphic expected. To quit click Esc or press Esc
- # $points.tables
- ## $points.tables[[1]]
- ## source Points
- ## source2 1 100
- ## source1 0 38
- ##
- ## $points.tables[[2]]
- ## phase_cr Points
- ## phase_cr1 0 38
- ## phase_cr2 1 100
- ##
- ## $points.tables[[3]]
- ## D Points
- ## D2 1 8
- ## D1 0 38
- ##
- ## $points.tables[[4]]
- ## sex Points
- ## sex1 0 38
- ## sex2 1 32
- ##
- ## $points.tables[[5]]
- ## age Points
- ## 1 0 78
- ## 2 10 65
- ## 3 20 53
- ## 4 30 40
- ## 5 40 28
- ## 6 50 15
- ## 7 60 3
- ## 8 70 -10
- ##
- ## $points.tables[[6]]
- ## Total Points Pr( T < 36 )
- ## 1 100 0.0232
- ## 2 150 0.0543
- ## 3 200 0.1243
- ## 4 250 0.2705
- ## 5 300 0.5276
- ## 6 350 0.8318
- ## 7 400 0.9856
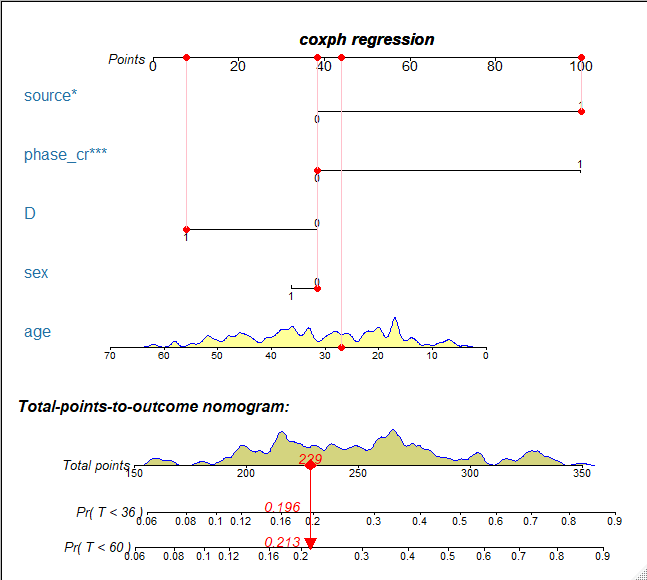
图 1. 使用竞争风险模型预测36月和60月累积复发风险的Nomogram。根据nomogram的估计,31号患者在36月和60月累积复发风险概率分别为0.196和0.213。
为了便于比较,我们可进一步在原数据集bmt中构建Cox回归模型,同样计算id=31的患者各协变量的取值映射到相应的得分,并计算总得分,并计算其在36个月和60个月的累计复发概率,计算结果分别为:0.205和0.217。
- library(survival)
- m.cph<-coxph(Surv(ftime,Status==1)~age+sex+D+phase_cr+source,
- data=bmt)
- summary(m.cph)
- ## Call:
- ## coxph(formula = Surv(ftime, Status == 1) ~ age + sex + D + phase_cr +
- ## source, data = bmt)
- ##
- ## n= 177, number of events= 56
- ##
- ## coef exp(coef) se(coef) z Pr(>|z|)
- ## age -0.007766 0.992264 0.011952 -0.650 0.5158
- ## sex1 0.371888 1.450470 0.283306 1.313 0.1893
- ## D1 -0.643592 0.525402 0.295888 -2.175 0.0296 *
- ## phase_cr1 1.373882 3.950657 0.290598 4.728 2.27e-06 ***
- ## source1 0.315122 1.370427 0.552842 0.570 0.5687
- ## ---
- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
- ##
- ## exp(coef) exp(-coef) lower .95 upper .95
- ## age 0.9923 1.0078 0.9693 1.0158
- ## sex1 1.4505 0.6894 0.8324 2.5273
- ## D1 0.5254 1.9033 0.2942 0.9383
- ## phase_cr1 3.9507 0.2531 2.2352 6.9828
- ## source1 1.3704 0.7297 0.4637 4.0498
- ##
- ## Concordance= 0.726 (se = 0.036 )
- ## Likelihood ratio test= 30.74 on 5 df, p=1e-05
- ## Wald test = 29.99 on 5 df, p=1e-05
- ## Score (logrank) test = 33.48 on 5 df, p=3e-06
- regplot(m.cph,observation=bmt[bmt$id==31,],
- failtime = c(36,60), prfail = TRUE,droplines=T)
- ## Click on graphic expected. To quit click Esc or press Esc
- # $points.tables
- ## $points.tables[[1]]
- ## source Points
- ## source2 1 48
- ## source1 0 32
- ##
- ## $points.tables[[2]]
- ## phase_cr Points
- ## phase_cr1 0 32
- ## phase_cr2 1 100
- ##
- ## $points.tables[[3]]
- ## D Points
- ## D2 1 0
- ## D1 0 32
- ##
- ## $points.tables[[4]]
- ## sex Points
- ## sex1 0 32
- ## sex2 1 50
- ##
- ## $points.tables[[5]]
- ## age Points
- ## 1 0 44
- ## 2 20 36
- ## 3 40 28
- ## 4 60 21
- ## 5 80 13
- ##
- ## $points.tables[[6]]
- ## Total Points Pr( ftime < 36 )
- ## 1 100 0.0894
- ## 2 120 0.1308
- ## 3 140 0.1892
- ## 4 160 0.2695
- ## 5 180 0.3751
- ## 6 200 0.5053
- ## 7 220 0.6514
- ## 8 240 0.7935
- ## 9 260 0.9057
- ## 10 280 0.9708
- ## 11 300 0.9950
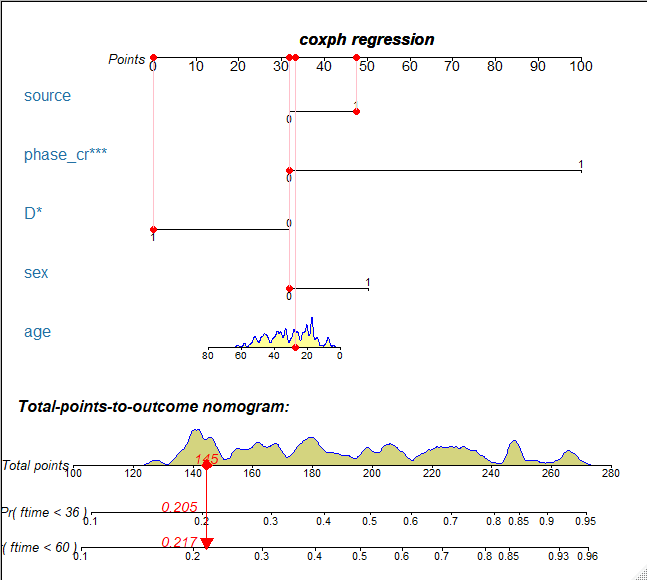
图 2. 使用Cox比例风险模型预测36月和60月累积复发风险的Nomogram。根据Nomogram估计,31号患者在36月和60月累积复发风险概率分别为0.205和0.217。
可见,基于竞争风险模型与Cox比例风险模型计算累计复发风险略有差异,竞争风险模型计算的31号患者累计复发风险略小。31号患者发生了我们定义的终点事件,即该患者为在移植后复发,根据竞争风险与Cox比例风险模型计算所得结果差别较小,当某患者截尾或者发生竞争风险事件,两个模型结算结果差别较大,读者可自行尝试。
3. 讨论和总结
本文详细介绍了使用R的mstate与regplot程辑包进行竞争风险模型列线图绘制。这其实是一种变通的方法,即首先对原数据集进行加权处理,然后使用Cox回归模型基于加权数据集构建竞争风险模型,然后绘制列线图。本文并未介绍对竞争风险模型进行进一步评价,R中riskRegression包可以对基于竞争风险模型构建的预测模型进行进一步评价,比如计算C-index,绘制校准曲线等。
4. 参考文献
[1]. Fine JP and Gray RJ (1999) A proportional hazards model for the subdistribution of a competing risk. JASA 94:496-509.
[2]. Gray RJ (1988) A class of K-sample tests for comparing the cumulative incidence of a competing risk, ANNALS OF STATISTICS, 16:1141-1154.
[3]. Scrucca L., Santucci A., Aversa F. (2007) Competing risks analysis using R: an easy guide for clinicians. Bone Marrow Transplantation, 40, 381-387.
[4]. Scrucca L., Santucci A., Aversa F. (2010) Regression modeling of competing risk using R: an in depth guide for clinicians. Bone Marrow Transplantation, 45, 1388–1395.
[5]. Geskus RB. Cause-specific cumulative incidence estimation and the fine and gray model under both left truncation and right censoring. Biometrics 2011;67:39-49.
[6]. Zhang Z, Cortese G, Combescure C, Marshall R, Lee M, Lim HJ, Haller B; written on behalf of AME Big-Data Clinical Trial Collaborative Group. Overview of model validation for survival regression model with competing risks using melanoma study data. Ann Transl Med 2018;6(16):325. doi: 10.21037/atm.2018.07.38.


