俗话说得好,方差有三宝:独立、正态、齐性好。什么意思呢?就是说使用方差分析需要三个前提条件:1、各样本须是相互独立的随机样本;2、各样本来自正态分布总体;3、各总体方差相等,即方差齐。
纵然方差分析的用途广泛,可以不受比较组数的限制,进行多组比较。然而在实际的数据分析中,我们辛苦收集的数据往往很难符合其使用的条件。但我们又需要从样本数据中,获得尽可能多的信息,此时使用非参数检验就再适合不过了。
非参数检验类别
按照样本数量分类,可以将非参数检验方法分为几个方面:
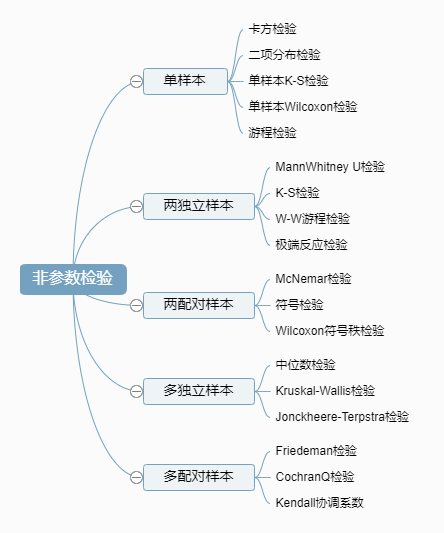
单样本非参数检验方法
卡方检验:用于分析定类数据与定类数据之间的关系情况,例如不同减肥治疗方式对于减肥的帮助情况(胆固醇水平)。卡方检验用于研究X和Y之间的关系,且X,Y均为定类数据。并且卡方检验需要使用卡方值和对应P值去判断X与Y之间是否有差异。通常情况下,共有三种卡方值,分别是Pearson卡方,yates校正卡方,fisher卡方;优先使用Pearson卡方,其次为yates校正卡方,最后为fisher卡方。
二项分布检验:是指在只会产生两种可能结果如阴性、阳性之一的n次独立重复试验(常常称为n重Bernoulli试验)中,每次试验的“阳性”概率保持不变时,出现“阳性”的次数X=0,1,2......n的一种概率分布。在医学研究中较为常用。
单样本K-S检验:单样本K-S检验能够利用样本数据推断样本来自的总体是否服从某一理论分布(正态分布,均匀分布,泊松分布,指数分布)。适用于探索连续型随机变量分布。
单样本Wilcoxon检验:(也称单样本wilcoxon符号秩和检验,符号秩和检验,也或者秩和检验等);其被用于检验数据是否与某数字有明显的差异性。首先需要判断数据是否呈现出正态性分析特质,如果数据呈现出正态性特质,此时应该使用单样本T检验进行检验;如果数据没有呈现出正态性特质,此时应该使用单样本Wilcoxon检验。
游程检验:游程检验用于检验数据是否具有随机性,其原始假设是数据序列不具有随机性;如果检验结果显示P值小于0.05,则说明数据不具有随机性,反之P值大于等于0.05则说明数据具有随机性。如果数据有上升或下降的趋势,或有呈周期性变化的规律等特征时,均可能表示数据与顺序是有关的,或者说序列不是随机出现的。通俗来讲,游程检验是用于分析数据是否为随机。
两独立样本非参数检验方法
MannWhitney U 检验:是用得最广泛的两独立样本秩和检验方法。用于研究定类数据与定量数据之间的关系情况。例如研究人员想知道不同性别学生的购买意愿是否有显著差异,如果购买意愿没有呈现出正态性特质,此时建议可使用MannWhitney U 检验。其原假设是:两独立样本来自的两总体的分布无显著差异。
W-W游程检验:用来检验两独立样本来自的两总体的分布是否存在显著差异。通过分析游程的大小和数量实现游程检验,从而判断两组样本在混合序列中的排列是否为随机的。若两组样本在混合序列中的排列是随机的,则两组样本之间没有显著性差异。
极端反应检验:从另一角度检验两独立样本所来自的量总体分布是否存在显著性差异。其基本思想是:将一组样本作为控制样本,另一组样本作为实验样本。以控制样本作为对照,检验试验样本相对于控制样本是否出现了极端反应。如实验样本没有出现极端反应,则认为两总体分布无显著差异,相反则认为存在显著差异。
两配对样本的非参数检验方法
McNemar检验:用于两配对样本的分析,其将研究对象自身作为对照者检验其“前后”变化是否有显著差异,例如比较同一批观测对象用药前后或实验前后的结果有无差异。该检验只适用于二分变量,即只有两种可能“是”或“否”,“阳性”或“阴性”,“有反应”或“无反应”等,对于非二分变量,应在分析前进行数据变换。
符号检验:也是用来检验配对样本所来自的总体的分布是否存在显著性差异的非参数方法。符号检验法是通过两个相关样本的每对数据之差的符号进行检验,从而比较两个样本的显著性。由于这种方法只考虑符号,不考察差数的大小,因而失去样本所提供的一部分信息,准确度不高。因此除了小样本,一般不使用符号检验。
配对样本Wilcoxon检验:配对样本Wilcoxon检验用于检验配对数据是否具有显著性差异,比如实验组和对照组的成绩差异性,手术前和手术后的体重差异性。从功能上讲,配对样本Wilcoxon检验与配对样本T检验完全一致,区别仅在于数据是否正态。
多独立样本的非参数检验方法
中位数检验:用来检验多个独立样本来自的总体的中位数是否存在显著差异。其基本思路:先求取混合后数据的中位数,然后利用卡方分布统计量来计算每个样本组内中位数两侧个案数的差异性。
K-W检验:用于检验多个总体的分布是否存在显著差异。SPSSAU会自动选择MannWhitney或者Kruskal-Wallis统计量。如果X的组别为两组,比如男和女共两组,则应该使用MannWhitney统计量,如果组别超过两组,则应该使用Kruskal-Wallis统计量结果。
多个配对样本非参数检验方法

如果是多相关样本,并且目的在于研究差异性,则有Friedeman检验和CochranQ检验两项可用,但特别提示一点,CochranQ检验涉及的数据一定是二分类(即1和0这样的数据);如果是研究多相关样本的一致性情况,则可使用Kendall协调系数。
参数或非参数的正确选择
选择参数检验或非参数检验需要结合专业情况以及数据类型数据形态,综合参数检验和非参数检验的优缺点进行考量,方法的选择没有绝对意义上的标准答案。
参数检验假定总体分布服从正态或近似正态,如果数据服从正态分布,参数检验是最好的选择。如果不满足这些条件的情况下,依然使用参数检验分析,很可能让检验结果产生错误。而非参数检验不受数据分布的限制,检验条件比较宽松,对于总体未知的样本都可以适用。但非参数检验也存在不足,非参数检验对总体假定不多,因而会缺乏针对性,功效不如参数检验。
同时样本的数量也影响着选择何种方法。一般来说小样本用非参数检验,大样本采用参数检验。原因是参数检验假定了服从某种分布,当样本量过小时,无法识别数据分布状态,而非参数检验对样本量没有要求,因此可选择非参数检验。


