批次效应（batch effect）

一、定义

下面是大佬给出来的关于批次效应(batch effect)的定义：

Batch effects are sub-groups of measurements that have qualitatively different behaviour across conditions and are unrelated to the biological or scientific variables in a study. For example, batch effects may occur if a subset of experiments was run on Monday and another set on Tuesday, if two technicians were responsible for different subsets of the experiments, or if two different lots of reagents, chips or instruments were used. Leek et. al (2010)

批次效应是测量结果中的一部分，它们因为实验条件的不同而具有不同的表现形式，并且与我们研究的变量没有半毛钱关系。一般批次效应可能在下述情形中出现：

• 一个实验的不同部分在不同时间完成；
• 一个实验的不同部分由不同的人完成；
• 试剂用量不同、芯片不同、实验仪器不同；
• 将自己测的数据与从网上下载的数据混合使用；
• ……

二、检测

批次效应相关协变量已知时，直接聚类观察结果是否和相应协变量相关。
混合数据因为实验条件迥异，一般批次效应都很大。

以R为例，通过聚类检验是否存在批次效应。请先查看下面的示例数据集。

# t() 转置函数
# dist() 距离函数：按照指定规则求行向量间的距离，因此要转置
> dist_mat <- dist(t(edata))
> clustering <- hclust(dist_mat) # hclust 的输入结构与 dist 相同！
# 按照批次信息聚类
> plot(clustering, labels = pheno$batch)
# 按照是否是正常细胞聚类
> plot(clustering, labels = pheno$cancer)

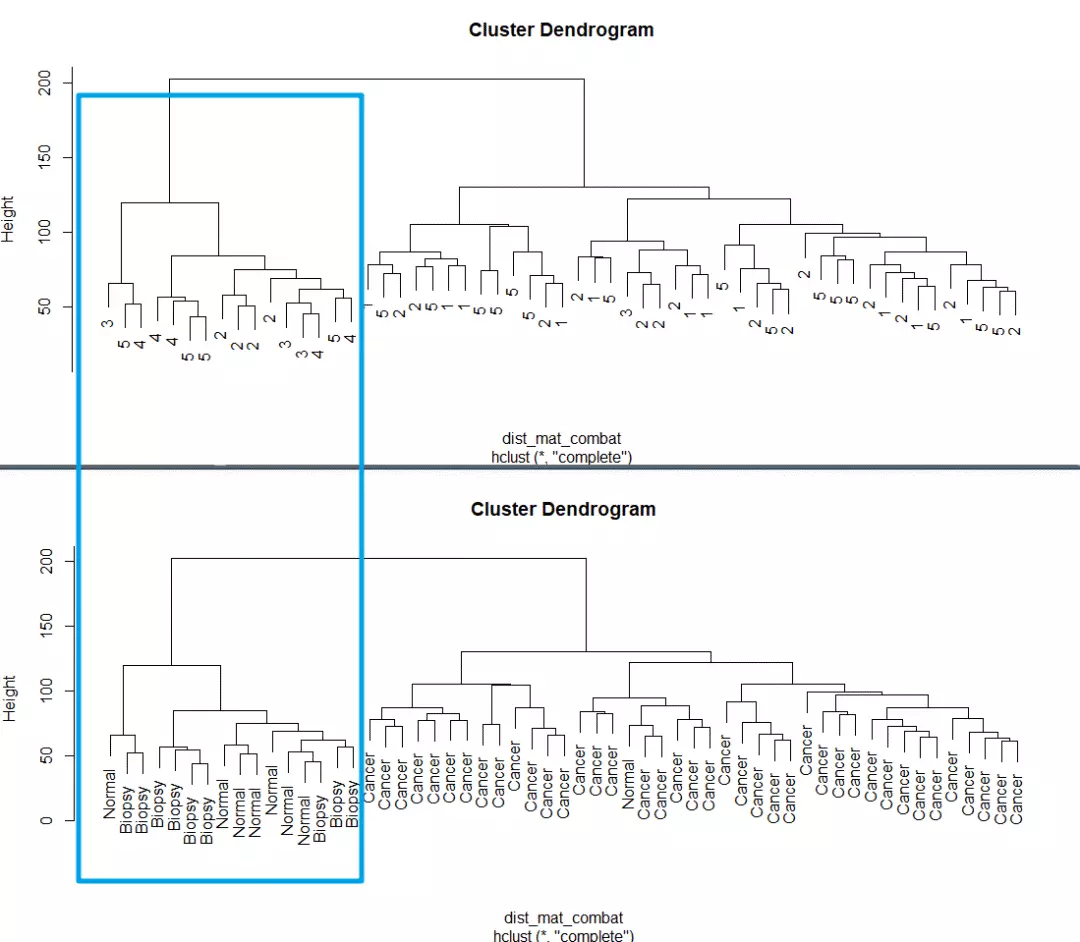
聚类结果如下：

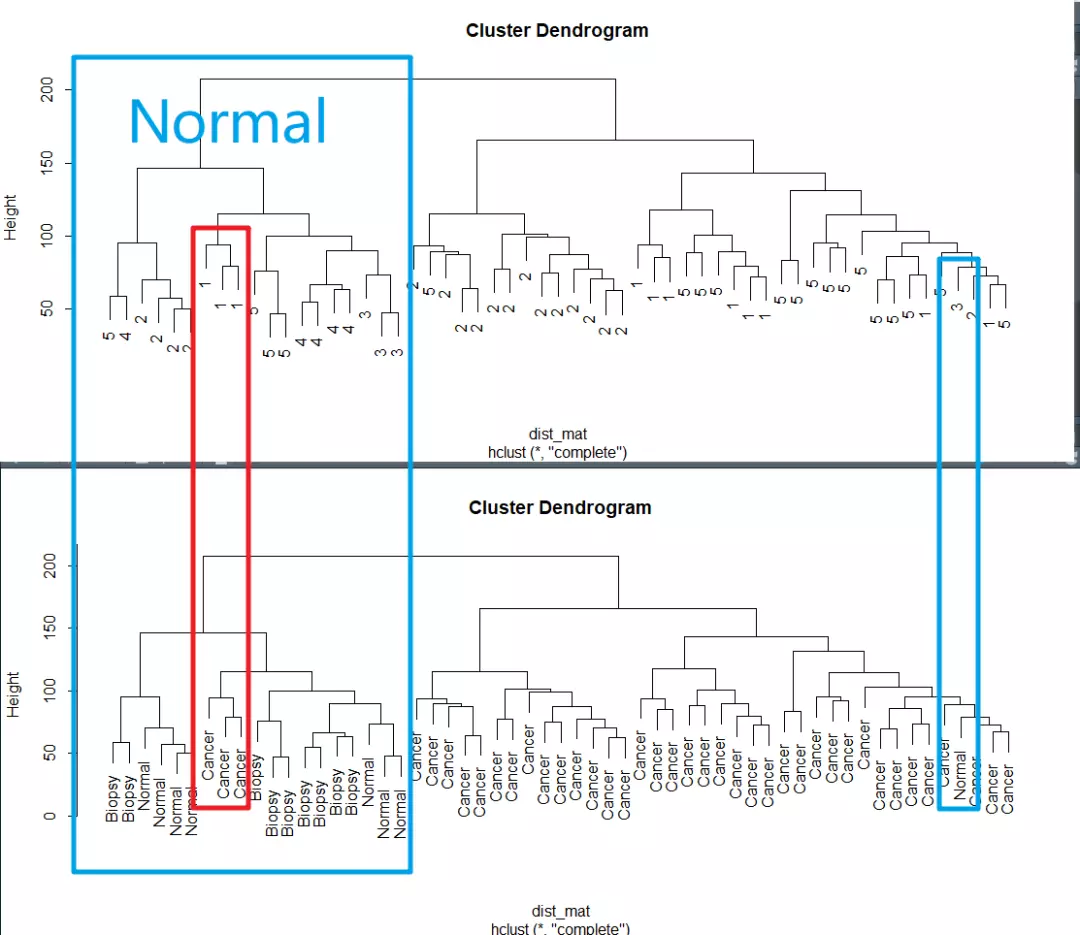
左边的红色框框是正常细胞中混入的癌细胞，右边蓝色框框中是癌细胞中混入的正常细胞。

还有许多检验批次效应的的方法，这篇文章给出了多种检验方式：

• 图分析：双柱状图、QQ图、箱线图、块图、…
• 定量分析：F检验、双样本t检验、…

三、处理

实验条件允许的条件下，应该优化实验设计，将引起批次效应的协变量采样分散开来。例如，对于时间批次效应，实验的不同部分应该在各个时间内均匀采样。这叫“治病就治本”。

但是大多数情况下实验条件不允许，如果够幸运的话批次效应相关的协变量已经被记录下来了，此时对批次效应进行验证，然后使用统计模型过滤；如果十分不幸，批次效应相关的协变量没有被记录或者不明显，我们就需要借助相关工具猜一下哪个变量可能造成了批次效应，然后使用统计模型过滤。前者叫参数化方法，后者叫非参数化方法。

1.导入示例数据集

bladderbatch包

bladderbatch包包含了一项膀胱癌研究中相关的57个样本的基因表达数据，这些数据已经使用RMA标准化，并且已经按照相关协议进行了预处理。

另外阅读R文档我们发现：

• eSet是一个包含高通量实验元数据的一个类，它不能直接被实例化。
• pData方法在类eSet中被定义，它的作用是访问数据的元数据（注释信息）。
• ExpressionSet继承自eSet，同样是一个高通量测序数据的容器，由> * biobase包引入，封装了表达矩阵和样本分组信息。表达矩阵存储在exprs中。

bladderbatch数据集是（类似）ExpressionSet类型，我们可以使用pData()加载元数据，使用exprs()加载表达谱数据。
bladderbatch数据集用来演示如何校正批次效应。

下载和加载数据集

## 1.安装并加载数据集
> BiocInstaller::biocLite("bladderbatch")
> library(bladderbatch) # 或者 library("bladderbatch", character.only=TRUE)
## 2.查看当前可用数据集
> data()
## 3.检查是否有如下信息
Data sets in package ‘bladderbatch’:
bladderEset (bladderdata)           Bladder Gene Expression Data Illustrating Batch Effects
## 加载数据集
> data(bladderdata) # 实际加载进来的数据集名字叫做 bladderEset !
> pheno <- pData(bladderEset) # 使用 pData 加载元数据/注释信息
> edata <- exprs(bladderEset) # 使用 exprs 加载数据

pheno如下所示：

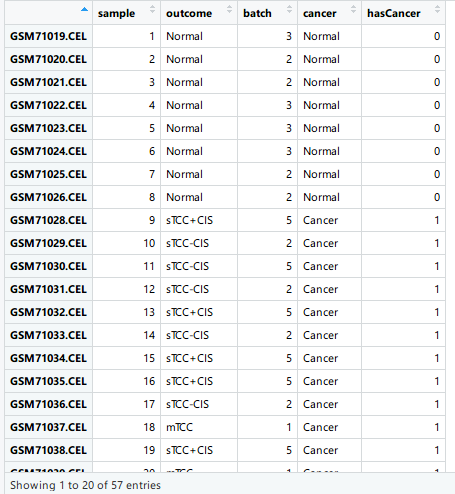
样本的批次信息存储作为元数据存储在pheno$batch中（R中使用$访问对象的属性）。

edata如下所示：

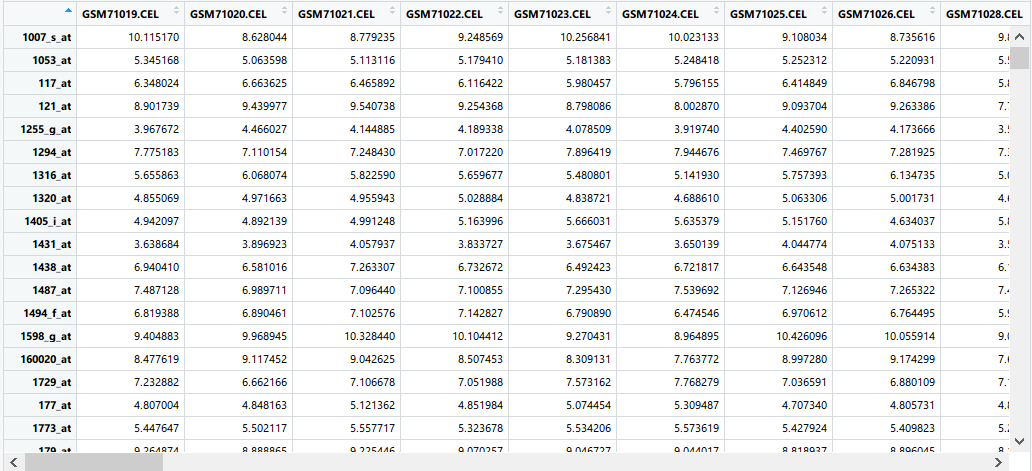
一列表示一个样本（细胞），后面求距离需要转置。

2.R中的sva包

sva用于移除高通量测序数据中的批次效应以及其它无关变量的影响。

sva包含用于标识和构建高维数据集（例如基因表达、RNA测序/甲基化/脑成像数据等可以直接进行后续分析的数据）代理变量的函数。代理变量是直接从高维数据构建的协变量，可以在后续分析中用于调整未知的、未建模的或潜在的噪音源。

代理变量（surrogate/proxy variable）: A variable that can be measured (or is easy to measure) that is used in place of one that cannot be measured (or is difficult to measure). For example, whereas it may be difficult to assess the wealth of a household, it is relatively easy to assess the value of a house. See also proxy variable. (from Oxford Reference)
代理变量分析（Surrogate Variable Analysis）：Click here

sva从三个方面消除人为设计造成的影响：

1. 为未知变异源构造代理变量；(Leek and Storey 2007 PLoS Genetics, 2011 Pharm Stat.)
2. 使用ComBat直接移除已知的批次效应；(Johnson et al. 2007 Biostatistics)
3. 使用已知的控制探针(known control probes)移除批次效应；(Leek 2014 biorXiv)
   移除批次效应和使用代理变量可以减少依赖性，稳定错误率估计值，提高重现性。

查看sva在线文档。

> 已记录批次信息

当批次协变量已知时（即每个样本分属于哪一个批次记录在数据集的元数据中），可以使用sva的ComBat校正批次效应。
ComBat使用参数（parametric）或者非参数（non-parametric）的经验贝叶斯框架（Empirical Bayes Frameworks）进行批次效应的校正。

先看ComBat的用法：摘自官方文档

> ComBat(dat, batch, mod=NULL, par.prior = TRUE, prior.plots = FALSE)
# dat: 基因组测量矩阵（探针维度 X 样本数），探针维度例如marker数、基因数.....，例如表达谱矩阵
# batch: 批次协变量，只能传入一个批次协变量！
# mod: 这是一个模式矩阵，里面包含了我们感兴趣的变量！
# par.prior: 基于参数/非参数，默认为基于参数

有了背景知识我们就可以进行膀胱癌数据的批次校正：

> pheno$hasCancer <- pheno$cancer == "Cancer"
# 或者 > pheno$hasCancer <- as.numeric(pheno$cancer == "Cancer")
> model <- model.matrix(~hasCancer, data=pheno)
> combat_edata <- ComBat(dat = edata, batch = pheno$batch, mod = model)
# 这里的 mod 参数就比较有意思了，它记录的是我们感兴趣的变量。因为初次接触R只能肤浅理解一下。
# 它应该是一个我们期望样本能被正确聚类所依据的协变量，它总是数值型变量

model.matrix(...)的详细解释见这里。

画图：

> dist_mat_combat <- dist(t(combat_edata))
> clustering_combat <- hclust(dist_mat_combat, method = "complete")
> plot(clustering, labels = pheno$batch)
> plot(clustering, labels = pheno$cancer))

我们发现批次效应被移除了：

> 没有记录批次信息

看这里

3.R中的ber包

ber的全称就是batch effects removal，使用> install.packages("ber")安装ber包，查看用户手册。

这个包里有6个函数，它们的作用就是校正微阵列标准数据中的批次效应。标准数据指的是：输入矩阵每一行代表独立的样本，每一列代表基因；批次信息作为已知的分类变量；期望变量可以大大提高批次效应校正的效率。

上表中的：

• Y是输入矩阵（样本数 n×gn×g 探针数）
• b是 nn 维分类1向量，每个分量对应着每个样本的批次信息
• covariates是一个 nn 行的data.frame实例

上面的6个函数都需要指定b，所以它们都是用来处理批次信息被记录的情形的，对于启发性的校正貌似没提出解决方案。

4.R中的RUVSeq包

RUVSeq means Remove Unwanted Variation from RNA-Seq Data, which shows us how to conduct a differential expression (DE) analysis that controls for “unwanted variation”, e.g., batch, library preparation, and other nuisance effects, using the between-sample normalization methods proposed in Risso et al. (2014).

RUV算法基本原理参考这里，原文在这里。

5. R中的BatchQC包

BatchQC工具

四、FAQ

1. 标准化（normalization）可以消除批次效应吗？ 只能缓解，不能消除。

五、其它资料

Stanford大学MOOC公开课讲义：PH525x series - Biomedical Data Science

TCGA Batch Effects Viewer

From BioMedSearch: Removing batch effects in analysis of expression microarray data: an evaluation of six batch adjustment methods.