理解ROC和AUC

来源：Kai评论4,674

ROC和AUC平时用的比较多，但是其真正的原理和计算过程却了解的不多，因此做个整理

照抄自网上的一个例子，加深下理解：

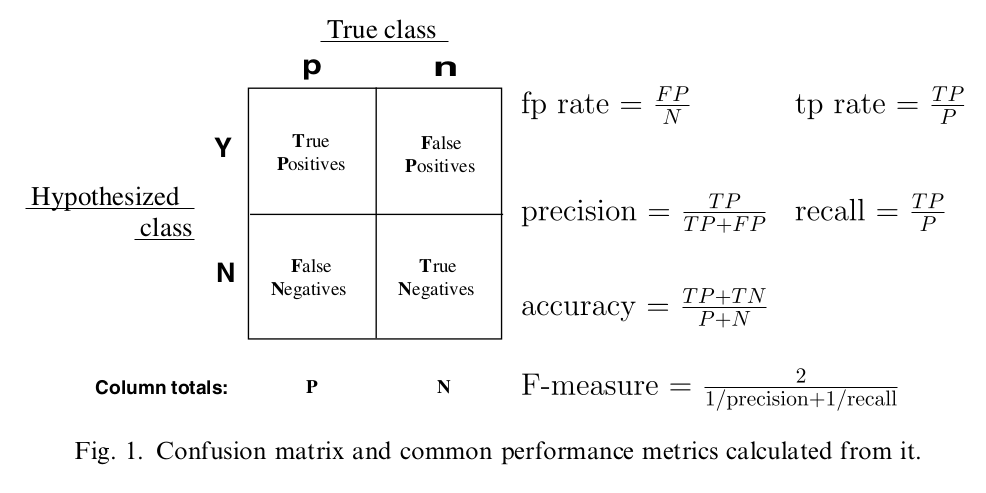
比方说在一个10000个人的数据集中，有100个人得了某种病症，你的任务是来预测哪些人得了这种病症。你预测出了200人得了癌症，其中： * TN，True Negative：没有得癌症并且你也预测对没有得癌症的有9760人 * TP，True Positive：得了癌症而且你也预测出来的病人有60人 * FN，False Negative：得了癌症但是你没有预测出来的病人有40人 * FP，False Positive：没有的癌症但是你预测得了癌症的有140人

那么：

  • True Positive Rate(TPR): 60/(60+40)=0.6
  • False Positive Rate(FPR): 140/(9760+140)=0.0141
  • accuracy: (9760+60)/10000=0.982
  • precision: 60/(60+140)=0.3
  • recall: 60/100=0.6 从上述例子可看出，几个重要指标的含义如下（盗图）:

理解ROC和AUC-图片1

简单的说，在上述癌症检测中（正反例极度不平衡的情况下），accuracy意义不大，从结果中可看出，因为正例比较少，所以检测再不怎么准确，其accuracy值都很高。recall则是相对于真实情况而言的，你正确检测了60例癌症病人，总癌症病人有100例，那么recall则为60%。precision则是相对于模型预测情况而言的，你预测了200例癌症病人，其中预测准确的有60例，那么precision则为30%；所以我们是希望能看到模型的recall和precision都很高，但是一般两者难以同时达到最优值，需要做一个权衡

有时我们还会见到sensitivity和specificity两个概念：

  • sensitivity = recall = True Positive Rate
  • specificity = 1- False Positive Rate

也就是说想要sensitivity高一点相当于要True Positive Rate高一点，要specificity高一点相当于False Positive Rate低一点

话说为了权衡recall和precision，对于评判二分类器的优劣，可以使用ROC(Receiver Operating Characteristic)曲线以及AUC(Area Under roc Curve)指标；ROC平时用的很多，其计算方式整理如下：

先清楚ROC曲线的几个概念，横坐标是FPR，纵坐标是TPR，而图中每个点则是不同”截断点”下计算的FPR和TPR，截断点相当于模型对于样本的概率输出，也可以说是打分score

理解ROC和AUC-图片2

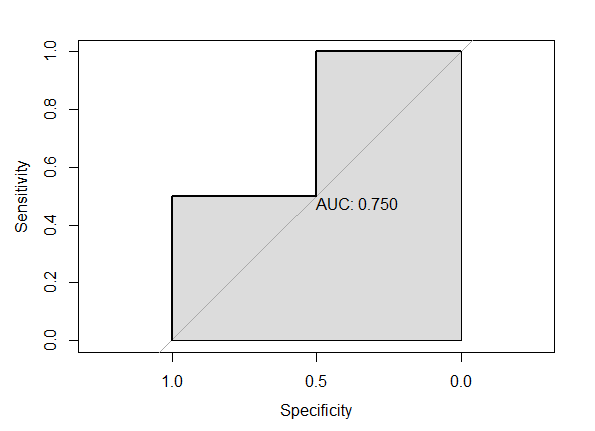
以一个简单的模拟数据来计算下ROC曲线每个点的值

  • 先有一组真实分类，比如0,1,0,1；然后一组模型预测的打分（概率），比如：0.2,0.3,0.5,0.8
  • 依据上述打分依次计算每个样本输出概率下的FPR和TPR
  • 首先截断点为0.2，当概率大于等于0.2时，则预测为正例，因此4个样本均为正例（1），这时的FPR=1，TPR=1
  • 接着截断点为0.3，因此当概率大于等于0.3时预测为正例，因此样本1预测为反例，样本2-4为正例，这时的FPR=0.5，TPR=1
  • 以上述方法计算截断点0.5和0.8，当为0.5时，FPR=0.5，TPR=0.5；当为0.8时，FPR=0，TPR=0.5

从上述计算方法可看出，ROC一般是只用于二分类器的预测评价；我们也可以用工具来检验下上述的计算结果，Python可以用sklearn，R可以用ROCR包或者pROC包，这里以ROCR包来检验下上述计算结果：

library(ROCR)
y <- c(0,1,0,1)
p <- c(0.2,0.3,0.5,0.8)
pred <- prediction(p, y)
perf <- performance(pred, "tpr", "fpr")
perf
> perf
An object of class "performance"
Slot "x.name":
[1] "False positive rate"

Slot "y.name":
[1] "True positive rate"

Slot "alpha.name":
[1] "Cutoff"

Slot "x.values":
[[1]]
[1] 0.0 0.0 0.5 0.5 1.0


Slot "y.values":
[[1]]
[1] 0.0 0.5 0.5 1.0 1.0


Slot "alpha.values":
[[1]]
[1] Inf 0.8 0.5 0.3 0.2

x.values对应FPR，y.values对应TPR, alpha.values对应预测打分cutoff，结果跟上面完全一致，然后简单做个ROC图，个人喜欢pROC包的图。。。

library(pROC)
modelroc <- roc(y,p)
plot(modelroc, print.auc=TRUE, auc.polygon=TRUE)

理解ROC和AUC-图片3

上述的图中的AUC值就相当于ROC曲线的所覆盖的面积，可以从ROC曲线看出AUC值越大，其分类效果越好；如果AUC等于0.5，则相当于做个预测结果跟随机的没啥差别

至于怎么计算AUC：

  • 从早期的计算ROC曲线下的面积
  • 现在的可以通过计算正例score大于反例score的概率；比如上面例子中正例有2个(M)，反例有2个(N)，那么总共有2*2=4对（[0.3,0.2],[0.8,0.2],[0.3,0.5],[0.8,0.5]）正反样本对，同时通过其模型预测的score可看出正例score大于反例的有3对（[0.3,0.2],[0.8,0.2],[0.8,0.5]），因此AUC则为3/4=0.75
  • 当样本比较多时，上述算法的复杂度过高O(N*M)，有人提出一个简单的算法：对score从到小排序，最大的score排序索引为n，最小的则为1；然后将正例的索引求和，减去正例-正例这种组合的个数M*(M+1)/2；最后除以M*N。以上述为例：正例的排序索引为2和4，M和N都为2，因此AUC=(2+4-2*(2+1)/2)/(2*2)=0.75

从上述可看出，只要理解了ROC和AUC的原理，其实计算方法都蛮简单的

参考资料：
AUC的计算方法及相关总结
ROC与AUC的定义与使用详解

发表评论

匿名网友