正态分布与方差齐性的检验方法与SPSS操作

来源：一统浆糊312,522

众多的参数检验方法都要求数据呈正态分布和方差齐性，本文介绍正态分布和方差齐性的常用检验方法及SPSS操作，但不涉及多元正态分布和方差-协方差齐同。

（1）数据分析前有没有必要做正态分布检验？大部分的统计教材案例都没有这个检验，是不是可以不做？正态分布（或者近似正态分布）是诸多参数检验的前提条件，没有这个前提，后续的判断也就没有了意义。正如你打算找一个女人做老婆，你可以通过各种描述、推断她的样子，但前提是她得是一个女人，如果不是女人甚至不是人，描述和推断结果无论你觉得如何完美都没有了意义。

（2）图示法显示数据差不多是正态的，计算检验法的Sig却小于0.05，是正态呢还是非正态？使用图示法怕别人质疑，毕竟计算法是定量的，可要是使用这个定量的方法，很多数据分布就不是正态了。曾经一段时间，只要发现数据不是正态，笔者就改用非参数分析方法来避开这个非正态的问题。至今笔者都觉得这样的处理没有什么本质的错误，只是可能选择了不是最合适的方法而已。这样做的结果也是有代价的，那就是错了诸多统计先辈发现的能说明更多问题的分析模型。

其实世上几乎没有变量是绝对呈正态分布的，但是常用的统计学方法都可以耐受数据在一定程度上的偏离，因此并不影响最终的结果，正如牛顿的经典力学，放到爱因斯坦相对论的体系里面，只能算是近似等于，可我们还是可以靠着经典力学把卫星送上了太空。总之，差不多符合就可以了，不要太较真。大部分的统计教材根本不做这个检验，可能是由于分析的案例数据的总体分布现实生活中普遍认为是正态的，还有就是考虑到这个结果的稳健性，当然也可能洛阳纸贵以至于出版商没有纸张做这些印刷了。

由于正态分布的计算检验法在样本太小时太不敏感，样本稍大又过于敏感，真要较真，感觉正态的数据也不正态了。图示法虽不能定量评估，但它不仅仅是计算法的一种补充，而是一种直观、简单、实用、有效的好方法。

同正态分布检验类似，方差分析对等方差的要求也具有稳健性。只要各组样本含量相等或者相近，即使方差不齐，方差分析仍然稳健且检验效能较高。样本含量相差较大，则Ⅰ类错误概率将明显偏离检验水准α。较大方差组有较大样本含量，分析结果较易拒绝H0，较大方差组有较小样本含量，分析结果较不容易拒绝H0。

一、正态分布检验

从经验上看，用样本中位数M与算术平均值的比值和算术平均值与标准差的关系进行判断，反映峰形和峰态：0.9＜中位数/均数＜1.1且 均数＞3倍标准差。如果以上关系成立，则可认为样本大致成正态分布。

正态检验方法分计算检验法和图示法。

计算检验法：K-S检验（Kolmogorov-Smirnov检验）、W检验（Shapiro-Wilk W检验）、W’检验（Shapiro-Francia检验）、D检验（D’Agostino）、偏峰度（常用矩法）、χ2拟合优度检验等

图示法：概率图（P-P图）、分位图（Q-Q图）、正态分位图、茎叶图、直方图、箱线图

SPSS示例：降压药Labe和Meto降压效果的基线（Group：1=Labe，2=Meto；Dbl：舒张压基线血压）

（1）K-S检验

SPSS中有两个地方可以做K-S检验，一处在“分析(Analyze) >> 非参数检验(Nonparametric tests)>>单样本(One sample)”，另一处在“分析(Analyze)>>描述统计量(Descriptive Statistics)>>探索(Explore)”中。两者的检验方法不同，检验结果可能也会有差异。单样本检验是将变量的观察累积分布函数与指定的理论分布进行比较，该理论分布可以是正态分布、均匀分布、泊松分布或指数分布，是一种拟合优度检验，检验效率较低。Explore中的K-S和W检验是用一个综合指标来反映材料的正态性，资料的正态峰和对称峰两个特征有一个不满足正态性要求时，假阴性较大。

单样本K-S检验统计量为Z，Explore分析中的K-S检验统计量为D。

①分割文件：数据(Data)>>分割文件(Split File)：将分组变量选入分组文本框即可，本例为Group

分析前要看数据结构，如果不同的分组使用同一个变量，则需要分割文件，将结果按组输出。如每个组是一个变量，则无需分割文件。注意区分右上侧单选的意义，默认是不拆分文件，第二项各组分析结果放在一起（同一张表格）中输出以方便比较，第三项各组结果单独输出。

②分析(Analyze)>>非参数检验(Nonparametric tests)>>单样本(One sample)

  • 字段(Fields)框：将需要检验的统计量放入检验字段(Test Fields)中，本例为Dbl
  • 设置(Settings)框：
  1. 选择检验方法(Choose Tests)：自定义检验(Customize tests)
  2. 选K-S法
  3. 选项(Options)按钮…假设分布(Hypothesized Distributions)对话框，选择正态分布(Normal)

③步骤②也可采用旧对话框：分析>>非参数检验>>就对话框(Legacy Dialogs)>>单样本K-S检验(1-Sample K-S)：将要检验的字段Dbl放入“测试变量列表(Test Variable List)”中，选中“检验分布(Test Distribution)”中的“正态(Normal)”即可

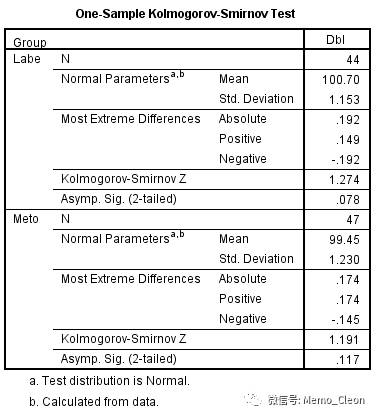
笔者比较喜欢旧对话框的结果，因为旧对话框的结果可以直接告知检验统计量，如单样本的K-S检验检验统计量为Z。旧对话框显示结果如图：Labe组，Z=1.274，P=0.078；Meto组，Z=1.191，P=0.117。不拒绝正态分布的假设，认为两组数据均呈正态分布。此处应注意标识“a 检验分布为正态分布”，笔者的理解是后面的均数和标准差在正态分布的时候才有意义。

正态分布与方差齐性的检验方法与SPSS操作-图片1

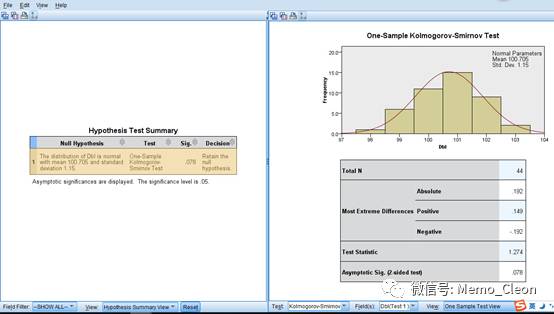
不用旧对话框的结果如下（仅以Labe组为例），结果是对模型假设的结论，P=0.078，保留无效假设结果，数据呈正态分布。双击即可看到更详细的结果，包括频数图及检验统计量等，结果同旧对话框结果相同。

正态分布与方差齐性的检验方法与SPSS操作-图片2

正态分布与方差齐性的检验方法与SPSS操作-图片3

（2）K-S检验和W检验

Explore分析中的Kolmogorov-Smirnov检验统计量为D，Shapiro-Wilk检验统计量为W。此处的K-S检验是经过Lilliefors改进或纠正的结果。

分析(Analyze)>>描述统计量(Descriptive Statistics)>>探索(Explore)

  • 因变量列表(Dependent List)：要分析的变量，可选入多个变量。本例为舒张压基线Dbl
  • 因子列表(Factor List)：分组因素，可选入多个变量。本例为Group
  • 绘制按钮(Plots)：可选择茎叶图、直方图、正态性检验(Normality plots with tests，带检验的正态图)及方差齐性检验

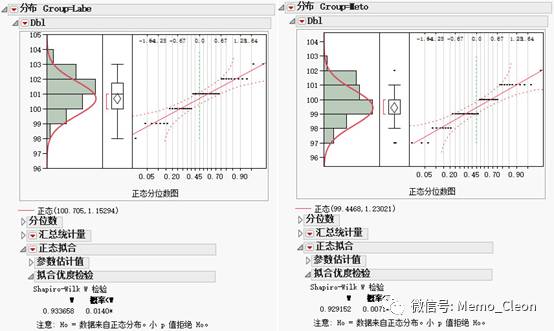
正态分布的检验结果如下，包括Kolmogorov-Smirnov和Shapiro-Wilk两种检验结果。结果显示两组两种方法的P均<0.05，拒绝原假设，数据不呈正态分布。本例样本数都不足50例，宜以Shapiro-Wilk结果为准（Labe：W=0.934，P=0.014；Meto：W=0.929，P=0.007）。此两种方法检验结果与单样本非参数K-S结果相左，但P值均接近0.01，结合图示法，数据呈近似正态分布。

正态分布与方差齐性的检验方法与SPSS操作-图片4

普遍认为Kolmogorov-Smirnov检验是大样本（N＞2000）下更容易成功接收正态性假设的一种检验方法。SPSS软件自带帮助规定Shapiro-Wilk检验统计量非整数权重数据样本可在3-50之间；无权重或者整数权重数据，样本量可在3-5000之间（If non-integer weights arespecified, the Shapiro-Wilk‘s statistic is calculatedwhen the weighted sample size lies between 3 and 50. For no weights or integerweights, the statistic is calculated when the weighted sample size lies between3 and 5000）。

本例用到了Explore探索分析，探索分析的功能计算常用的描述有统计量（如均值及置信区间，方差、标准差、偏度、峰度、极端值、百分位数等）、正态分析、方差齐性分析、绘制箱图、茎叶图和直方图。

（3）偏度、峰度

SPSS很多地方可以计算偏度（Skewness）系数和峰度（Kurtosis）系数，如：

注意频数过程和描述过程需要按组分割文件。数据>>分割文件，比较组：Group。Explore过程不需要分割。

  • 分析>>描述统计量>>频数(Frequencies)，将分析变量放入文本框，本例为Dbl。统计量(Statistics)按钮…分布(Distribution)：偏度、峰度
  • 分析>>描述统计量>>描述(Descriptives)，将分析变量放入文本框，本例为Dbl。选项(Options）按钮…分布(Distribution)：偏度、峰度
  • 分析>描述统计量>>探索(Explore)：因变量Dbl，自变量Group。默认有偏度系数、峰度系数数据

结果解读：

偏度是描述分布对称性程度和方向。Skewness=0，分布形态与正态分布偏度相同；Skewness>0，分布呈正偏态；Skewness<0，分布呈负偏态。

峰度是描述分布与正态曲线相比形态的陡缓/扁平程度。Kurtosis=0，与正态分布的陡缓程度相同（正态峰）；Kurtosis>0，比正态分布的高峰更加陡峭（尖峭峰）；Kurtosis<0，比正态分布的曲线更平坦（平阔峰）。

矩法检验使用μ检验检验偏峰度，检验统计量为μ。μs=偏度/偏度系数，μk=峰度系数/峰度标准误，结果与P=0.05时的检验统计量μ0.05=1.96，μ0.01=2.57~2.58。SPSS未提供该方法的计算（或者是我没找到@_@），感兴趣的可以手动计算。

本例仍以Labe组为例，K=-0.378，SE=0.702；S=-0.146，SE=0.357。μs=-0.54，P>0.05；μk=-0.41，P>0.05。可以认为资料服从正态分布。

（4）概率图（P-P图）：实际积累概率与假定分布积累概率的符合程度，不仅用于正态分布。

①数据>>分割文件：按比较组分割文件

②分析>>描述统计量>>P-P图(P-P Plots)：将分析变量放入文本框即可，本例为Dbl

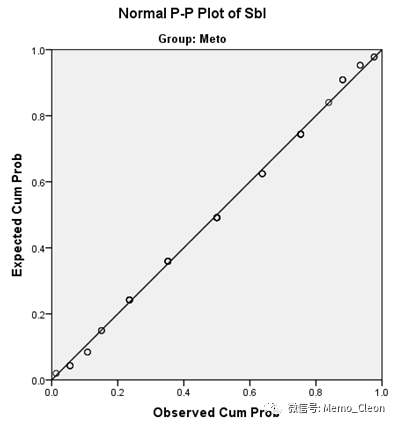
正态P-P图：横坐标为观测的积累频率，纵坐标为期望的积累概率。数据服从正态分布，则数据点基本集中在理论直线附近。如何算附近，笔者觉得SAS JMP正态分位图的做法很不错，可以借鉴，参见（6）JMP正态分位图。

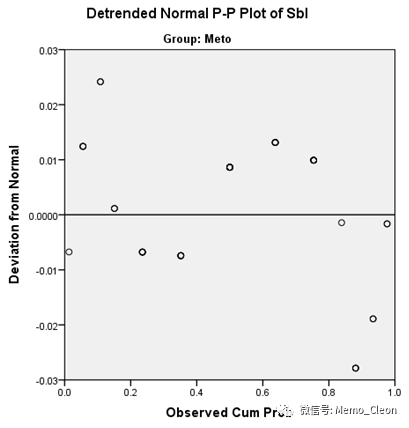
Detrended正态P-P图：理论值与实际值之差的分布，横坐标为观测的积累频率，纵坐标为正态偏差。数据服从正态分布则数据点均匀分布在Y=0的直线上下，绝对差值小于0.05（纵坐标）。

本例的舒张压P-P图显示，数据基本呈正态分布。

正态分布与方差齐性的检验方法与SPSS操作-图片5

正态分布与方差齐性的检验方法与SPSS操作-图片6

（5）分位图（Q-Q图）：实际百分位数与假定分布的理论百分位数的符合程度，Q-Q图操作及阅读基本同P-P相同，但比P-P图适应条件更宽松，结果更稳健，但不能像P-P那昂的经验界值来判断差异。

  • 分析>>描述统计量>>Q-Q图(Q-Q Plots)：将分析变量放入文本框即可，本例为Dbl。分析前按比较组分割文件：数据>>分割文件
  • 分析>>描述统计量>探索：因变量Dbl，自变量Group；绘制…带检验的正态图

（6）JMP正态分位图

SAS JMP图示法中的正态分位图：数据集中在直线附件，数据不超出95%置信区间线即可说明数据呈正态分布。

JMP步骤：

分析>>分布

Y，列：Dbl

分组依据：Group

正态分布与方差齐性的检验方法与SPSS操作-图片7

借鉴此种做法，可在SPSS的P-P图和Q-Q图上拟合95%置信区间，以此判断数据点是否在理论直线附近。

制作P-P图后，双击直方图进入图表编辑器：菜单栏元素>>总计拟合线(Fit Line at Total)：拟合线(Fit Line)

  • 拟合方法(Fit Method)：线性(Linear)
  • 置信区间(Confidence Intervals)：个体(Individual)

（7）  茎叶图：是否以钟形分布。

分析>>描述统计量>>探索(Explore)：因变量Dbl，自变量Group；绘制按钮(Plots)…茎叶图

茎叶图由三部分组成：叶子数（Frequency）、茎的大小（Stem）和叶子大小（Leaf）。图最下方还指出茎的宽度（Stem with）。（茎+每一片叶子数）×茎的宽度≈一个原始数据。

（8）直方图：是否以钟形分布，还可以选择输出正态性曲线

  • 分析>>描述统计量>>频数(Frequencies)，选择分析变量，本例为Dbl；图表(Charts)…直方图。选中“在直方图上显示正态曲线”复选框即可同时输出正态曲线。注意频数过程分析前按比较组分割文件：数据>>分割文件
  • 分析>>描述统计量>>探索(Explore)：因变量Dbl，自变量Group；绘制按钮(Plots)…直方图。双击直方图进入图表编辑器：菜单栏元素>>显示分布曲线，即可将各种分布曲线添加在直方图中
  • 残差直方图：分析>>回归(Regression)>>线性(Linear)
  • 因变量：分析变量，本例为Dbl；自变量：分组变量，本例为Group
  • 保存(Save)…预测值(Predicted Values)：标准化(Standardized)；残差(Residuals)：标准化(Standardized)
  • 绘制(Plots)…
  • 散点图(Scatter 1 of 1)：Y选入*ZRESID（标准化残差） |  X选入ZPRED（标准化预测值）
  • 标准化残差绘图(Standardized Residuals Plots)：选中直方图和正态概率图（P-P图）
  • 在通过“保存”生成标准化数据后，也可以不通过“绘制”，通过频数(Frequencies)过程也可以完成

（9）箱线图：主要观察离群值和中位数

分析>>描述统计量>>探索(Explore)：因变量Dbl，自变量Group；绘制按钮(Plots)…箱图(Boxplots)

二、方差齐性检验

方差齐性检验有F检验、Bartlett χ2检验、Levene检验、残差图。

F检验和Bartlett χ2检验要求数据资料具有正态性，Levence检验所分析资料可不具正态性，结果更为稳健。

Bartlett χ2检验检验统计量为χ2，F检验和Levene检验检验统计量为F。

（1）Levene检验

分析>>描述统计量>>探索(Explore)

  • 因变量列表(Dependent List)：要分析的变量，可选入多个变量。本例为Dbl
  • 因子列表(Factor List)：分组因素，可选入多个变量。本例为Group
  • 绘制按钮(Plots)…方差齐性检验(Spread vsLevel with Levene Test)：未转换

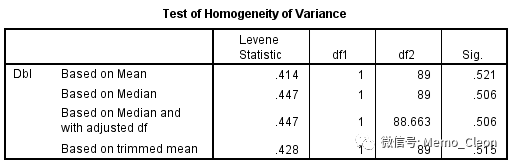
结果有4个：基于均值、中位数、基于调整自由度的中位数、基于截尾均值。其中基于均值的检验结果适用于正态分布，而中位数的结果适用于偏态数据，基于截尾均值的结果则适用于存在极端值的数据。上面的正态分布检验显示，Labe和Meto两组的Dbl数据呈（近似）正态，因此F=0.414，P=0.521,无统计学意义，可认为两组方差相等。

正态分布与方差齐性的检验方法与SPSS操作-图片8

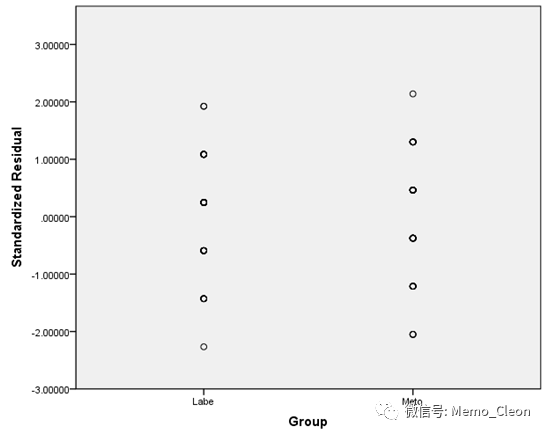
（2）残差图：直观判断多组定量资料的方差齐性。

操作过程：先生成标准化残差和标准化预测值，再制作标准化残差图。残差图以分组为横轴，标准化残差为Y轴制作散点图；或以各组预测值为X轴，标准化残差为Y轴制作散点图，可在散点图制作或线性回归中制作。

①分析>>回归(Regression)>>线性(Linear)

  • 因变量：分析变量。本例为Dbl
  • 自变量：分组变量。本例为Group
  • 保存(Save)…预测值(Predicted Values)：标准化(Standardized)；残差(Residuals)：标准化(Standardized)
  • 绘制(Plots)…
  • 散点图(Scatter 1 of 1)：Y选入*ZRESID（标准化残差） |  X选入ZPRED（标准化预测值）
  • 标准化残差绘图（Standardized Residuals Plots）：选中直方图和正态概率图（P-P图）

②图形(Graphs)>>图表构建器(ChartBulider)，确定

库(Gallery)字段：选择范围(Choose from)选择“散点图/点图(Scatter/Dot)”，将简单散点图(Simple Scatter)拖入预览框中，将分组变量或StandardizedPredicted Value[ZPR_1]拉入X轴，将Standardized Residual[ZRE_1]拉入Y轴

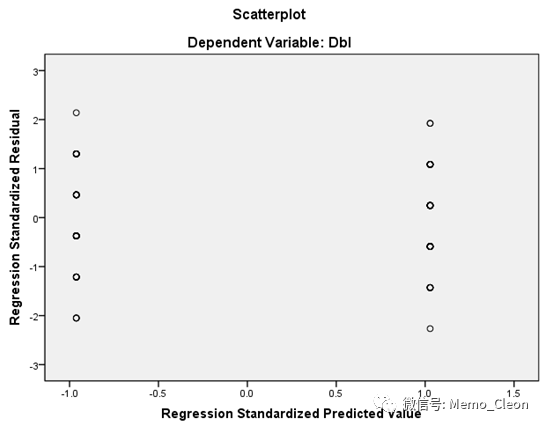
若散点随机地在残差为0的横线上下，且无任何特殊的结构，不存在异常点，则可认为符合方差齐性。【注：残差分析用在线性回归中用以深入了解实际资料是否符合回归模型的假设（正态性、等方差），还可用于识别离群点。±2倍标准化残差之间，模型数据拟合良好，±3倍标准化残差之外为离群点，±2~±3倍之间的可能为离群点】

本例散点在y=0的直线上下呈均匀分布可认为两组方差齐同，但个别数据出现在2-3倍标准差内，可能会与离群点。

正态分布与方差齐性的检验方法与SPSS操作-图片9

正态分布与方差齐性的检验方法与SPSS操作-图片10

评论  3  访客  0

发表评论

匿名网友

拖动滑块以完成验证