群殴之方差分析

本文介绍完全随机资料设计和随机区组资料设计的方差分析的SPSS操作，并介绍方差分析的适应条件。

方差分析（Analysis of Variance），字面翻译就是变异分析，也叫F检验，其基本思想就是根据试验设计类型将总变异进行分解，每个变异都可以用一个因素来解释（变异来源）。在H0假设成立的前提下（通常是假设各组相等），计算检验统计量F值，借助F分布获得 得到这个F值 的概率（P值）。这个概率可以通俗理解成H0成立的概率【修订：虽相等但因偶然造成此差异的概率】。如果概率很小，则认为H0假设是不成立的，则其对面成立的可能性很大（有统计学差异），这就是所谓的假设检验和小概率反证法思想。

按处理因素的多少，方差分析可以分为单因素方差分析（One-Way ANOVA）和多因素方差分析。完全随机设计资料常用单因素方差分析，SPSS采用的是One-Way ANOVA过程进行分析。多因素方差分析使用的是Univariate过程，常见的设计有析因设计、正交设计、裂区设计等。特别要说明的是因素是相对处理或者叫干预因素而言的，随机区组设计中的区组、交叉设计中的阶段、拉丁方设计中的行区组和列区组实际上并不是严格意义的“因素”，但在SPSS分析时将他们看作因素来对待，采用了Univariate过程，比如随机区组设计按处理因素、区组因素两个因素，交叉设计有处理因素和阶段因素，拉丁方设计有处理因素、行区组因素、列区组因素。

单因素还是多因素是以分类型自变量的多少为分类依据。按因变量的多少分类，则可分为单变量的方差分析和多元方差分析。Univariate为单变量的意思，单变量方差分析模型都可以采取Univariate过程，而不论是单变量单因素还是单变量多因素。单因素方差分析（One-Way ANOVA）只是多因素分析的一个特例而已。

（1）完全随机设计的方差分析

适用条件：独立性、正态性（各水平应变量服从正态分布）、方差齐性（各水平的总体具有相同的方差）。独立性要求样本中个元素相互独立，试验数据尽量做到随机化。方差分析对正态性的要求不高。轻微的方差不齐也不影响方差分析的结果，按照张文彤老师的说法，最大方差和最小方差比值小于3，分析结果都稳健。样本含量上的均衡可以弥补正态性和方差齐性得不到满足时对检验效能产生的影响。【注：理论上方差分析是以各单元格（各因素各水平的组合）为基本考察单位的，要求各组的随机误差项（模型残差）满足正态性和方差齐性，但实际操作时往往弱化成考察因变量的分布状态和变异程度。可参见本文最后张文彤老师关于方差分析的适应条件介绍】

单因素方差分析模型：Y=μ+α+ε。Y是因变量，不考虑α因素时的因变量值，α为α因素的效应，ε为随机误差项。

示例：降血脂新药的临床疗效。分组：安慰剂组和3个剂量组；疗效指标：低密度脂蛋白（LDL_C）测量值。

①正态性检验及方差齐性检验。方法很多，可参见“正态分布与方差齐性的检验方法与SPSS操作”。其中方差齐性检验也可以直接在单因素方差分析的选项中选择。

②分析>>比较均值(Compare Means)>>单因素方差分析(One-Way ANOVA)：将要分析的变量放入“因变量列表(Dependent List)”框，可选入多个变量同时分析，本例为LDL_C；分组变量放入“因素(Factor)”，本例为Group。

• 对比（Contrast）：用来设置趋势检验及事前计划比较。本例可选中“多项式（Polynomial）”复选框，度(Degree)选三次项（Cubic），目的是看下随着剂量的增加，低密度脂蛋白的变化趋势。本例4个组，最多可倍拆解为3次项进行分析；
• 多重比较（Pos Hoc）：设置两两比较的方法，是结果有统计学差异后进行的两两比较。本例选LSD、Bonferroni、Dunnett（多个试验组与一个对照组比较）、Tukey（各组样本含量需要相同）和Scheffe法；
• 选项（Option）：设置缺失值的处理方法、绘制均值图、查看的描述性统计量、方差齐性检验等。本例选中方差同质性检验、绘制均值图。

主要结果及解读：

• 正态性检验结果见下图，各组数据均呈正态分布。

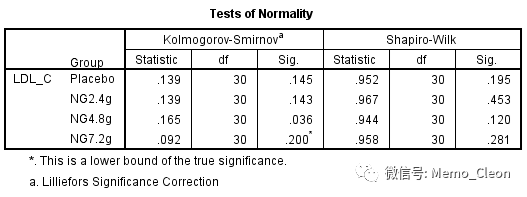
• 方差齐性检验F=1.622，P=0.188>0.05，方差齐性满足。

• 主要统计结果：分为组间效应和组内效应，其中组间效应又被分为线性项、二次项和三次项部分。如果在“对比”选项中不进行趋势检验则不会出现多项式检验结果。不同组间F=24.884，P<0.001，4组LDL_C差异具有统计学意义。趋势检验结果其中线性部分和三次项部分均有统计学意义（F=67.704，P<0.01；F=6.943，P<0.10），结合均值图，可以认为随着用药剂量的增加（安慰剂、2.4g、4.8g、7.2g），低密度脂蛋白的测量值呈线性下降。三次项部分也有统计学意义，变化趋势是先快速下降，然后缓慢下降，最后再快速下降，但个人以为数据点有限，不足以准确描述这种变化，毕竟这个世界已经很复杂了，能简单就简单一些吧。

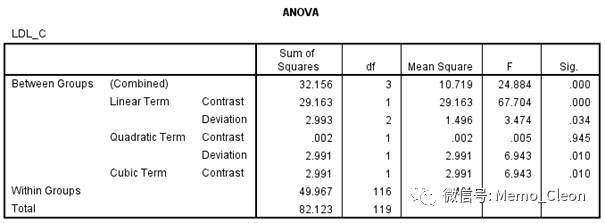
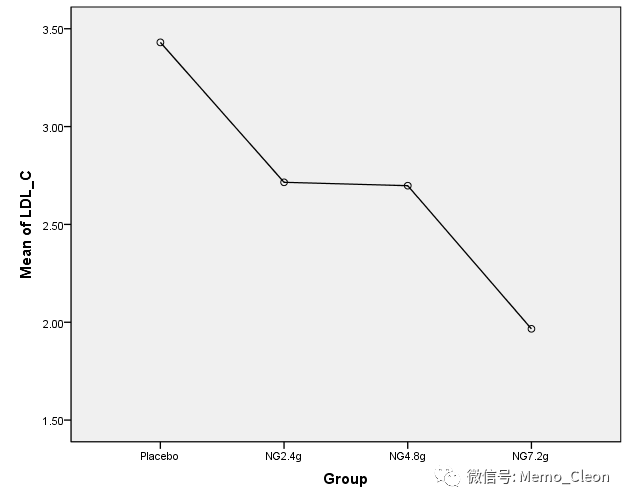
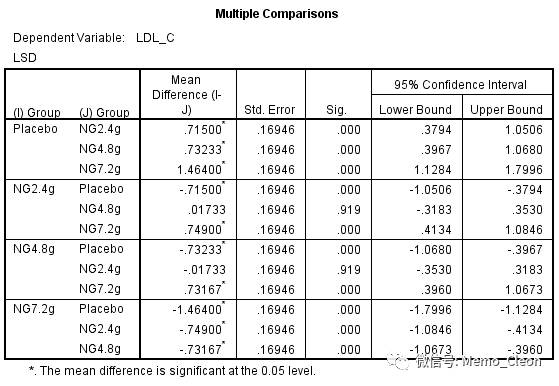
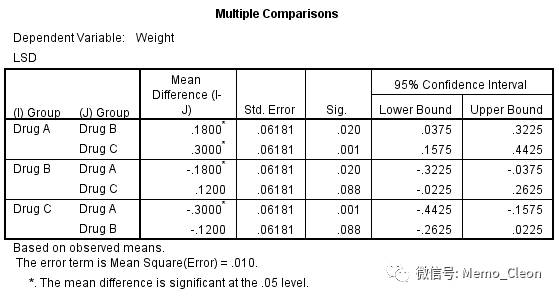
• 多重比较结果仅以LSD法结果为例，见下图。三个药物剂量组与安慰剂相比均具有统计学差异。在三个剂量组中，尚不能认为2.4g组和4.8g组有统计学差异（P=0.919）；2.4g组与7.2g组相比、4.8g组与7.2g组相比均有统计学差异。

（2）随机区组设计的方差分析

分析前无需考虑正态性和方差齐性，不是因为可以完全忽略，而是因为每个单元格只有一个元素而无法考察。必要时可以绘制残差图对残差进行分析。

两因素分析模型：Y=μ+α+β+(αβ)+ε。Y是因变量，不考虑α、β因素及其交互作用(αβ)时的因变量值，α为α因素的效应，β为β因素的效应，(αβ)为α和β的交互作用，ε为随机误差项。再次强调完全随机设计、随机区组设计、拉丁方设计和交叉设计不考虑交互效应只考虑主效应，即(αβ)=0。

示例：三种抗癌药物对小白鼠肉瘤的抑瘤效果。先按体重将15只小鼠分成5个区组（Block），每个区组的3只小鼠分别接受3中抗癌药物（Group）的治疗，以肉瘤重量（Weight）为指标。【注：小鼠体重从轻到重编号，体重相近的3只小白鼠配成一个区组，区组1-5体重逐渐增加】。

分析(Analyze)>>一般线性模型(General Linear Models)>>单变量(Univariate)：

将要分析的变量放入“因变量(Dependent Variable)”框，本例为Weight；影响因变量的各个因素放入“固定因素(Fixed Factor)”列表，本例有Group、Block。

是固定因素还是随机因素要根据分析目的来确定，如果结论仅针对分析因素中出现的水平，则为固定因素；如果需要外推至其他水平，则为随机因素。如果你看到一个大学生乱扔垃圾，结论是这个大学生素质真差，那么乱扔垃圾就是固定因素，但如果你的结论是现在的大学生素质真差，乱扔垃圾就应该按随机因素来处理。比如通过比较美托洛尔和替米沙坦治疗原发性高血压的疗效，目的就是比较美托洛尔和替米沙坦治疗高血压的疗效，药物分组就应该按固定因素来处理，但如果目的是比较以美托洛尔为代表的的β受体阻滞剂和以替米沙坦为代表的血管紧张素受体阻滞剂的疗效，那么药物分组就应该按随机因素来处理。

• 模型(Model)…默认指定模型（Specify Model）为全因素（Full factorial），全面分析各因素的主要效应及交互效应。随机区组设计不考虑考虑交互效应只考虑主效应。将要分析的因素添加到模型框中，本例指定模型（Specify Model）为自定义（Custom）；构建项（Build Term）构建类型（Type）为“主效应（Main effects）”，因素与协变量（Factors & Covariates）框中的“Group和Block”选入模型（Model）框中
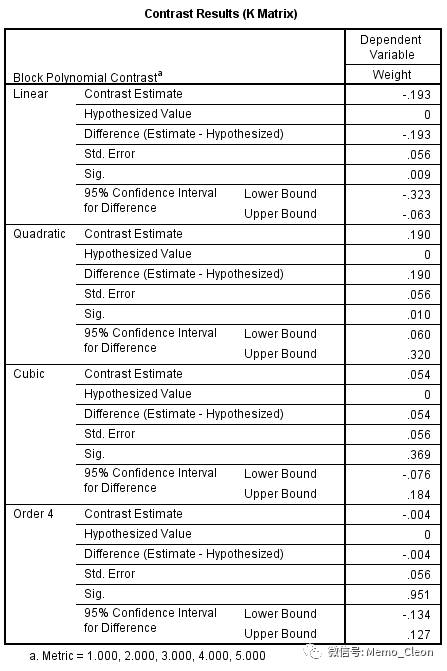
• 对比(Contrasts)…用于各因素不同水平的比较设置和变化趋势检验。本例组间因素比较趋势变化没有意义，但可以考察随着体重的增加（区组1-5），抑瘤效果的变化趋势。

• 绘图(Plots)…用于绘制轮廓图。常结合趋势检验查看变化趋势和交互作用。本例Group选入水平轴（Horizontal Axis），Block选入单独单图（Separate Lines），单机添加（Add）。单图（Separate Lines）与多图（Separate Plot）的区别是，单图是将因素的不同水平作在同一图中，而多图是将入选因素的各个水平单独作图。
• 多重比较(Post Hoc)…用于各因素不同水平间的两两比较。本例对Group和Block的各水平均进行两两比较。方法选择LSD。
• 保存(Save)…在数据库中产生残差、预期值等数据。本例忽略。
• 选项(Option)…估计边际均数、主效应比较、描述统计量方、差齐性检验、残差图等诸多内容。估计边际均数是剔除其他变量影响时算出的用于比较的各水平均值估计值，单因素模型和包含全部交互项的全模型，边际均值等于各样本均值，但含有协变量和去掉交互项的模型，边际均值和样本原始均值并不对应。若没有交互效应，各因素的作用可以直接用主效应来解释，但如果交互作用，主效应不能反应该因素的真实效应。因素和因素交互作用框中Overall是指估计所有样本的边际均数；后面是按各因素（本例有Grou和Block）估计边际均数。本例可将Group选入显示均数对话框中，也可以选中比较主效应的对话框。由于本例无交互效应，Group的估计边际均数和选中显示（Display）框中的描述性统计量（Descriptive statistics）中的均数是一致的，比较主效应的结果和多重比较(Post Hoc)的结果也是一致的。显示框中本例选中残差图（Residual Plot）。

主要结果及解读：

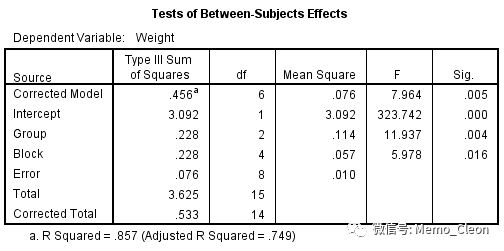
• 校正模型（Corrected Model）的检验是对整个方差分析模型的检验，H0假设是模型中所有因素对因变量无影响，即所有因素的系数均为0。F=7.964，P=0.005<0.05，模型有统计学意义，可以用该模型对各个因素进行分析。如该项P＞0.05，则意味着要考察的因素对结果没有影响，不合适用该模型进行分析。
• 截距（Intercept）为不考虑药物因素和区域因素的影响（影响=0）时的抑瘤效果，H0假设为不考虑药物因素和区域因素时，抑瘤效果为0。F=323.742，P<0.001，截距不为0。但在分析中没有实际意义，可以忽略。
• Group的F=11.037，P=0.004<0.05，可以认为三种抗肿瘤药的抑瘤不完全相同。
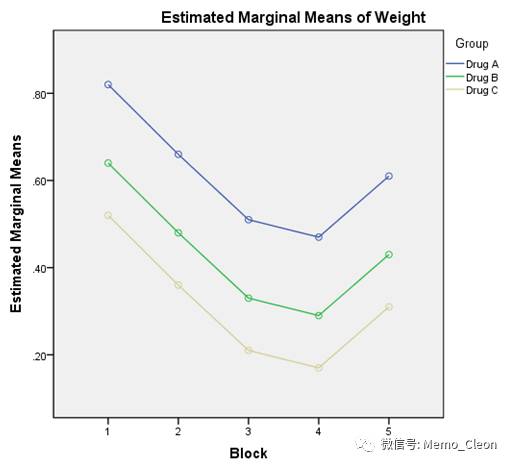
• 区组因素Block F=5.978，P=0.016<0.05，可以认为不同的区组抑瘤效果不完全相同。随着体重的增加（区组1-区组5），抑瘤效果呈线性递减趋势（P=0.009）或者先递减再递增二项式趋势（P=0.010），结合轮廓图，更符合先减后增的趋势。
• 注：校正总变异（Corrected Total）可分解为校正模型（Corrected Model）引起的变异和误差项（Error）引起的变异，其中校正模型引起的变异可分解为Group和Block之和。
  

• 多重比较结果：药物A和药物B、药物A和药物C之间的抑瘤效果均有统计学差异（P=0.20；P=0.01），药物B和药物C的抑瘤效果没有统计学差异（P=0.88）。Block多重比较结果分析与Group多重比较查看分析类型，篇幅原因省略。

• 边际均数估计及主效应比较结果略。
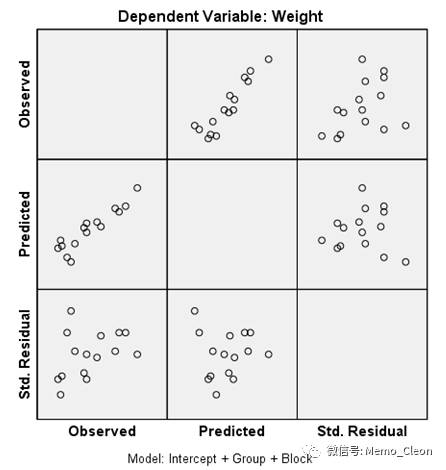
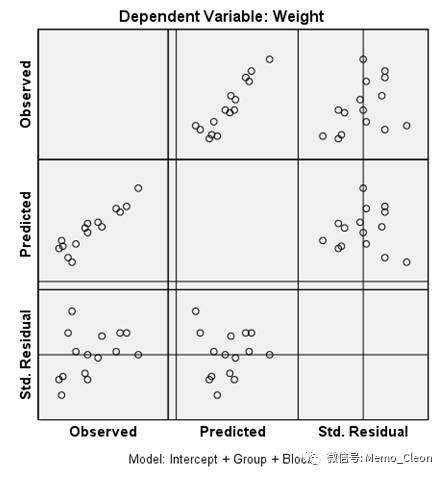
• 残差图结果如下图。双击残差图，进入编辑状态，添加X轴和Y轴的0线。编辑（Edit）>>选择X轴（Select X Axis）：在项目矩阵轴刻度（Martrix Axis Scal）中选中复选框“在原点处显示线（Display line at origin）”，即可显示X轴上的0线，同理选择Y轴，可显示Y轴0线。观测值和预测值呈现较好的线性趋势，标准残差随机在0线上下分布，说明模型的独立性、正态性和方差齐性较好。【注：预测值和观测值呈线性相关说明正态性较好；残差散点在0水平线上下随机均匀分布说明方差齐性较好；残差随着观测值的变化而变化说明独立性不好】

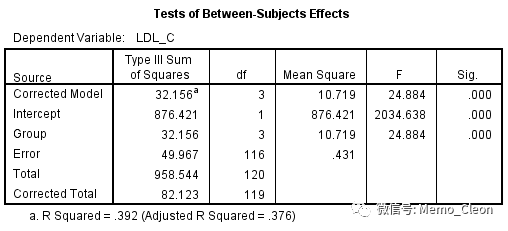
前面讲过单因素方差分析只是多因素分析的一个特例，所有单因素方差分析也可以使用Univariate过程，（1）中单因素方差分析示例用Univariate过程分析结果如下：F=24.884，P<0.001，同One-Way ANOVA过程分析结果完全一致。由于当前模型中只有Group一个因素，因此校正模型的统计学差异等同于Group间有差异。

 方差分析适应条件

张文彤,董伟.SPSS统计分析高级教程（第2版）[M].北京：高等教育出版社,2013.