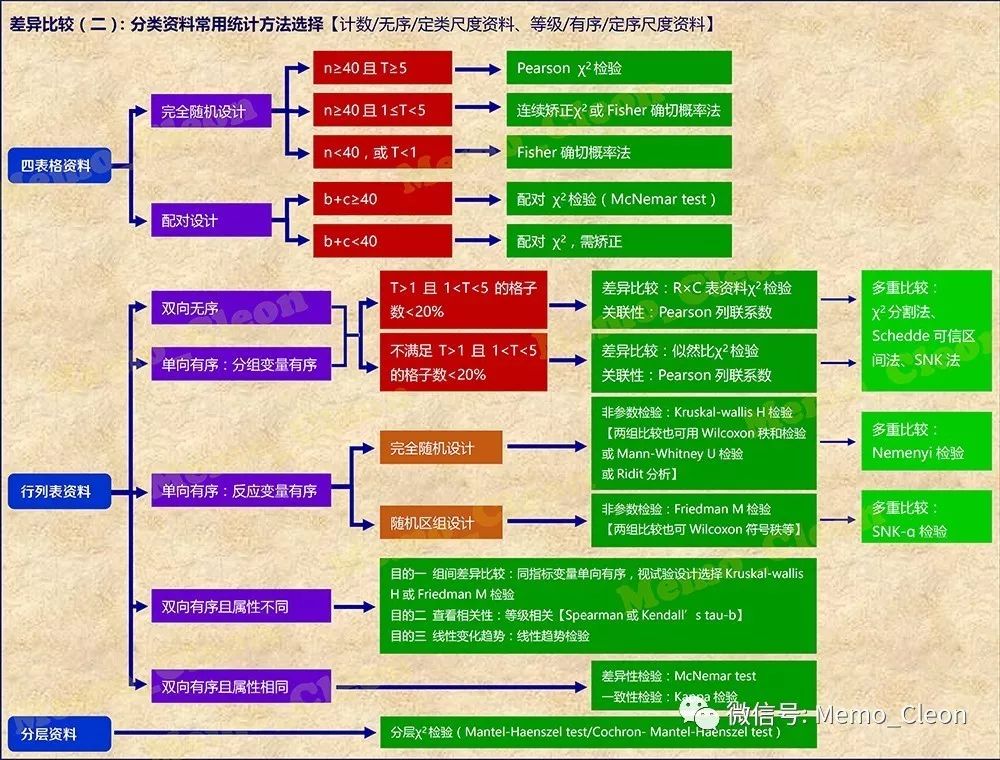
分类资料包括计数资料和等级资料,常用差异比较方法校正如下
本次笔记涉及内容:
(1)四表格资料的χ2分析
(2)配对四表格的χ2分析
(3)行列表(R×C)资料
- 双向无序资料的χ2分析(样本率和构成比的比较)
- 单向有序资料(分组变量有序,反应变量无序)的χ2分析
- 单向有序资料(分组变量无序,反应变量有序)的非参数检验
- 双向有序属性不同资料分析
- 双向有序属性相同资料分析
统计量χ2值表示观察值与理论值之间的吻合程度(或者偏离程度),χ2值越大偏离程度越大,χ2值越小吻合度越好。χ2检验的基本思想同方差分析类似,同样是小概率反证法。假设观察频数和理论频数没有差别,在此前提下计算χ2值,借助卡方分布得出获得这个χ2值的概率P。如果概率很小,则假设不成立,其对立面成立的可能性很大。
【1】四表格资料的χ2分析
表格结构
例1.1 拉贝洛尔和硝苯地平治疗妊高症,新生儿不良反应发生率是否有差别?(Hypertension. 2017;70:00-00. DOI: 10.1161/HYPERTENSIONAHA.117.09972.)
| Group | AE | NO AE | 合计 | 发生率(%) |
| labetalol | 11 | 40 | 51 | 21.57 |
| nifedipine | 17 | 35 | 52 | 32.69 |
| 合计 | 28 | 75 | 103 | 27.18 |
例1.2 胞磷胆碱与神经节苷酯治疗脑血管疾病的有效率是否有差别?
| 组别 | 有效 | 无效 | 合计 | 有效率(%) |
| 胞磷胆碱 | 46 | 6 | 52 | 88.46 |
| 神经节苷酯 | 18 | 8 | 26 | 69.23 |
| 合计 | 64 | 14 | 78 | 82.05 |
以例1.1为例,SPSS操作步骤如下:
①变量设置及数据录入:

Values值:分组(Group)赋值1=labetalol,2=nifedipine;不良反应发生例数(nAE)赋值0=未发生,1=发生。
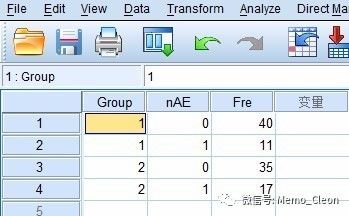
②数据加权:
数据(Data)>>加权个案(Weight Cases),激活加权个案,将频数(本例为Fre)选入频数变量(Frequency Variable)
分类数据的录入往往并非一条记录对应一个样本,而是整理后的频数,因此分析前需要加权告知系统
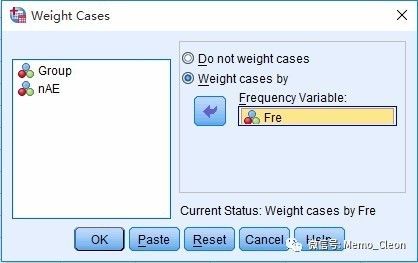
③分析(Analyze)>>描述统计量(Descriptive Statistics)>>交叉表(Crosstabs)
- 行变量(Rows):本例选入Group;
- 列变量(Columns):本例选入nAE
- 统计量(Statistics)…选中卡方(Chi-square)
- 单元格(Cell)…可根据需要选择需要显示的计数、百分比、残差以及组间多重比较的Z检验等。本例选中计数(Counts)中的观察值(Observed)和期望值(Expected)
主要分析结果:
样本量n=103>40,理论频数T(Theoretical frequency,即期望频数expected frequency)均大于5,满足Pearson χ2 的使用条件。
Pearson χ2 =1.609,P=0.205>0.05,妊高症患者在接受拉贝洛尔或硝苯地平降血压治疗后,新生儿不良反应没有统计学差异。
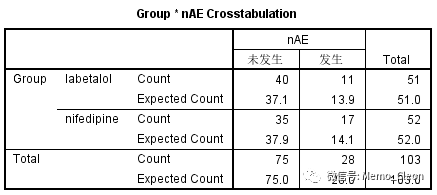
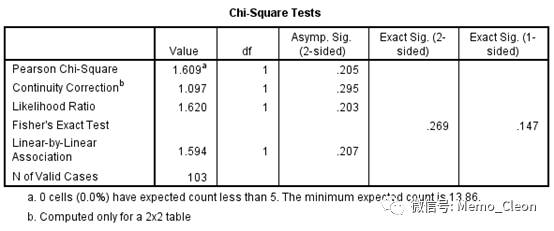
注结果选择
- n≥40 且T≥5:Pearson χ2 (Pearson Chi-square)
- n≥40 且1≤T<5:连续矫正χ2 (Continuity Correction) 或Fisher 确切概率法(Fisher's Exact Test)。连续矫正仅用于四表格。
- n<40,或T<1:Fisher 确切概率法(Fisher's Exact Test)
另外,似然比卡方(Likeihood Ratio)与Pearson χ2 类似,只是采用了不同的计算方法,线性卡方(Linear-by-Linear)用于两变量有无线性相关的检验。
【2】配对四表格的χ2分析
表格结构
175份临床样本接受两种培养基的培养结果
甲培养基 | 乙培养基 | ||
阳性 | 阴性 | 合计 | |
阳性 | 55 | 42 | 97 |
阴性 | 10 | 68 | 78 |
合计 | 65 | 110 | 175 |
普通四表格的行变量和列变量是同一样本的不同属性,如行变量是分组变量而列变量是发生率;配对四表格与普通四表格的不同在于,配对四表格的行变量和列变量是同一样本的同一属性,例如同一种疾病采用不同的诊断方法,行变量是一种方法,列变量是另外一种方法,这时候如果比较两种诊断结果是否有差异,采用的方法就是配对四表格χ2检验(McNemar Test),此类设计的分析的目的往往还要看两种诊断方法的一致程度(吻合程度)如何,这时就需要Kappa一致性检验。
①变量设置及数据录入:变量Medium1表示甲培养基,Values值1=阳性,0=阴性;Medium2表示乙培养基,Values值1=阳性,0=阴性;发生频数用变量Fre表示。

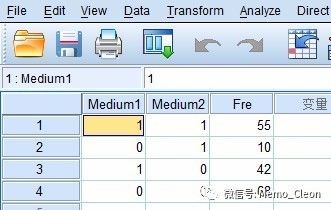
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>描述统计量>>交叉表(Crosstabs)
行变量:本例选入Medium1;列变量:本例选入Medium2
统计量(Statistics)…选中Kappa以及McNemar
单元格(Cell)…选中观察值(Observed)和期望值(Expected)
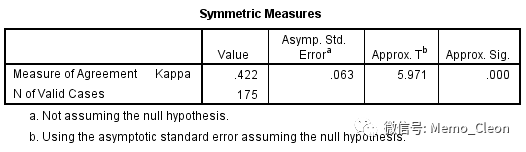
主要分析结果:
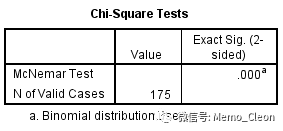
SPSS中并没有对b+c做判断,直接看结果即可(手动计算时,需要根据b+c的结果看是否需要校正,本例b+c=10+42=52>40,无需要校正)。
McNemar卡方结果显示,P<0.001,说明两种培养基的检测结果差异有统计学意义。
Kappa检验的H0假设是两者完全无关,即Kappa=0。本例结果κ=0.422,P<0.001,说明两种培养基的检测结果存在一致性,但一致性一般。【一般根据经验,kappa≥0.75表明一致性较好,0.4≤kappa<0.75一致性一般,kappa<0.4一致性较差】
【注:本例统计学结论“结果有差异,存在一致性”貌似相矛盾,但要仔细区别差异比较和吻合程度检验的不同】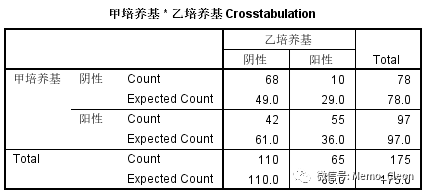
【3】行列表(R×C)资料
3.1 双向无序资料的χ2分析
表格结构:
例3.1.1 样本率比较:三种疗法治疗周围性面神经麻痹的有效率
分组 | 有效 | 无效 | 合计 | 有效率(%) |
物理疗法组 | 199 | 7 | 206 | 96.60 |
药物治疗组 | 164 | 18 | 182 | 90.11 |
外用膏药组 | 118 | 26 | 144 | 81.94 |
合计 | 481 | 51 | 532 | 90.41 |
例3.1.2 构成比差异:2型糖尿病肾病(DN)患者ACE基因型(I/D)分布
组别 | DD | ID | II |
DN组 | 42(37.8) | 48(43.3) | 21(18.9) |
无DN组 | 30(21.7) | 72(52.2) | 36(26.1) |
例3.1.3构成比差异
种族 | MN血型 | ||
M | N | MN | |
黄色人种 | -- | -- | -- |
白色人种 | -- | -- | -- |
棕色人种 | -- | -- | -- |
黑色人种 | -- | -- | -- |
以3.1.1为例,SPSS操作步骤如下:
①变量设置及数据录入:变量Group表示治疗方法,Values值1=物理疗法,2=药物治疗,3=外用膏药;Effect表示治疗效果,Values值1=有效,0=无效;发生频数用变量Fre表示
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>描述统计量>>交叉表(Crosstabs)
行变量:本例选入Effect;列变量:本例选入Group【多重比较要求将分组变量为列变量,见统计量选项】
统计量…选中卡方(Chi-square)
单元格(Cell)…选中计数中的观察值(Observed)、Z检验(Z-test)中的比较列比例(Compare column proportions)和调整P值(Adjust p-values (Bonferroni method))、百分比(Percentages)中的列(Column)
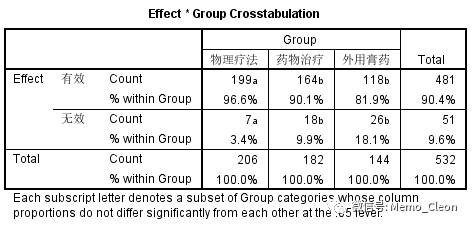
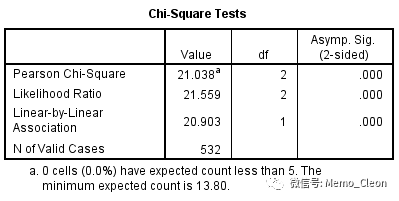
分析结果如下:
χ2 =21.038,P<0.001,可以认为治疗周围性面神经麻痹的的三种疗法的有效率有统计学差异,物理疗法的有效率(96.6%)最高。
需要注意行列表采用Pearson χ2 的条件,要求理论值T>1,且1<T<5的格子数<20%。卡方检验表格下方显示最小期望值(理论值)13.80,小于5的期望值格子数为0(0%),满足Pearson χ2 的条件,如不满足条件则需要采用似然比卡方(Likeihood Ratio)或者增加样本、数据合并来实现。
多重比较结果显示物理疗法的效果要好于药物治疗和外用膏药(P<0.05),而药物治疗和外用膏药的有效率却无统计学差异(P>0.05)。
下标字母相同的列,其比例在0.05 级别上彼此并无显著差异。仔细可能会注意到,在同一组的有效和无效数据的标记相同(即上下两行的标记相同),我们只要知道这是组间标记的作用即可。
两两比较的方法还可以采用χ2 分割法等多种方法。χ2 分割法就是将R×C资料进行多次两两比较,但需要对α值做出校正。
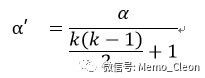
k为样本率的个数。
本例k=3,α按0.05水平计算,校正的α'=0.0125。
①选择比较组
数据>>选择个案:如果条件满足 if……Group=1 | Group = 2
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>描述统计量>>交叉表(Crosstabs)
- 行变量:本例选入Effect
- 列变量:本例选入Group
- 统计量…选中卡方(Chi-square)
分析结果:χ2 =6.756,P=0.009<0.0125,物理疗法与药物治疗有效率差异有统计学意义;
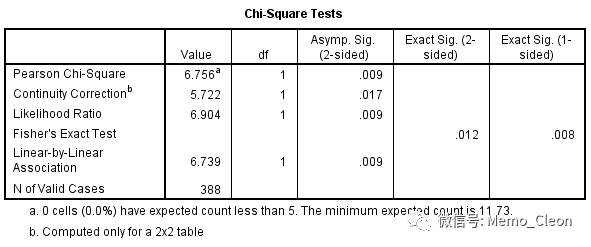
同法可得
物理疗法 VS 外用膏药:χ2 =21.323,P<0.001<0.0125
药物治疗 VS 药物治疗:χ2 =4.591,P=0.032>0.0125
这与Z检验的结果完全一致。
例3.1.2及3.1.3分析同上。
3.2 分组变量有序、反应变量无序资料的χ2分析
表格结构
不同年龄组肺炎患者的不同性质肺炎情况(大叶性肺炎、小叶性肺炎、间质性肺炎)。分组因素年龄为有序变量,但反应变量肺炎种类为无序变量
年龄(岁) | 肺炎性质 | ||
小叶性肺炎 | 大叶性肺炎 | 间质性肺炎 | |
| 0-1 | -- | -- | -- |
| 1-3 | -- | -- | -- |
| 3-7 | -- | -- | -- |
| 7-12 | -- | -- | -- |
| 12-18 | |||
| 18-40 | |||
| 40-60 | |||
| ≥60 | |||
分析方法及操作步骤完全等同于同3.1 双向无序资料的χ2分析
3.3 分组变量无序、反应变量有序资料的非参数检验
表格结构
脱敏治疗联合药物治疗与单独使用药物治疗过敏性鼻炎的疗效对比
| Group | 无效 | 改善 | 显著改善 | 合计 |
| slit+drug | 6 | 19 | 35 | 60 |
| drug | 14 | 20 | 24 | 58 |
| 合计 | 20 | 39 | 59 | 118 |
此种数据结构最大的特点在于反应变量有等级的,“无效-改善-明显改善”明显程度不同,使用Pearson χ2 分析只是对数据结构的差异做出分析,要分析这种等级效应差别Pearson χ2 分析是做不到的,可以使用非参数检验。两独立样本常用Wilcoxon秩和检验和Mann- Whitney U检验。Wilcoxon秩和检验检验统计量为秩和T,当n1≤10和n2-n1≤10时需要查专用T界值表,但当n1>10或n2-n1>10时,可用正态近似法做μ检验(Z检验)。同样Mann- Whitney U检验当样本量较小时(两样本量之和≤30)需要专门的U界值表,样本量大时,可用正态近似法做μ检验(Z检验)。非参数检验的介绍可参见下章笔记,本文只做操作演示:
①变量设置及数据录入:变量Group表示治疗方法,Values值1=slit+drug,2=drug only;Effect表示治疗效果,Values值1=无效,2=改善,3=明显改善;发生频数用变量Fre表示。特别注意“效果”的测量尺度(Measure)属性应该是等级(Ordinal),在使用非参数检验“旧对话框…两独立样本”检验时,不论该属性是等级还是测量尺度(Scale)均可,但在新的对话框中“独立样本”的检测字段中仅允许测量尺度数据,因此在选择统计方法时应注意这个属性。
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>非参数检验(Nonparametric Tests)>>旧对话框(Legacy Dialogs)>>两独立样本(2 Independent Samples)…
检测变量列表(Test Variable List):选入Effect
分组变量(Grouping Variable):选入Group。定义组(Define Group)…组1:1;组2:2
Mann- Whitney U检验分析结果: Z=-2.169,P=0.03<0.05,表明联合治疗效果优于单用药物治疗的效果。
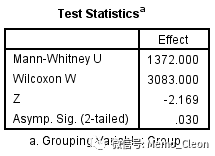
如采用新的对话框,第三步如下
③分析>>非参数检验(Nonparametric Tests)>>独立样本(Independent Samples)…
字段(Field)选项卡:
检测字段(Test Fields):选入Effect
分组变量(Groups):选入Group
新的对话框首先给出的是模型假的结论,P=0.030。双击可看到更为详尽的结果,包括频数图及检验统计量等,结果同旧对话框结果相同。

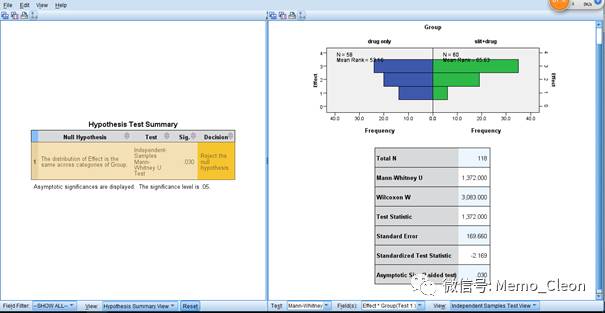
值得注意的是本案如果采用了错误的分析方法,例如采用Pearson χ2,分析结果为χ2=5.244,P=0.073>0.05,两组治疗效果无统计学差异。更有意思的是,如果将示例中“改善”和“显著改善”的例数互换,重新采用Pearson χ2结果跟不换是一样的(χ2=5.244,P=0.073),Pearson χ2仅分析结构,对位置并不敏感。但是例数互换后如采用非参数分析,结果则是Z=-0.731,P=0.465>0.05,与数据互换前完全相反,或许你与真相之间的距离,只差了一个正确的统计学方法。操作步骤从略。
3.4 双向有序属性不同资料分析【行变量和列变量是同一样本的不同属性】
表格结构 年龄与冠状动脉粥样硬化
年龄 | 冠状动脉硬化等级 | |||
- | + | ++ | +++ | |
20- | 70 | 22 | 4 | 2 |
30- | 27 | 24 | 9 | 3 |
40- | 16 | 23 | 13 | 7 |
≥50 | 9 | 20 | 15 | 14 |
此类数据结构应视分析目的的不同而采用相应的分析方法:
3.4.1 不同年龄组患者的冠状动脉硬化等级是否有差别
3.4.2 年龄与冠状动脉硬化是否存在相关性
3.4.3 年龄与冠状动脉粥样硬化等级之间是否存在线性变化趋势
3.4.1 差异比较:采用非参数检验,同反应变量单向有序资料的非参数检验相同,只是示例3.3是两独立样本之间的比较,采用的是Mann- Whitney U检验,而3.4.1是多个独立样本之间的比较,采用的是Kruskal-Wallis H检验。Kruskal-Wallis H检验统计量为H,当样本个数=3和每个样本例数≤5时需要使用H概率分布来查询,当样本个数=3且最小样本例数>5或者样本个数>3时,H近似服从卡方分布。
①变量设置及数据录入:变量Age表示年龄分组,Values值1=20-,2=30-,3=40-,4=≥50;Grade表示动脉硬化等级,Values值0=-,2=改善,1=+,2=++,3=+++;发生频数用变量Fre表示
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>非参数检验>>独立样本(Independent Samples)…
字段选项卡:检测字段选入Grade;分组变量选入Age
分析结果如下:
χ2=66.104,P<0.001,不同年龄组患者的冠状动脉硬化等级差异有差别。双击假设检验模型结果如下。随着年龄的增殖,动脉硬化等级呈增高趋势。当然这种趋势是否是直线趋势,还需要进一步的分析。
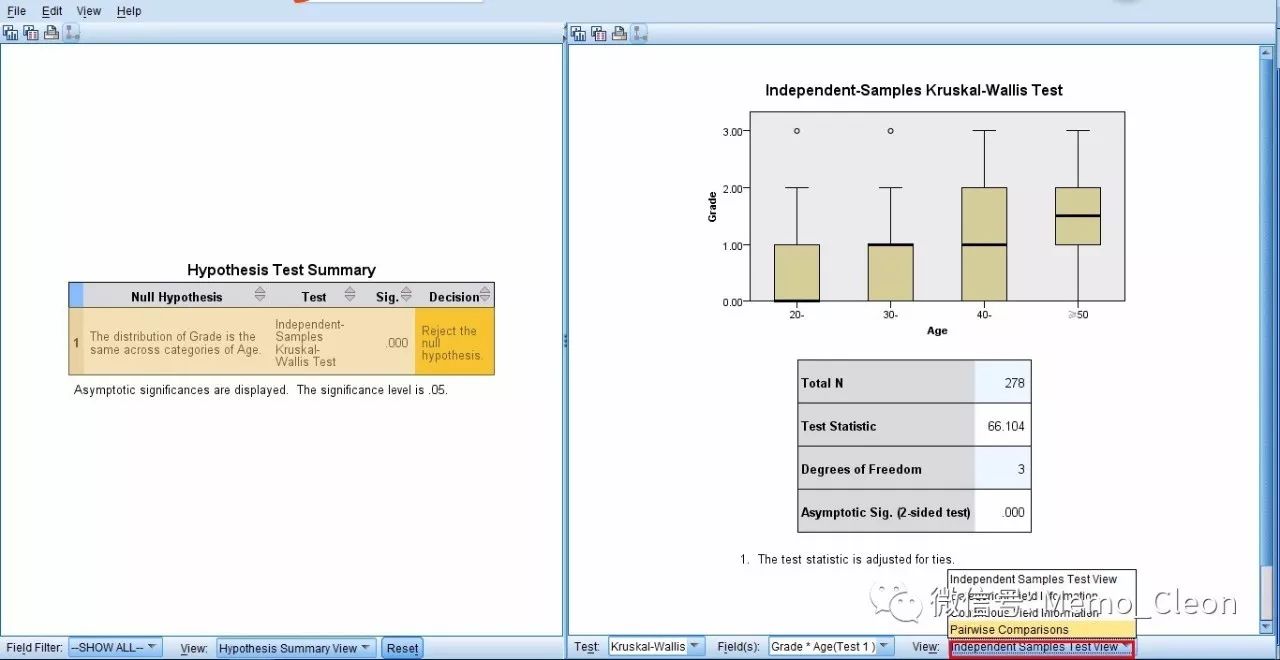
多组比较有统计学差异后如下进一步做两两比较,一般采用Nemenyi test,检验统计量为χ2。可点击右框右下角视图(View)(上图红框)中的成对比较(Pairwise Comparisons)。节点距离的远近反应各组评价秩差异的大小,结果一目了然,不做多的解释。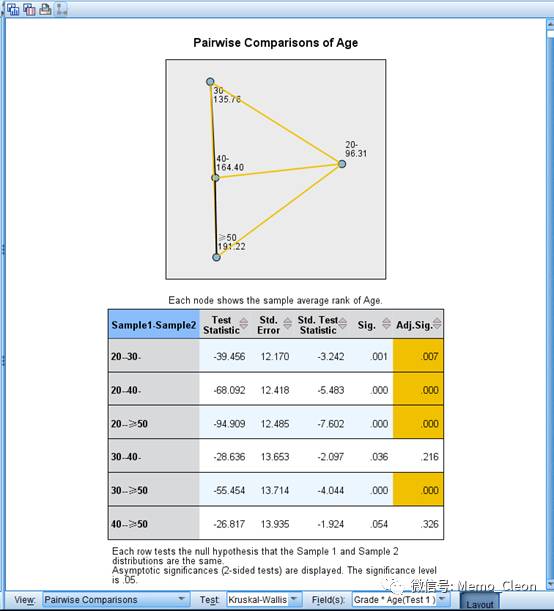
3.4.2 相关性
χ2检验可以定性地检测是否存在相关性,而各种关联指标则可以从定量的角度来说明这种相关性。
变量设置与数据加权同前
③分析>>描述统计量>>交叉表(Crosstabs)
行变量:本例选入Age
列变量:本例选入Grade
统计量…选中Kendall's tau-b等相关指标
注:关联系数一般在0-1或者-1到+1之间,绝对值越大,关联性越强,+-号代表关联方向。
Correlations:相关性,用于两连续变量的分析,结果呈现行、列变量的Pearson相关系数和Spearman等级相关系数。其中Spearman系数和Ordinal中的Kendall's tau-b系数也可以在相关分析(Correlations)的双变量(Bivariate)中得到
Nominal:名义复选框组,有序无序分类均可使用。但两变量均为有序分类时,效率低于“有序复选框组”中的统计量
Ordinal:有序复选框组,两变量均为有序分类
Nominal by Interval:一个名义变量,一个数值变量的关联程度
其他统计量Chi-square(卡方)、Kappa(一致性系数)、Risk(风险系数,计算OR值和RR值)、McNemar(配对检验)以及分层因素存在下的OR值检验方法(Cochran's and Mantel-Haenszel statistics,需要在交叉表对话框中将分层因素选入层(Layer)中)。
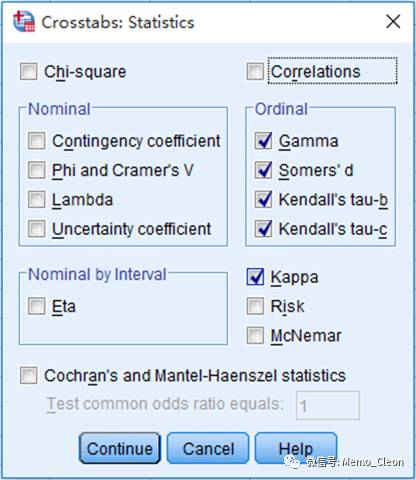
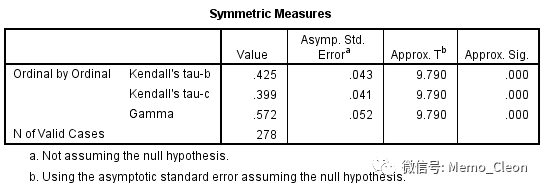
分析结果如下:
年龄与动脉硬化等级存在相关性(P值均小于0.001),但相关系均不高,相关性并不高。
3.4.3 线性趋势
变量设置与数据加权同前
③分析>>描述统计量>>交叉表(Crosstabs)
- 行变量:本例选入Age
- 列变量:本例选入Grade
- 统计量…选中卡方(Chi-square)
分析结果:
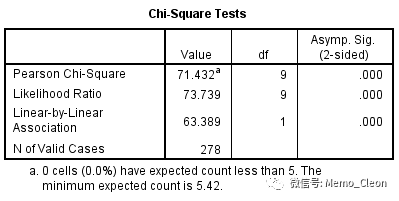
线性卡方(Linear-by-Linear)用于检验行变量和列变量有无线性相关,χ2=63.389,P<0.001,两变量呈直线递增趋势。
注:直线变化趋势检验是将总的χ2值分解为线性回归分量χ2回归和偏回归分量χ2偏。χ2回归和χ2偏均有统计学差异则表明两者存在相关性,但不是简单的线性相关;如果χ2回归有统计学差异而χ2偏无统计学差异则表明两者不仅存在相关性,而且是线性相关。
3.5 双向有序属性相同资料分析【行变量和列变量是同一样本的同一个属性】
表格结构 两种过敏原检测系统检检测结果的比较
中华耳鼻咽喉头颈外科杂志,2010,45( 08 ): 652-655.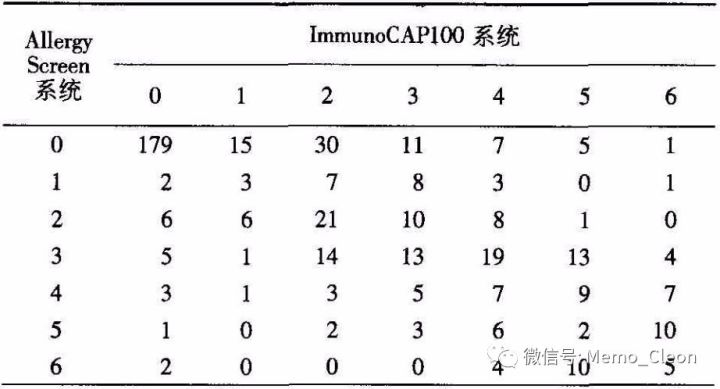
分析目的一般是分析两个变量的吻合性(一致性检验),实际上是配对四表格χ2检验的扩展
SPSS操作步骤
①变量设置及数据录入:变量AllergyScreen表示敏筛系统,Values值0=0级,1=1级,2=2级,3=3级,4=级,5=5级,6=6级,UniCAP表示法玛西亚检测系统,Values值0=0级,1=1级,2=2级,3=3级,4=级,5=5级,6=6级;发生频数用变量Fre表示。
②数据加权:数据>>加权个案,激活加权个案,将本例为Fre选入频数变量
③分析>>描述统计量>>交叉表(Crosstabs)
- 行变量:本例选入AllergyScreen
- 列变量:本例选入UniCAP
- 统计量(Statistics)…选中Kappa、Kendall's tau-b等等级资料指标
分析结果:
两种系统的检测结果存在相关性(Kendall's tau-b及Spearman Correlation均<0.05),检测结果也存在一致性(Kappa=0.295,P<0.001),但Kappa仅为0.295,一致性一般。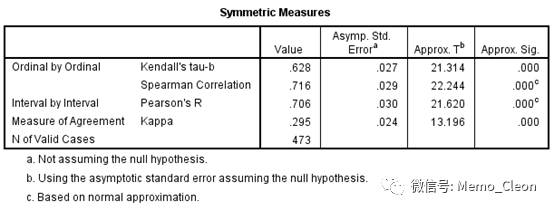
END



来自外部的引用