上次笔记个人对有序logistic回归OR理解为:自变量某取值水平 更倾向因变量低赋值等级效应的可能性 是参照水平的多少倍”,如本笔记后面示例中“男性治疗效果差的可能性女性的3.74倍”。如下表达或许更合适:自变量某取值水平 更可能性倾向因变量的低赋值等级效应 是参照水平的多少倍,比如:男性更可能出现不好的治疗效果是女性的3.74倍。
同时在上一次的笔记中提到不同的统计软件采用的累积logit回归模型有所不同。 SPSS用的是Model 1,而JMP用的是Model 2。*1
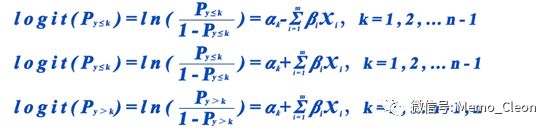

另外自变量的编译方法和参照水平也不同,最终导致模型方程的参数估计值有所差异。When using statistical software, it is important to know: (1) what the default coding method is for categorical variable in regression models and (2) which level is being treated as the reference level. SAS, STATA, SPSS and R, for example, use dummy coding, whereas JMP uses effect coding by default. In SAS and SPSS by default, the last level (of the alphanumeric order) of the categorical variable is considered as the reference level; in STATA and R it is the first level. In JMP by default it is the last level which will be coded -1 for each effect variable.*2。但是转化成相同的表达方式,结果应该是一致的。
JMP操作:示例同因变量有序多分类资料的logistic回归
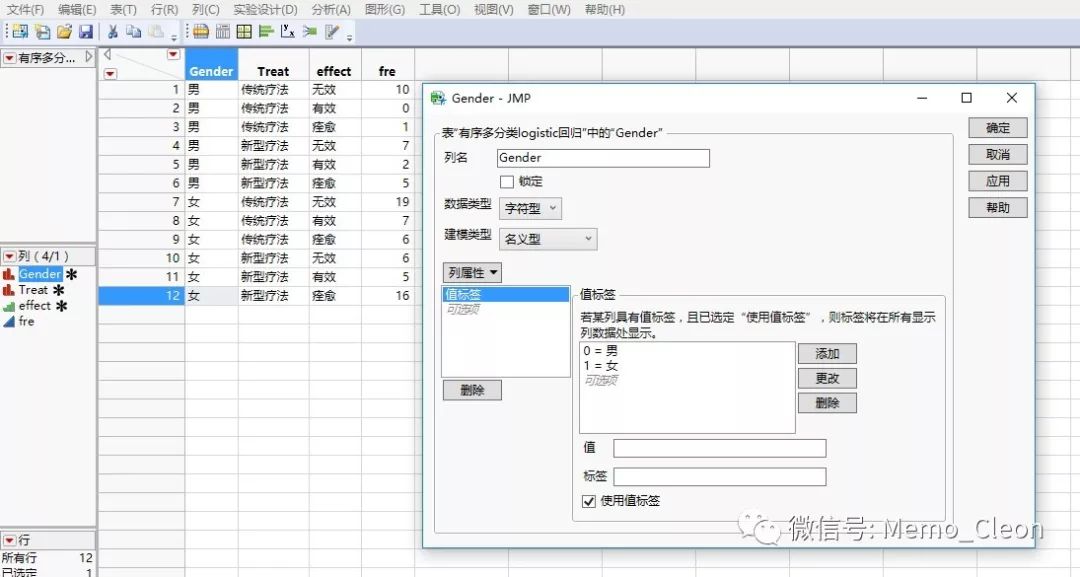
1、数据录入:性别(Gender,数据类型:字符型;建模类型:名义型;列属性>值标签:0=男,1=女);治疗方法(Treat,数据类型:字符型;建模类型:名义型;列属性>值标签:0=传统疗法,1=新型疗法);疗效(effect,数据类型:数值型;建模类型:有序型;列属性>值标签:1=无效,2=有效,3=痊愈);频数(fre,数据类型:数值型;建模类型:连续型)
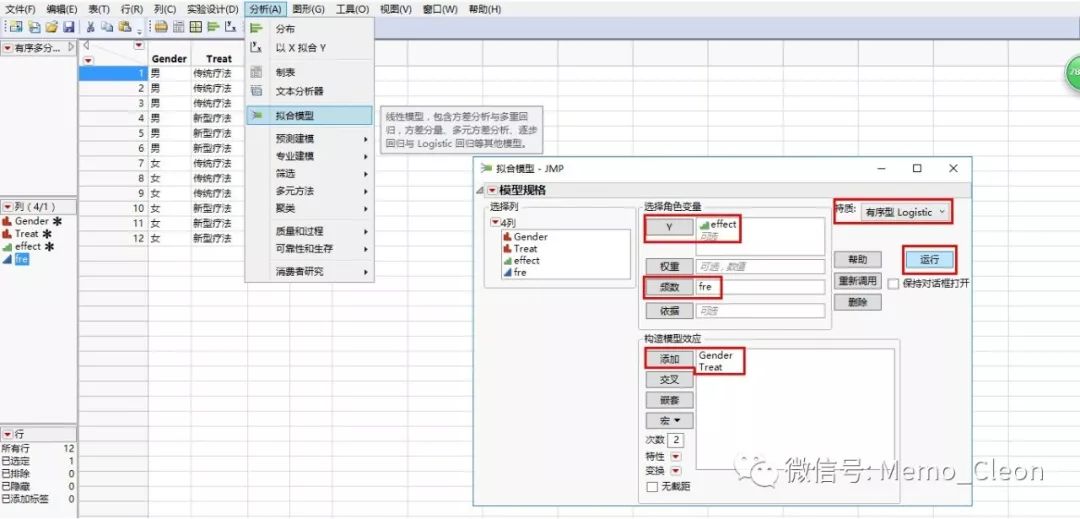
2、有序logistic回归:分析>>拟合模型
【选择角色变量】Y:effect;频数:fre
【构建效应模型】添加:Gender、Treat
【特质】有序型logistic
【运行】
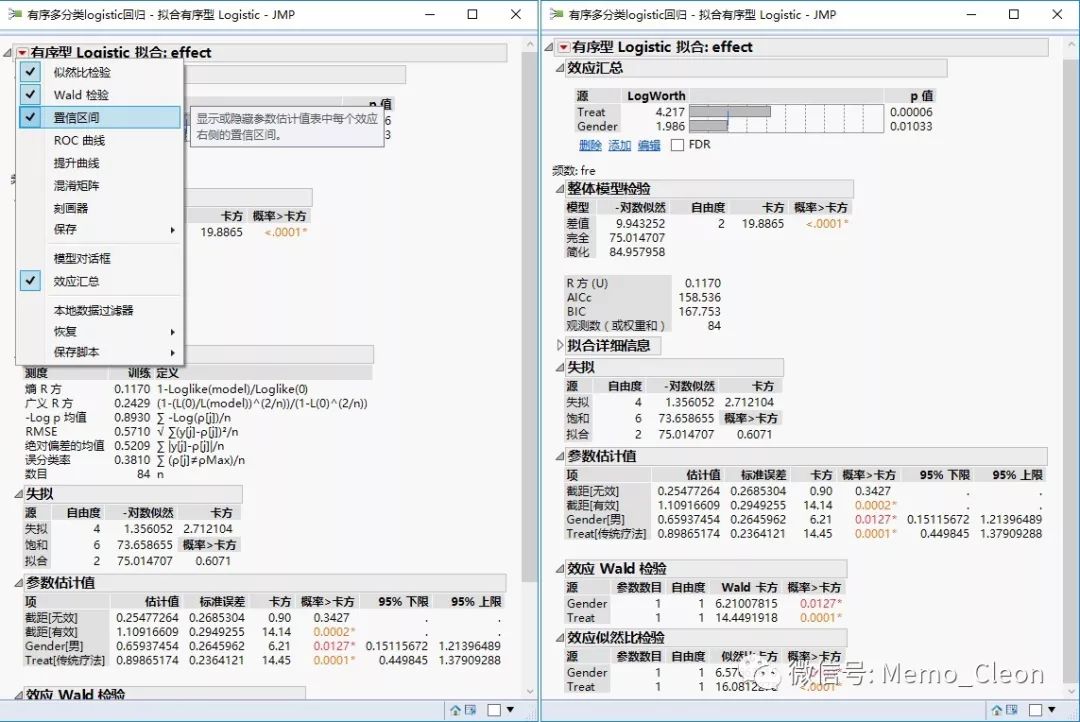
3、结果。 增加wald检验和置信区间。不同于SPSS结果,JMP直接以报表的形式输出所有结果。
增加wald检验和置信区间。不同于SPSS结果,JMP直接以报表的形式输出所有结果。
4、结果解读*3
【1】效应汇总
源列出按 p 值升序排序的模型效应;
logWorth显示每个模型效应的LogWorth,该值定义为-log10(p值)。该变换调整p值以提供适用于绘图的尺度。超过2的值在0.01水平下显著(-log10(0.01)=2)。选中FDR复选框可将logWorth列替换为FDR logWorth列;
条形图显示logWorth(或 FDR logWorth)值的条形图。该图在整数值处标绘垂直虚线,在值2处标绘一条蓝色参考线。
P值显示每个模型效应的p值。这通常是模型结果的“效应检验”表或“效应似然比检验”表中显示的显著性检验所对应的p值。本例显示治疗方案和性别均有统计学意义。
【2】整体模型检验:指定模型是否显著好于简化模型(只含截距的模型),卡方统计量是拟合模型与仅包含截距的简化模型的负对数似然差值的两倍。仅包含截距的 –对数似然值84.96,完整模型减小到75.01,这个减小导致整体模型的似然比卡方统计量为9.94(自由度为2)。χ2=19.887,P<0.001,说明至少有一个自变量的偏回归系数不为0。
另外本部分结果还给出了R方、校正的 Akaike 信息准则 (AICc) 和 Bayesian 信息准则 (BIC) 。R方(U)即SPSS结果中的McFadden的伪R2。较小的AICc和BIC值表示拟合效果更好。
【3】拟合详细信息:对于熵R方和广义R方,值越接近1表示拟合效果越好。对于-log p均值、RMSE、绝对偏差的均值和误分类率,值越小表示拟合效果越好。
熵R方:等价R方(U);
广义R:方亦称为 Nagelkerke或Craig和Uhler R2,可参见SPSS结果;
-log p:均值-log(p) 的平均值,其中 p 是与发生的事件关联的拟合概率;
RMSE:均方根误差,其中差值为响应和 p (实际发生事件的拟合概率)之间的差值;
绝对偏差的均值:响应和p(实际发生事件的拟合概率)的差值绝对值的平均值;
误分类率:具有最高拟合概率的响应类别不是观测到的类别的比率。
【4】失拟检验:即拟合优度检验,饱和模型是否显著好于指定的模型。P=0.607>0.05,拟合优度较好。
【5】参数估计值。这是结果中最重要的部分,给出了截距和回顾系数、标准误、wald卡方检验及票%CI。最终获得两个模型回归方程如下:
logit(Py≤1)=ln(Py≤1/(1- Py≤1))
= 0.255+0.659*Gender+0.899*Treat
logit(Py≤2)=ln(Py≤2/(1- Py≤2))
= 1.109+0.659*Gender+0.899*Treat
这个与SPSS的结果明显不同,SPSS结果如下
logit(Py≤1)=ln(Py≤1/(1- Py≤1))
=-1.303+1.319·Gender+1.797·Treat
logit(Py≤2)=ln(Py≤2/(1- Py≤2))
=-0.449+1.319·Gender+1.797·Treat
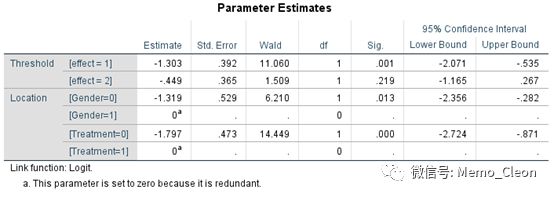
同样的数据,都是使用的有序多分类logistic回归,结果却不同,这个怎么破?让我们通过最基本的数学公式来推导一下这个问题。
SPSS的模型中回归方程的截距是自变量参照水平的均值。自变量采用的是哑变量编译(dummy coding)方式,当自变量为二分类时,两个变量的赋值分别是0和1。以性别为例,截距实际上就是固定自变量treatment,当Gender=0(男)时logit(P)值,即截距是参照组的logit(P)值。当Gender=1(女)时,logit(P)=截距+β。
Y1=logit(Px=0)=ln(Odds0)=α+βX(X=0)即ln(Odds0)=α
Y2= logit(Px=1)= ln(Odds1)=α+βX(X=1)即ln(Odds1)=α+β
∴ln(Odd0)-ln(Odd1)= α-(α+β)=-β 即ln(Odd0/Odd1)=-β 即lnOR=-β
∴OR=exp(-β)
JMP模型中回归方程的截距是自变量各水平均数的均值。自变量采用的是效果编译(effect coding)方式,当自变量为二分类时,第一个(Gender=0)和第二个水平(Gender=1)分别编码为1和-1。
Y1=logit(Px=1)=ln(Odds1)=α+βX(X=1),即ln(Odds1)=α+β
Y2= logit(Px=-1)= ln(Odds-1)=α+βX(X=-1),即ln(Odds-1)=α-β
∴ln(Odds1)-ln(Odds-1)=(α+β)-(α-β)=2β,即ln(Odd1/Odd-1)=2β,即lnOR=2β
∴OR=exp(2β)
性别:①wald χ2=6.210,P=0.013<0.05,说明性别对疗效的影响有统计学差异;②估计值(回归系数β)为正,说明相比女性(自变量高水平,效果编译为-1),男性(自变量低水平)对倾向无效(低赋值等级效应)的影响更大(可以更通俗地表达为相比女性,男性的治疗效果更差)。注意这个跟SPSS相反;③相比女性(自变量高水平,效果编译为-1),男性(自变量低水平,效果编译为1),对倾向无效(因变量低赋值等级效应)的OR值为exp(2*0.6593)=3.74,即男性更可能出现不好的治疗效果是女性的3.74倍。同样的,我们习惯于表达A是B的几分之一或者是几倍,当系数为负值时,我们可能需要结果的倒数,以关注最后一个响应水平而非第一个响应水平。
治疗方案:①wald χ2=14.45,P<0.001,说明治疗对疗效的影响有统计学差异;②估计值为正,说明相比新型疗法,传统疗法的效果更差;③传统疗法更可能出现效果不好是新型疗法的exp(2*0.8987)=6.03倍。
Cornell University Statistical Consulting Unite的“Ordinal Logistic Regression Models and Statistical Software:What You Need to Know”一文中对不同的统计软件采用不同的模型以及回归系数的解释做了详细地、容易理解的介绍*1。
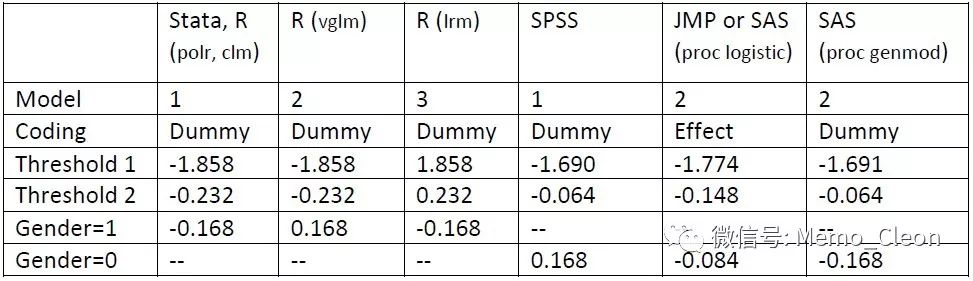
但其认为“However, for SAS proc genmod we would say that women are 0.84 times as likely as men to rate the mattress at a higher score, exp(𝛽1) = exp(-0.168) = 0.84. Note this is the same interpretation as above because the frame of reference changes from women to men and 0.84 = 1/1.18.”个人以为不妥。exp(-0.168)=0.845,而不是等于表中的-0.084,两者相差将近10倍,作者可能看错了。更合适的解释应该是“男性是女性更可能评估床垫低分(不舒服)的exp(2*0.084)倍,即1.18倍”【mattress on a scale from 1 to 3; 1 for uncomfortable, 2 for comfortable, 3 for very comfortable. The categorical explanatory variable of interest is the gender of the respondent; 0 for female, 1 for male】
【6】效应wald检验:回归系数的Wald卡方检验,结果同参数估计值。
【7】效应似然比检验。指定的模型是否显著好于不含给定效应的模型,同效应汇总。与不包含Gender和Treat的模型相比,最终模型均有统计学意义,说明含有Gender和Treat的最终模型拟合效果更好。
*1:Ordinal Logistic Regression Models and Statistical Software:What You Need to Know.
*2:Coding Categorical Variables in Regression Models:Dummy and Effect Coding.
*3:JMP:Fitting Linear Models.Second Edition.
END


