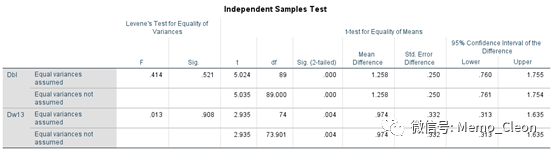
在进行数据分析时,有时候我们会遇到数据基线不平的情况,比如两样本的t检验的示例,比较Labe和Meto用药13周的降压效果,但一开始用药的时候两组舒张压的差别便有统计学意义。除了文中使用的差值比较,协方差分析是一个非常不错的选择。
协变量是对观察结果有影响但无法或难以控制的因素。协方差分析是通过直线回归的方式把协变量值化为相等(协变量取值其总均数)后求得因变量的修正均数,以此控制混杂因素的影响后,用方差分析比较修正均值间的差别。
适用条件:
(1)协变量为连续变量,且各组因变量与协变量呈线性关系;
(2)各组因变量残差呈正态分布;
(3)各组因变量残差等方差;
(4)各组因变量和协变量的回归线平行,即斜率相等。也就是要求对于不同的自变量,协变量对因变量的影响相同。如不满足平行线假定,说明自变量和协变量存在交互作用,他们会同时对因变量产生影响,这样混杂起来我们就无法控制协变量。
(5)在考察因变量与协变量的线性关系时,严格来讲也需要考察建立每条回归直线的前提:线性趋势、独立、正态、方差齐、不存在多重共线、无明显异常点等,具体可参考“多因素线性回归”。
示例“两独立样本的t检验”数据来自excel的自动生成,没有任何实际意义。严格来说,本例因变量与协变量的线性关系也不明显,并不适合使用协方差分析。本例为演示操作步骤和结果解读使用。
示例1 SPSS操作步骤与结果解读
【1】条件考察
(1)因变量与协变量的线性关系考察
Graphs>>ChartBuilder…
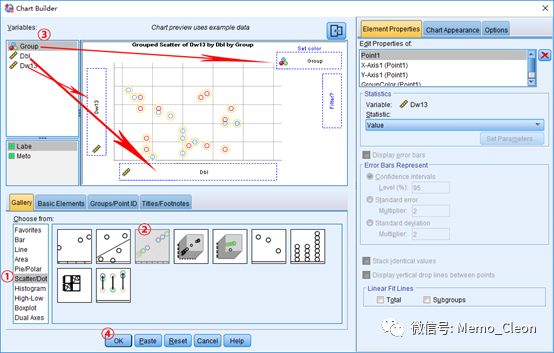
结果显示,不论Labe组还是Meto组,舒张压的基线值与治疗后结果线性关系并不明显,不适合使用线性模型来统计推断。注:本示例数据是通过Excel自动生成,没有任何实际意义。
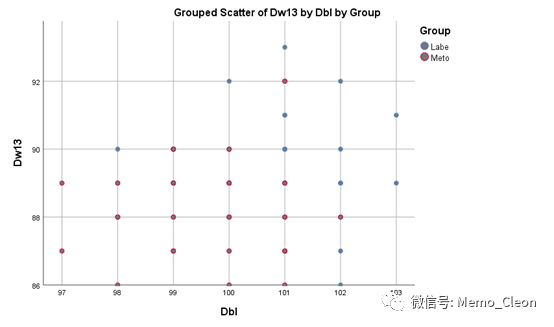
实际上使用线性模型进行拟合的结果也显示,两组的基线值与治疗后的舒张压并不成线性关系,线性拟合步骤如下:
Analyze>>Regression>>Linear…
Dependent(因变量):Dw13;
Independent(自变量):Dbl;变量筛选方法(Method):Enter
SelectionVariables(筛选变量):通过Rule筛选Group=1和Grou=2,分别进行两次线性拟合
主要结果:
Group=1:模型F=0.250,P=0.620;Dbl系数估计值-0.109,t=-0.500,P=0.620。
Group=2:模型F=0.190,P=0.666;Dbl系数估计值0.081,t=0.435,P=0.666。两个模型均只有一个自变量,系数检验和模型检验是一致的。
线性关系不成立是不能直接进行协方差分析的。为更好的演示操作,本例继续协方差进行分析的后续步骤。
(2)平行线假定检验:要检验治疗前和治疗后的舒张压的回归线是否平行,即治疗前舒张压对治疗后舒张压的影响在labe和meto两个组中是否相同,可用治疗前舒张压(Dbl)与治疗方法(Group)是否存在交互作用来表示。
Analyze>>GeneralLinear Model>>Univariate…
因变量:Dw13;固定因素:Group;协变量:Dbl
Model…对话框>>选择“Build Term”构建含有“Group、Dbl、Group*Dbl”的模型
其他默认选项
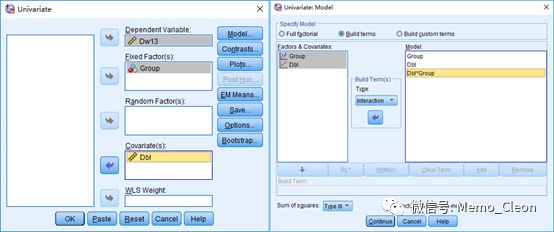
注:Model…对话框:全因素模型可以考察所有因素及其之间的交互作用,但各因素与协变量的交互作用不会输出,需要强行纳入处理因素和协变量的交互作用以进行分析,即group处于不同水平时,Dw13随Dbl变化的斜率是否相等。
结果显示:Group与Dbl的交互项无统计学意义(F=0.442,P=0.508),可以认为两组的斜率相同。
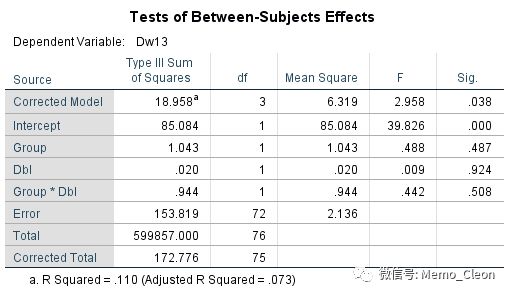
(3)残差正态性与方差齐性考察
生成残差:Analyze>>General Linear Model>>Univariate…
因变量:Dw13;固定因素:Group;协变量:Dbl。
Save…对话框>>PredictedValues:Unstandardized;Residuals:Unstandardized、Srandardized。
正态性与方差齐性考察:Analyze>>Descriptive Statistics >>Explore…
因变量列表选入新生成的变量“Residual for Dw13[RES_1]”,因素列表选入“Group”;
Plots…对话框>>选中Normality plots with tests、Spread vs Levelwith Levene Test中的Untransform。方差齐性检验也可以直接在“选项”对话框中选择“Homogeneity tests”。
结果显示:Labe组数据呈正态,Meto组数据正态性一般,结合QQ图可以认为近似正态。可以认为两组方差相等。
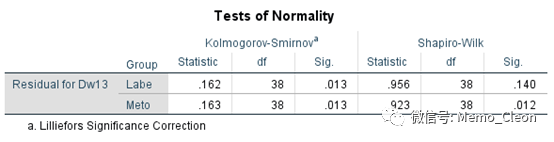
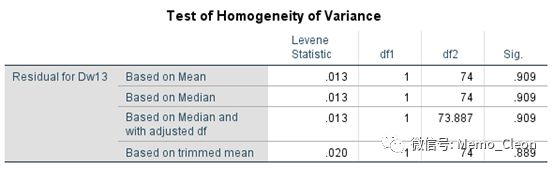
正态性和方差齐性的检验方法很多,具体可参考正态分布与方差齐性的检验方法与SPSS操作,若要求不严格,可以直接用原始数据代替残差进行检验。
(4)因变量与协变量的线性回归条件检验本例略,可参考“多因素线性回归”。
【2】协方差分析
Analyze>>GeneralLinear Model>>Univariate…
因变量:Dw13;固定因素:Group;协变量:Dbl。
Model(模型)…>>选择“Build Term”构建含有“Group、Dbl”的模型。或者直接选择默认的全因素(Full factorial)模型。在适用条件的分析中,已经得出两组斜率相同,Group和Dbl的交互项无统计学意义,因此Group*Dbl应从模型中剔除。
EMMeans(边际均数)…>>显示边际均值框选入Group。选中“比较主效应”用于所选因素不同水平的主效应的边际均值两两比较,默认LSD法,本例只有两组,跟组间整体比较是一致的。“边际均数”的各个选项在旧版本中存在于“选项”对话框中。边际均数是剔除了其他变量的影响用于各水平比较的估计值,当分析模型含有协变量,边际均值和原始均值并不对应。
Save(保存)…>>去掉在平行性检验中选中的变量。
Options(选项)…>>Display(输出内容):Descriptive statistics(描述性统计量)、Parameterestimates(参数估计)、Homogeneity tests(方差齐性检验)。
其他默认选项。
【3】结果与解读
(1)受试者间因素信息

(2)描述性统计量。两组舒张压在用药13周后绝对数值上有差异。
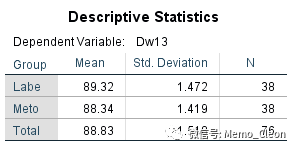
(3)方差齐性检验:可以认为两组残差方差齐同(F=0.013,P=0.909>0.05)。

(4)受试者间效应检验。考虑了协变量之后的方差分析结果。舒张压的基线水平对治疗结束的舒张压没有影响(F=0.000,P=0.985>0.05),不同的用药方案治疗结束后舒张压不同(F=6.599,P=0.012<0.05)。
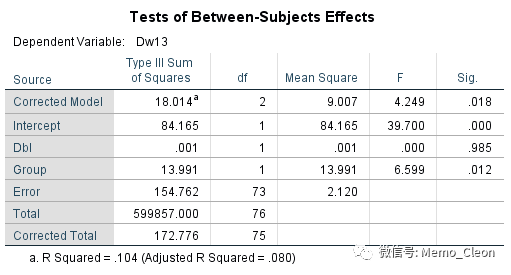
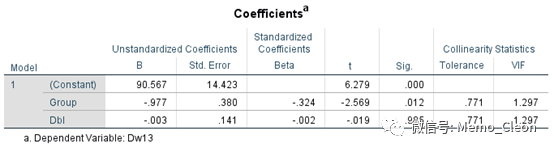
(5)参数估计。给出模型方程的一些系数,Dw13=88.613-0.003Dbl+0.977Group。注意SPSS默认以取值较高的水平(Group=2)为对照。舒张压的基线水平对治疗结束的舒张压水平没有影响(t=-0.109,P=0.985>0.05),与Meto组相比,Labe组治疗后血压值偏高0.977(t=2.569,P=0.012<0.05)。
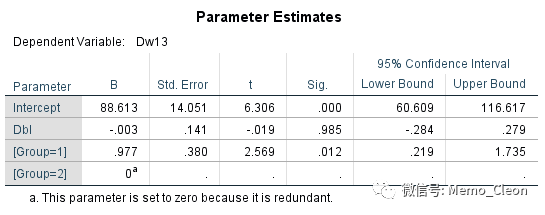
(6.1)修正均值估计。一般来说经过修正后组间差异会变小,原数据均值可参见描述性统计量表的结果。另外表格还显示,Dw13的修正均值是按基线Dbl=100.2进行评估,这个值实际上就是协变量的总均数。
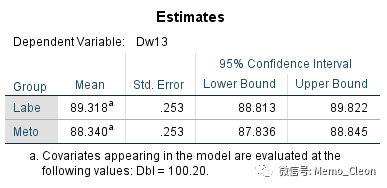
(6.2)修正均值成对比较。本例只有两组,与6.3的整体比较结果一致。
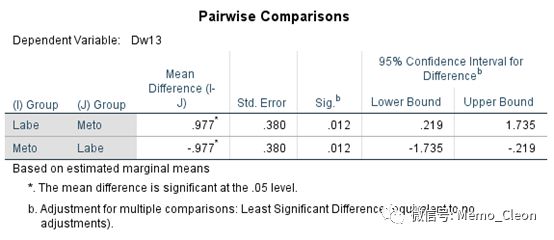
(6.3)修正均值的单因素方差分析。组间效应的方差分析结果,同受试者间效应检验结果一致。不同的用药方案治疗结束后舒张压不同(F=6.599,P=0.012<0.05)。
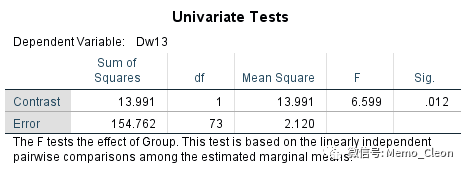
【4】多重线性回归也可以用于这种协变量的分析。
Analyze>>Regression>>Linear…
Dependent(因变量):Dw13;
Independent(自变量):Dbl、Group;变量筛选方法(Method):Enter。
主要结果与协方差分析的参数估计一致,系数检验也与协方差分析的组间t检验结果完全一致,不再累述。系数表中Group的系数为-0.977,而协方差分析中为0.977,是参照水平不同造成的。
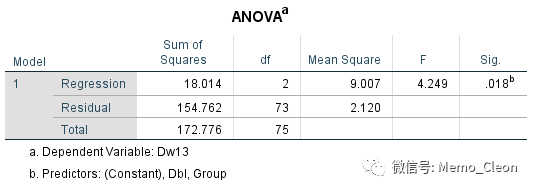
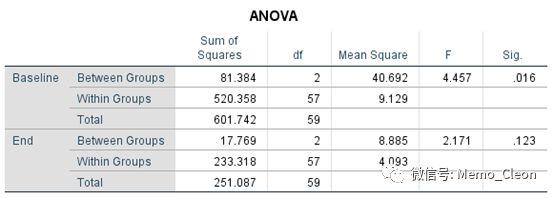
示例2 :60名糖尿病患者随机分为3组,分别给与常规药、新药A和新药B的降血糖治疗,比较3组治疗的血糖值。
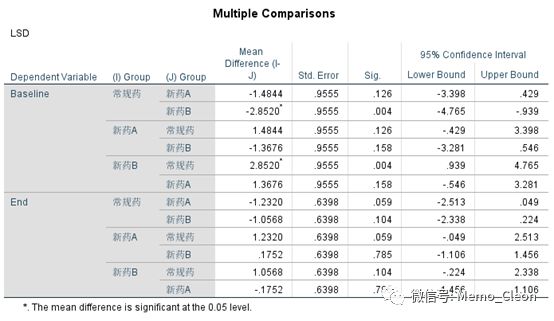
这个案例,第一考虑就是采用完全随机设计的方差分析,可以直接使用One-Way ANOVA过程或者Univariate过程进行,具体过程可参考方差分析。结果显示,3组治疗后效果没有统计学差异(F=2.171,P=0.123)。但同时我们也发现治疗前的血糖的基线值有统计学意义(F=4.457,P=0.016<0.05),其中常规药和新药B存在统计学差异(P=0.004)。我们很难说治疗后的效果没有统计学差异,是因为不同的给药方法治疗效果一样,还是因为基线值的差异造成的。可以考虑使用协方差分析剔除基线值对结果的影响。
【1】条件考察。
(1)线性趋势考察:Graphs>>Chart Builder…
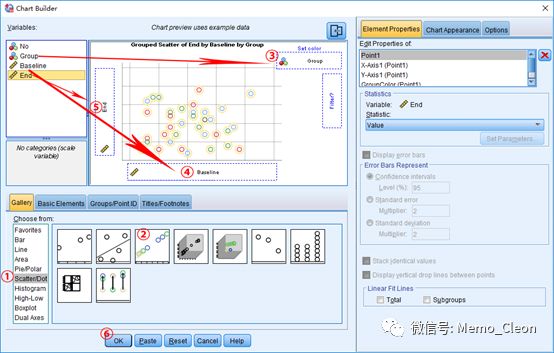
结果显示3组线性趋势较为明显。但从拟合线上看,3条回归直线存在交叉,可能不满足回归线平行的条件,需要在统计学上进行检验。
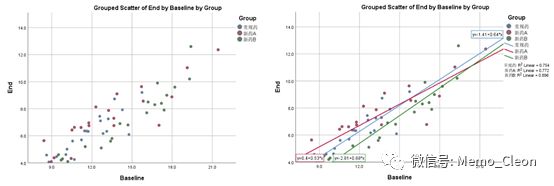
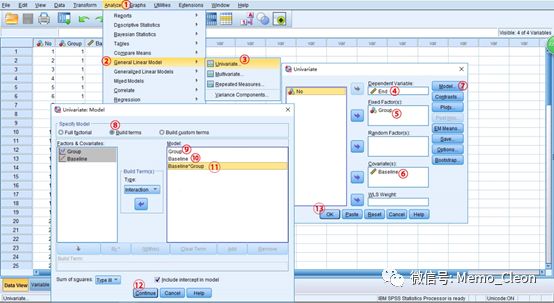
(2)平行线检验:Analyze>>General Linear Model>>Univariate…
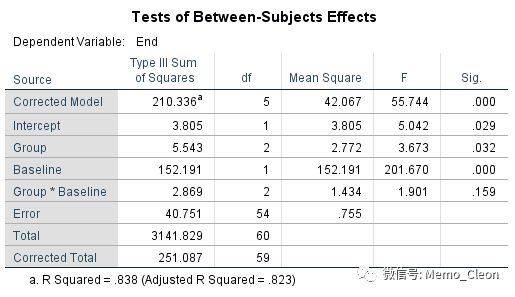
结果显示协变量与分组变量交互作用没有统计学意义(F=1.901,P=0.159>0.05),满足回归线平行的条件。
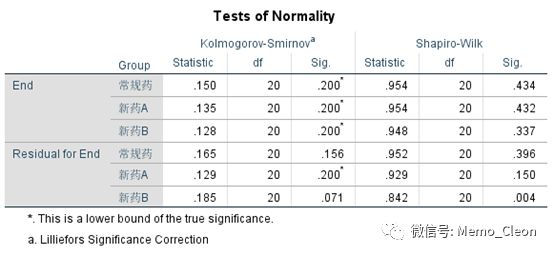
(3)正态性、方差齐性考察。步骤略,可参见示例1。各组数据残差呈正态分布,方差齐同。
【2】协方差分析:Analyze>>General Linear Model>>Univariate…
主要结果:
(1)受试者间因素信息。
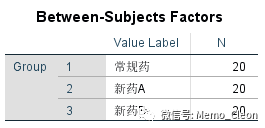
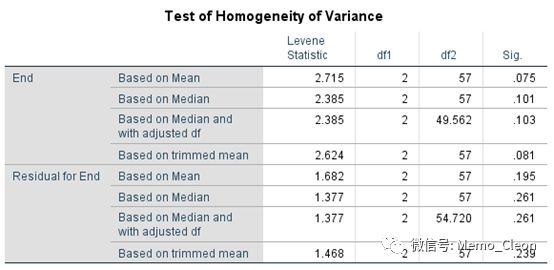
(2)描述性统计量。三组血糖值在用药后平均值、标准差及案例数。
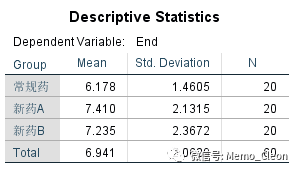
(3)方差齐性检验:三组残差方差齐同(F=1.682,P=0.195>0.05)。

(4)受试者间效应检验。建立的分析模型有统计学意义(F=88.784,P<0.001),说明至少有一个因素(分组变量或协变量)对因变量有影响。基线值(协变量值)的确能对最终的结果产生影响(F=243.549,P<0.001),不同的用药方案治疗效果也不同(F=6.299,P=0.003<0.001)。
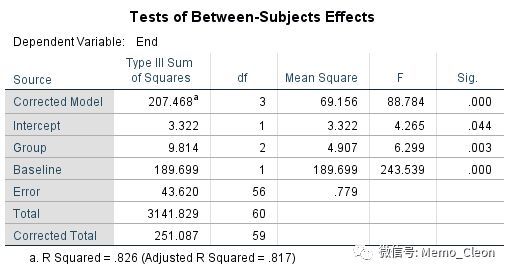
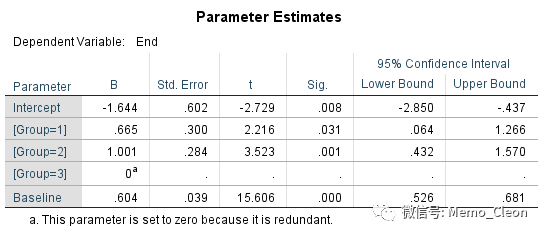
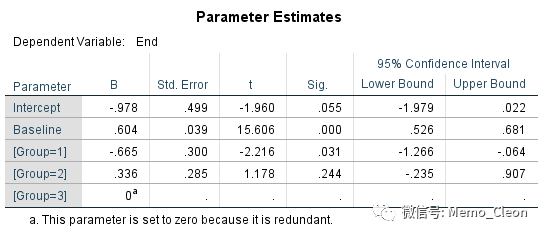
(5)模型参数估计。基线值(协变量值)对最终结果的影响有统计学意义(t=15.606, P<0.001),t值15.606=协方差分析中F值243.549的平方,治疗前血糖每升高1mmol/L,治疗后血糖升高0.604mmol/L。与药物B(Group=3)相比,常规药物(Group=1)有治疗效果更差(t=2.216,P=0.031<0.05),将药物B改用常规药物进行治疗,血糖升高0.665mmpl/L;与药物B(Group=3)相比,药物A(Group=2)有治疗效果更差(t=3.523,P=0.001<0.05),将药物B改用药物A进行治疗,血糖升高1.001mmpl/L。
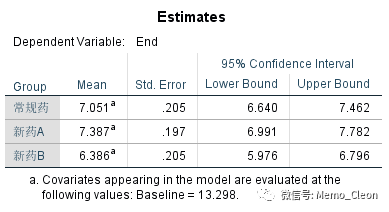
(6)边际均数的估计值。因变量边际均数、标准误及95%置信区间,治疗后血糖值End的修正均值是按基线Baseline=13.298进行评估,该值是协变量基线值的的总均数。
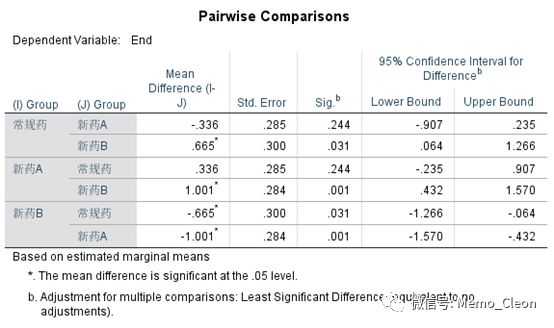
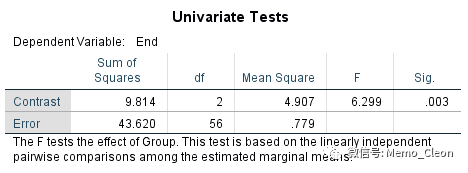
(7)边际均数的成对比较。结果显示药物B治疗效果好于常规药物(P=0.031)和药物A(P=0.001),药物A和常规药物治疗效果没有统计学差异(P=0.244)。边际均数是剔除了其他变量的影响用于各个水平比较的估计值,当分析模型含有协变量,边际均值和原始均值并不对应,原始均值的Post Hoc比较可参见示例2开始处表格。
(8)受试者间边际均数的总体比较。同受试者间效应检验结果一致,F=6.299,P=0.003,不同的用药方案治疗效果也不同。
【3】同样的,该示例也可改用多因素线性回归,可以得到与协方差分析相一致的结果,但需要对无序多分类的分组变量(Group)进行哑变量设置,以常规药物(Group=1)为参考水平为例,步骤如下:
(1)DrugA哑变量编码:Transform>>Recodeinto Different Variables…
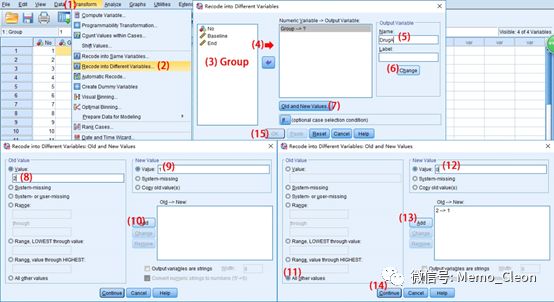
重复以上操作(或在DrugA哑变量设置基础上对Old and New Variable对话框中的赋值修改),进行DrugB的哑变量编码。如果变量较多,可以直接在完成第一个哑变量的编码后,点击Paste按键进入程序编辑器,复制黏贴修改赋值的方法进行全部哑变量的设置,如本例可以复制第一行,然后对赋值进行修改,如下(黑体为粘贴修改后的内容):
RECODE Group (2=1) (ELSE=0) INTO DrugA.
RECODE Group(3=1) (ELSE=0) INTO DrugB.
EXECUTE.
然后点击运行即可。
(2)多因素线性回归:Analyze>>Regression>>Linear…
Dependent(因变量):End;
Independent(自变量):Baseline、DrugA、DrugB;变量筛选方法(Method):Enter。要特别注意,哑变量要遵循同进同出的原则,如进行变量筛选,可以将哑变量放在一个Block中进行。
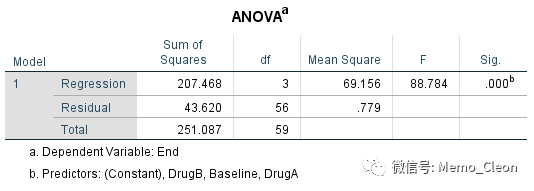
(3)主要结果:回归模型有统计学意义(F=88.784,P<0.001),基线值(协变量值)的确能对最终的结果产生影响(t=15.606, P<0.001), t值15.606=协方差分析中F值243.549的平方,治疗前血糖每升高1mmol/L,治疗后血糖升高0.604mmol/L。与常规药物相比,药物B具有更好的治疗效果(t=-2.216,P=0.031<0.05),将常规药物改用药物B进行治疗,血糖可以降低0.665mmpl/L,而药物A的治疗和常规药物的治疗效果类似(t=1.178,P=0.244>0.05)。
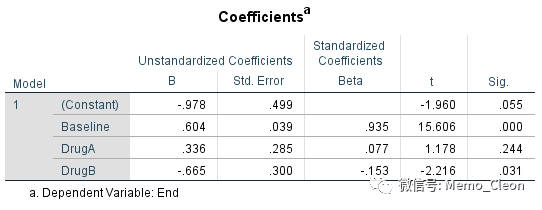
注意示例编码是DrugA和DrugB是与常规药物相比,如要比较药物A和药物B则需要对哑变量的赋值进行修改。此处有人可能会发现,系数与协方差分析的参数估计系数估计值不一致,这是因为SPSS默认以取值较高的水平(Group=3,DrugB)为对照,如将常规药、药物A和药物B分别赋值为3、2、1,并在数据表中对应的记录做修改后做协方差分析,结果和采用哑变量的分析完全一致,结果如下:
还有一个问题要考虑,当协变量与因变量的回归线不平行,及分析因素与协变量存在交互作用时,该如何处理?除了数据变换处理,可以进行分段进行协方差分析,或者在分析因素不同水平上分别进行分析。在多因素线性回归中,我们可以考虑引入交互项,但引入交互项和可能带来的问题是分析因素与交互项存在多重共线,在多因素线性回归一文的最后,我们采用的方法是将变量中心化。当然也可以不引入交互项,而在分析因素不同水平上分别进行线性回归。最后,本例拟合多因素线性回归将无序多分类的分组因素重新编码为哑变量,对分类变量除了使用这种办法,还可以使用分类变量的最优尺度回归来进行。


