利血平可以使小鼠的去甲肾上腺素等递质下降,现考察某种新药是否具有对抗利血平的降递质作用,将24只小鼠随机分为4组,并给与不同的处理后,测量闹钟去甲肾上腺素的含量(ng/g组织),结果如下:
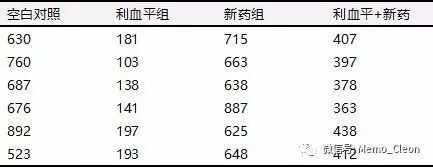
试进行分析利血平和此新药是否均有递质下降的作用?两者是否有交互作用?
从数据结构上看,这种数据似乎可以直接使用单因素的方差分析,一个因素4个水平:
(1)正态性与方差齐性检验:各组呈正态分布,方差齐同。具体操作略。
(2)单因素方差分析:Analyze>>Compare Means>>One-Way ANOVA…
因变量列表:NA(脑神经递质含量);因素:Group(4个水平,1:空白对照;2利血平组;3:新药组;4:利血平+新药组)。
PostHoc…对话框:选择LSD。
(3)结果:4组间有显著的统计学差异(F=59.306,P<0.001)。两两比较结果显示:与空白对照组相比,新药组并没有显著降低神经递质的含量,但其他任意两组间差异均有统计学意义。
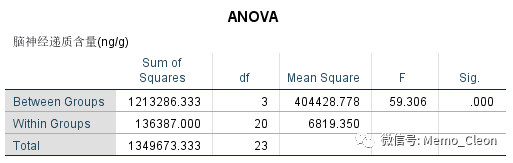
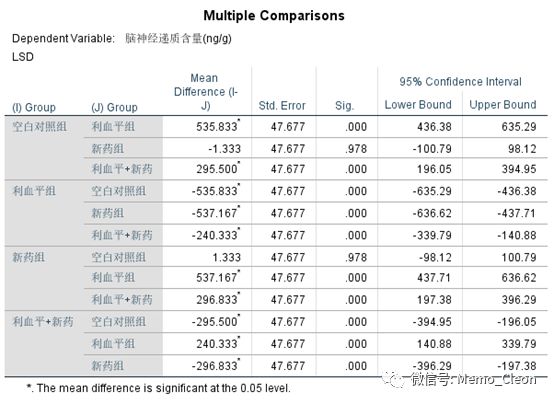
单因素分析One-Way ANOVA过程的主要结果止步于此了,但研究者还想看一下新药和利血平之间是否有交互作用,单因素方差分析就无能为力了。实际上这是一个典型的析因设计(Factorial Design)。析因设计可以对影响因素进行全面的分析,比如各因素的效应,也可以研究各因素之间的交互作用并寻找不同因素各水平间的最佳组合。但需要特别注意,当存在交互作用时,主效应不能反应因素的作用,需要计算某个因素在另个一个因素不同水平上的单独效应。
析因设计的方差分析适用条件:独立、正态、方差齐。
析因设计的方差分析可将总变异分解为:处理组间效应和误差,其中处理组间效应又包括每个因素的主效应、各因素的交互作用。以两因素为例,析因设计模型:Yijk=μ+αi+βj+(αβ)ij+εijk。Yijk表示在A因素i水平和B因素j水平作用下第k位个体的具体值,μ表示总平均水平,αi表示A因素i水平的附加效应(A因素i水平比平均水平的改变量),βj表示B因素j水平的附件效应,(αβ)ij表示A因素i水平与B因素j水平时两者的交互作用,ε随机误差,假定其服从正态分布。各名词概念可参见文末解释。
以文章开始的示例为例进行析因分析,步骤如下。适用条件可直接利用原始数据进行考察,可利用本例Save对话框生成残差并保存为新变量,然后考察残差的正态性和方差齐性,具体操作略。
【1】数据录入:利血平(lxp)和新药(newD)各看成一个因素,每个因素都有2个水平(0:不用药;1:用药)。

【2】方差分析:Analyze>>General Linear Model>>Univariate…
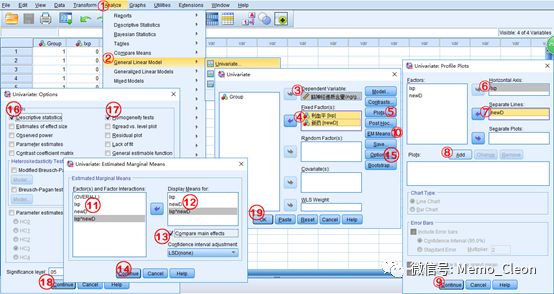
Model…对话框默认是全因子分析,完全随机设计、区组设计、交叉设计及拉丁方设计的方差分析不考虑交互作用,在使用单变量(Univariate)过程构建分析模型时,只选择主效应。本例为析因设计,进行各个因素及其交互作用的分析,可以直接默认为全因子分析。值得注意的是,默认的全因子分析包括各个因素(Factor)及其之间的相互作用分析,并不包含协变量(Covariate)与因素(Factor)之间的交互作用,因此如果要协变量与因素之间的交互作用,需要在Model…对话框自定义选入。
【3】结果及解读
(1)受试者间因素概况
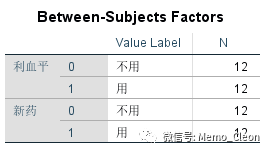
(2)描述性统计量。各因素个水平的原始均值、标准差及案例数。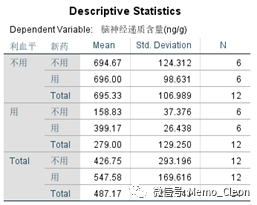
(3)方差齐性检验。F=2.311,P=0.107>0.05,方差齐同。
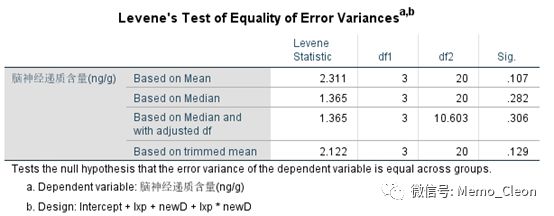
(4)受试者间效应检验。模型有统计学意义,说明至少有一个分析因素系数不为0,可以使用该模型进行分析。利血平(lxp)和新药(newD)的主效应均有统计学意义,但由于两者的交互作用(lxp*newD)存在交互作用,两个因素主效应有无统计学意义已经没有实际价值,需要进一步分析某个因素在另外一个因素的各个水平上的差异,即按照不同的组合来进行分析。利血平和新药的交互作用(F=12.564,P=0.002<0.05),新药的单独效应随利血平的不同水平而变化,结合后面的轮廓图可以判断,新药可能对利血平有拮抗作用。
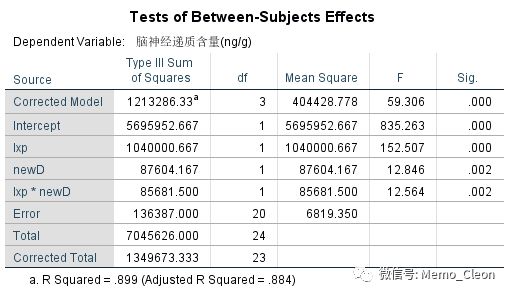
(5)边际均数。如受试者间效应检验结果所言,利血平和新药存在交互作用,这种利用边际均数的两两比较已无多大使用价值,本例此部分结果仅做演示。
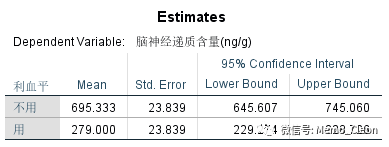
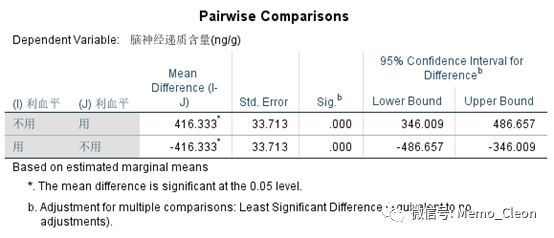
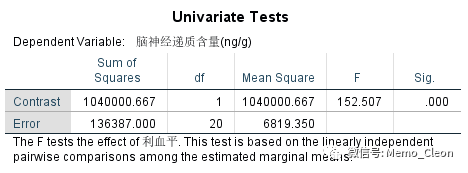
(5.1)利血平组的估计值、成对比较及方差分析结果。使用利血平比不用利血平的脑神经递质含量更低,且两者有统计学意义。
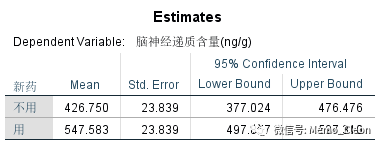
(5.2)新药组的估计值、成对比较及方差分析结果。使用新药比不用新药的脑神经递质含量更高,且两者有统计学意义。
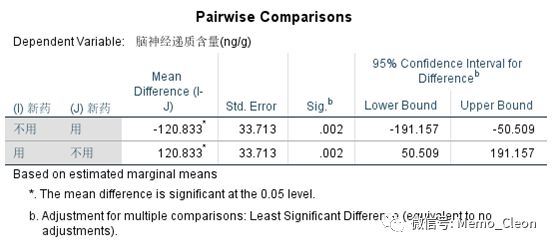
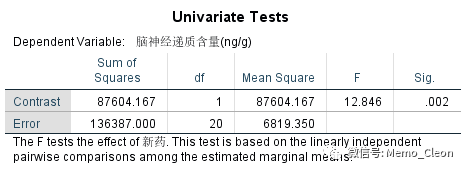
(5.3)利血平和新药的交互作用(利血平*新药)。不用利血平的前提下,使用新药比不用新药的脑神经递质含量略高;使用利血平前提下,使用新药比不用新药的脑神经递质含量更高。但是否有统计学意义不能判断。
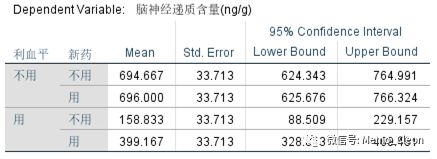
(6)轮廓图。利血平的水平不同,新药的边际均数也不同,提示可能存在交互作用;两要联合后边际均数升高,提示新药可能对利血平的降递质作用有拮抗效果。
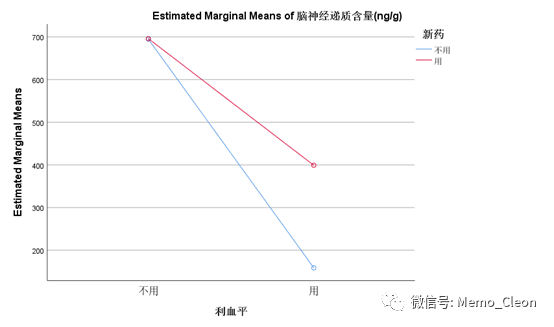
【4】单独效应检验。受试者间效应检验表明利血平和新药存在交互作用,需要进一步对不同因素的各个水平进行比较,SPSS中有三种方法可以实现。①LMATRIX子句;②EMMEANS子句;③重新设定分组,采用单因素方差分析后使用Post HOC或者EMMEANS对话框来实现。其中①和②需要借助程序编辑器。下面依次介绍这三种方法。
在Univariate…过程的最后一步,点击“Paste”金瑞程序编辑器。
①LMATRIX子句(红框内内容为输入内容)如下,完成后点击运行即可。
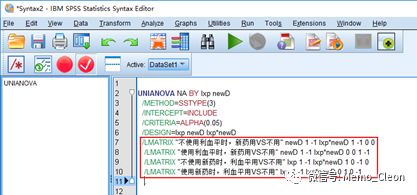
②EMMEANS子句(红框内内容为输入内容)如下,完成后点击运行即可。
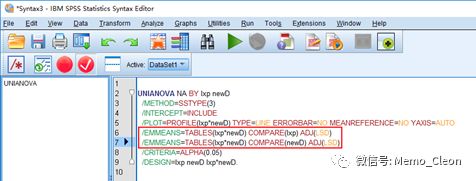
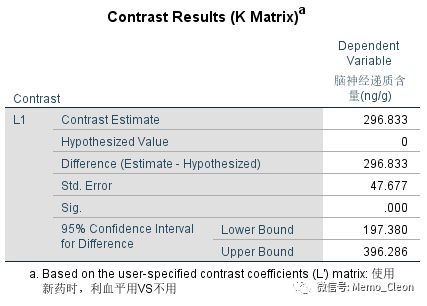
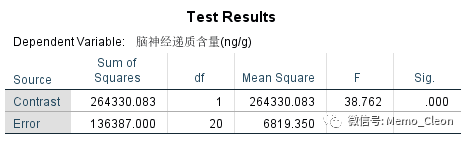
LMATRIX子句的运行结果首先输出自定义假设检验的索引,接着分别输出各个组合间的检验结果,包括比对和方差分析结果。
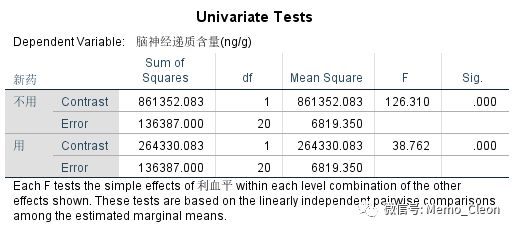
当不使用利血平时,不用新药(空白对照组)和使用新药(新药组)结果如下,样本均数差值为-1.333,P=0.978,这个结果与使用单因素方差分析事后多重比较的LSD分析的结果一致。即当不使用利血平时,不用新药(空白对照组)和使用新药(新药组)没有显著的统计学差异,其后的方差分析与该结果一致。
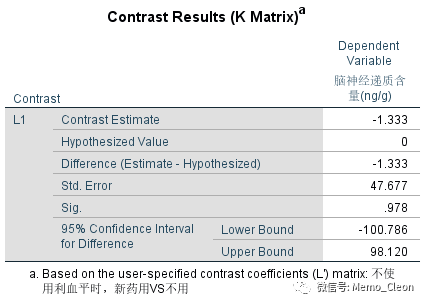
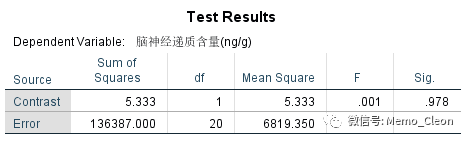
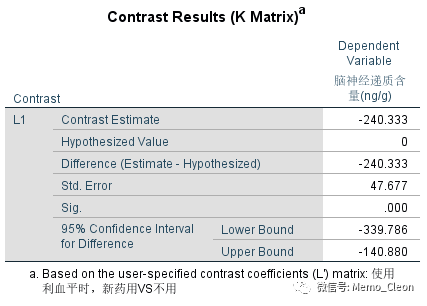
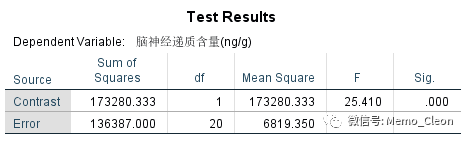
使用利血平时,不用新药(利血平组)和使用新药(联合用药组)差异具有统计学意义(P<0.001)。
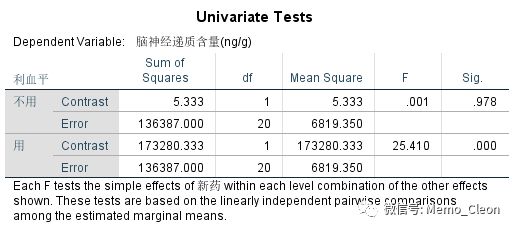
不使用新药时,不用利血平(空白对照组)和使用利血平(利血平组)差异具有统计学意义(P<0.001)。
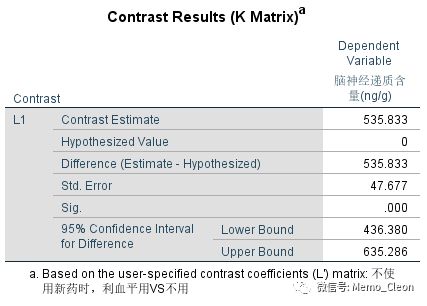
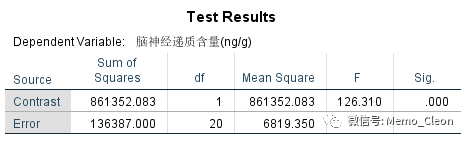
使用新药时,不用利血平(新药组)和使用利血平(联合用药组)差异具有统计学意义(P<0.001)。
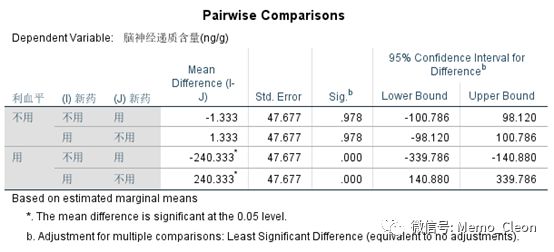
MMEANS子句在一个表格中直接输出利血平和新药各种水平组合的边际均数的估计值、成对比较和方差分析结果。结果同LMATRIX子句结果完全一致,不再累述。
利血平*新药
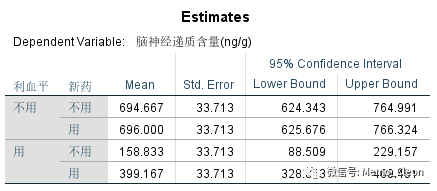
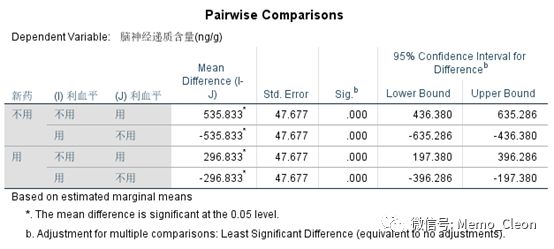
新药*利血平

③除使用上述程序对单独效应进行检验外,也可对数据重新设定组,将lxp、newD两因素的各个水平进行组合,每个组合为1组,本例可以组合为4组,然后进行单因素的方差分析,其后的事后检验(Post Hoc)或者利用边际均值(EMMEAN)检验,也可以得到相同的结果。本文一开始就是使用的单因素方差分析,然后进行了事后检验,结果和使用程序进行检验的结果是一致的。
后记:几个概念的介绍和理解
(1)析因设计的方差分析可将总变异分解为:处理间效应和误差项,其中处理间效应细分为每个因素的主效应、各因素的交互作用。
以两因素(A、B)为例,离均差平方和SS总=SS处理+SS误差=SSA+SSB+SSAB+SS误差
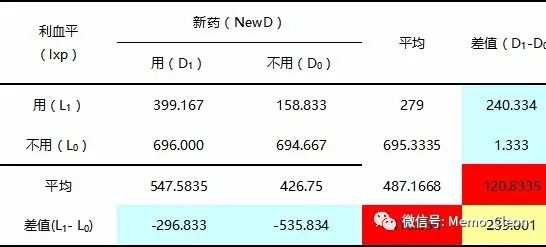
①单独效应/简单效应:其他因素的水平固定时,某因素不同水平间的差别。
lxp在L1水平时,newD的单独效应:399.167-158.833=240.334;
lxp在L0水平时,newD的单独效应:696-649.667=1.333。
同理,newD在D1水平时,lxp的单独效应:399.167-696=-296.833;
newD在D0水平时,lxp的单独效应:158.833-694.667=-535.834。
②主效应:某因素各个水平单独效应的平均
newD的主效应:(240.334+1.333)/2=120.834;
lxp的主效应:(-296.833-535.834)/2=-416.334。
③交互作用:一个因素在不同水平时,另外一个或几个因素的单独效应不同,即各因素之间存在不独立的情形。无交互作用可以直接对主效应进行解释,但如果存在主效应,需要分析每个因素的单独效应。
newD*lxp=(-296.833+535.834)/2
=lxp*newD=(240.334-1.333)/2
=239.001/2=119.501
(2)模型检验:轮廓图(Plots对话框)、残差图(Options对话框:Residual plot)及失拟检验(Options对话框:Lack of fit,当前模型与全模型是否有统计学差异)。


