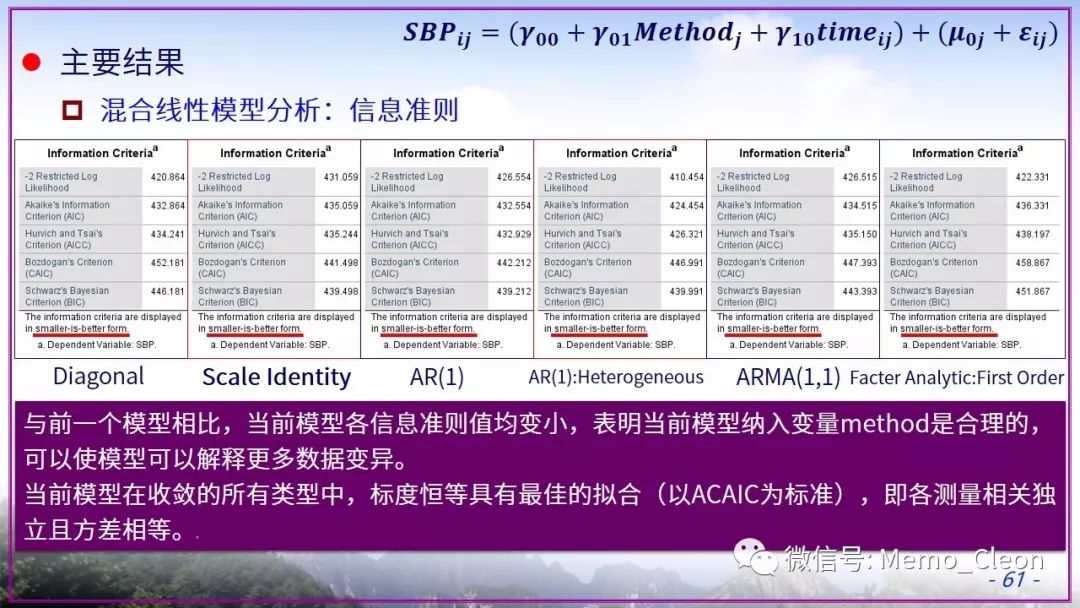
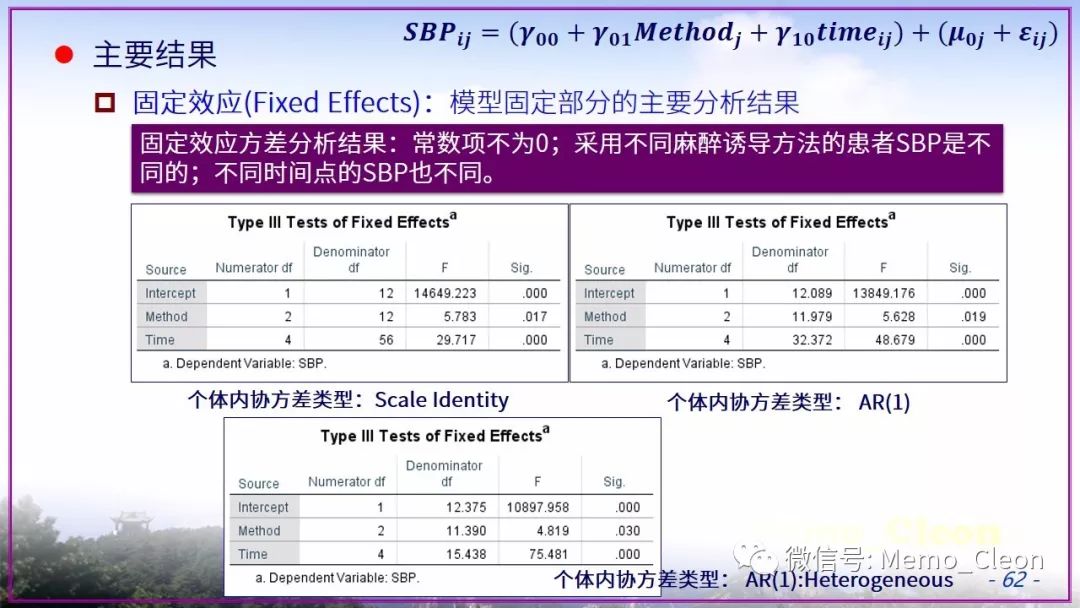
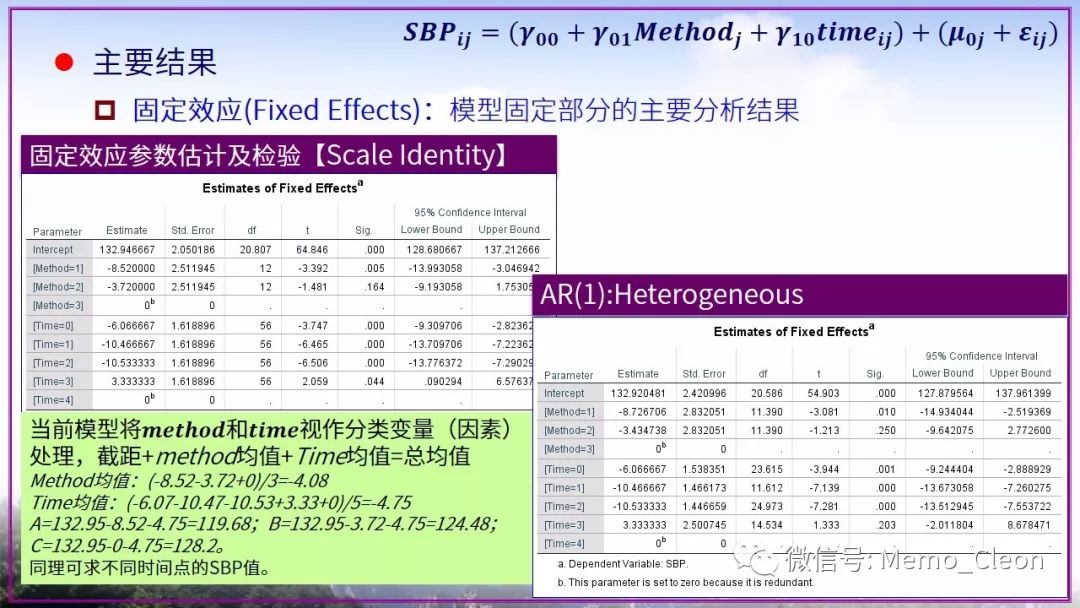
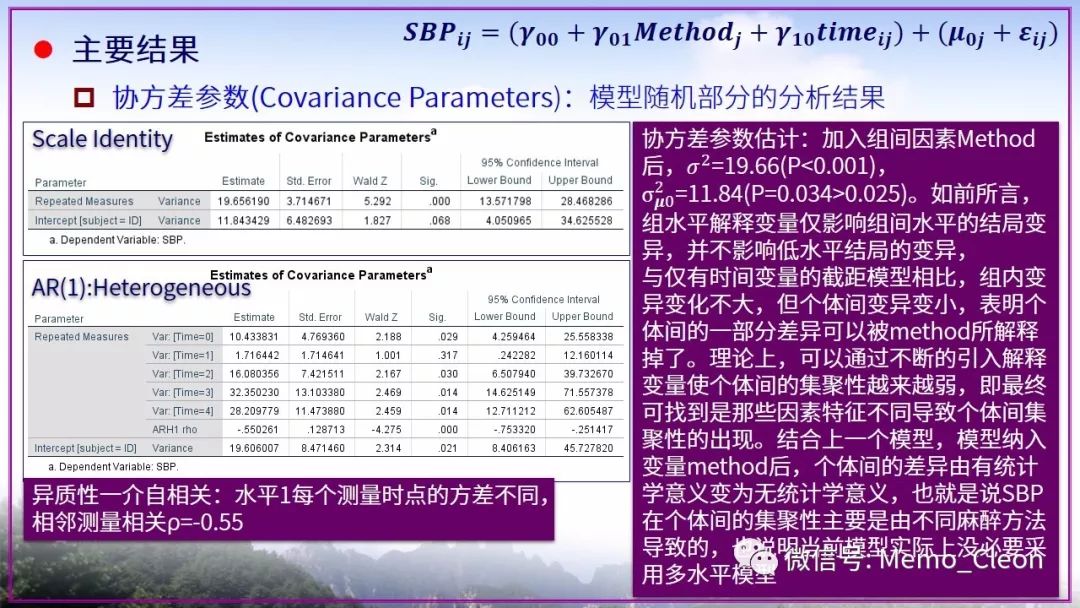
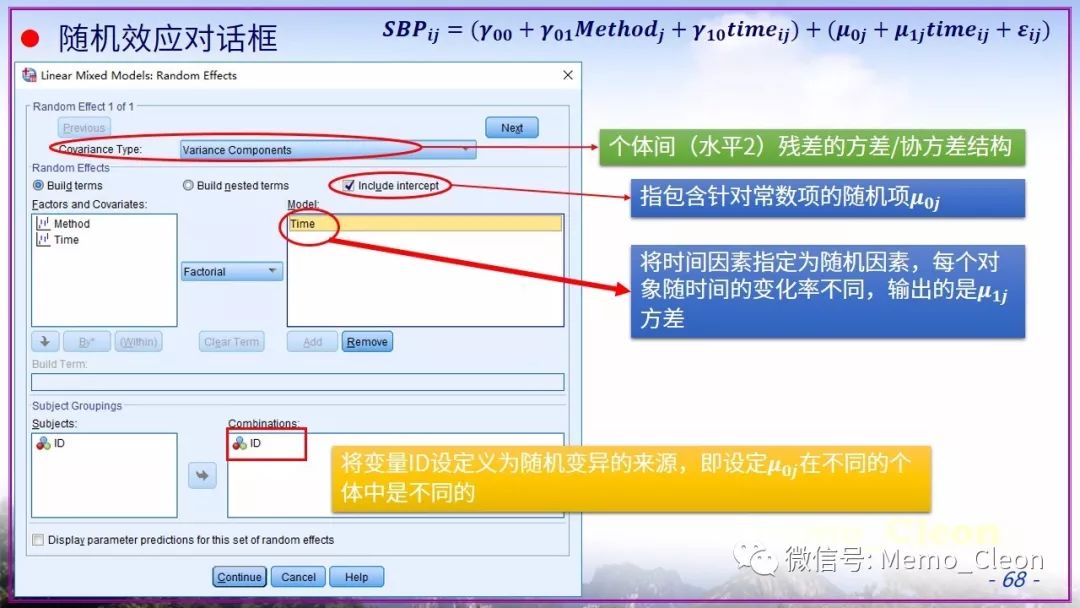
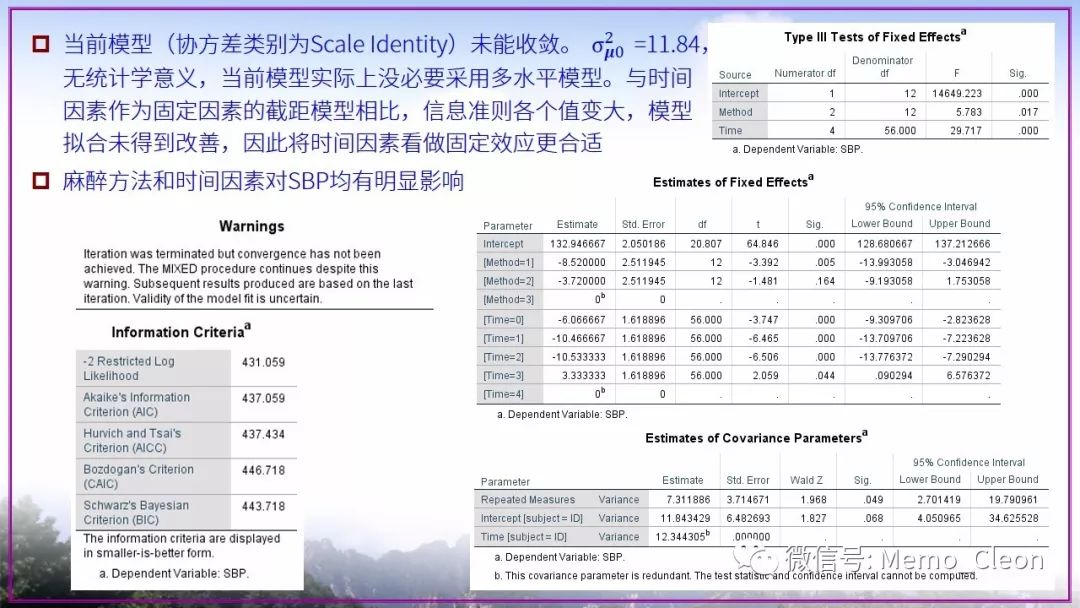
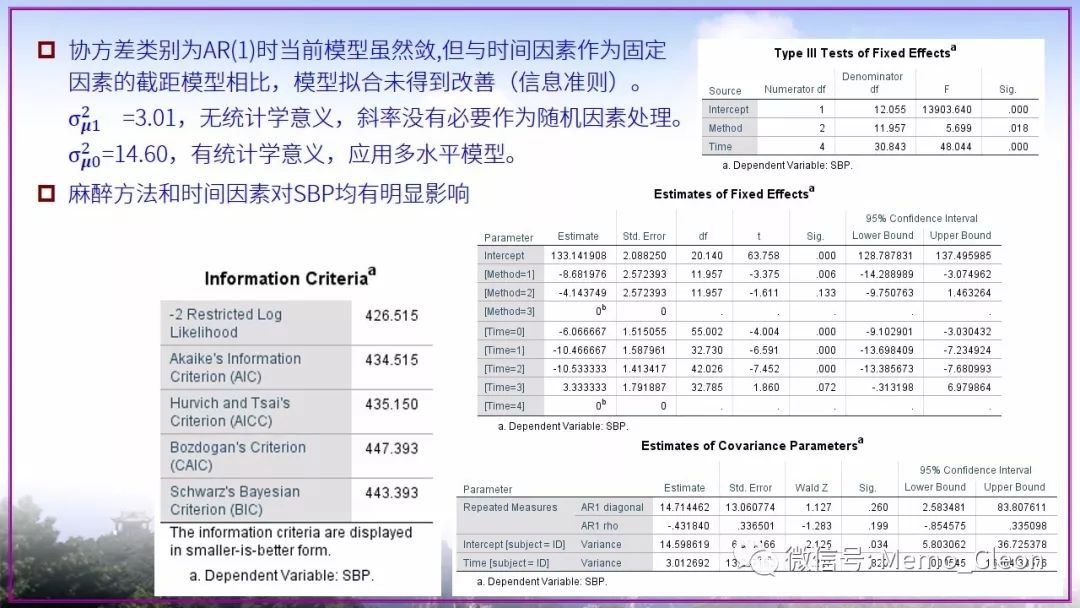
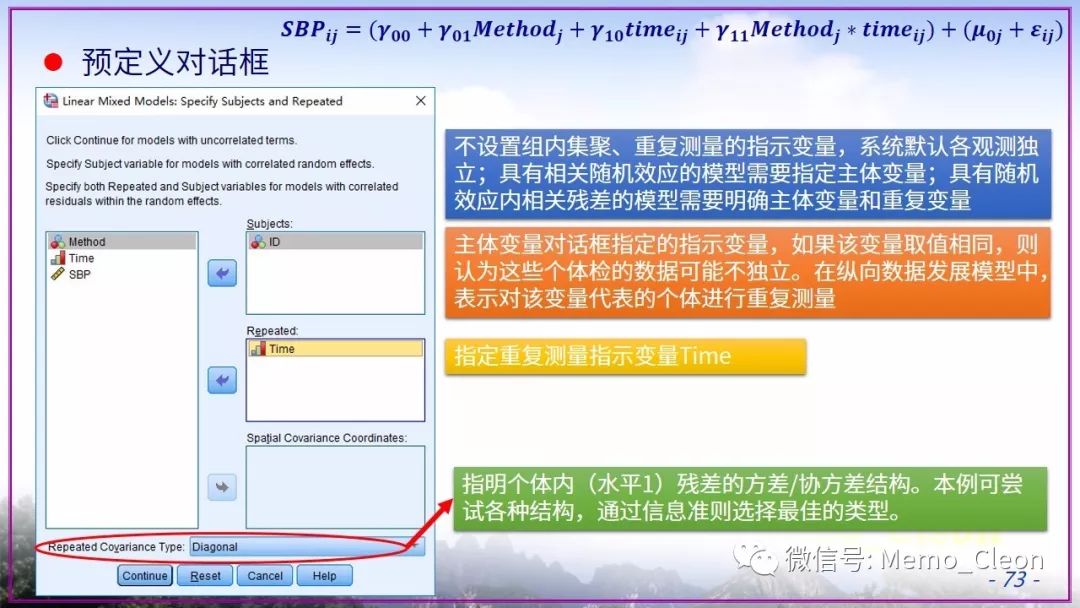
线性混合模型是个大工程,憋了许久依旧存在众多不解的问题。本示例选择极不恰当,因此本次笔记也仅作为演示混合线性模型的操作步骤的一个草稿。
分层数据是医学研究设计中常见的数据形式,比如多中心临床试验数据,这种数据一般某个中心内的患者具有一定的相关性(组内同质),但不同中心的患者保持独立(组间异质),这种横向数据可以用多水平模型进行分析。
医学研究中还有一种较常见设计就是长期跟踪研究对象,对同一研究对象反复收集数据,这种按时间顺序对研究对象进行重复测量得到的数据叫纵向数据,纵向数据也可以用多水平模型进行分析。研究对象是高水平(水平2,宏观水平,个体间),研究对象内的不同测量是低水平(水平1,微观水平,个体内)。纵向数据的多水平模型又称发展模型。纵向数据有几个明显的特征:①研究中需要对每一个对象反复收集数据,因此个体内观测值存在相关性,②纵向数据有两种变异来源:个体内变异和个体间变异,两种变异又可能随时间变化,③纵向数据通常存在各种原因的“失访”。
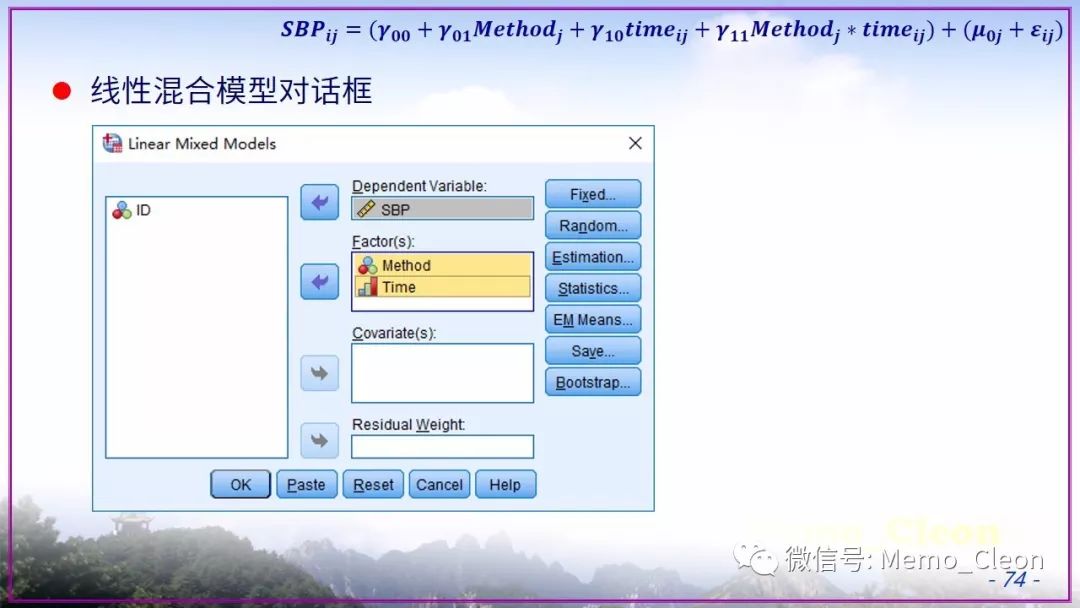
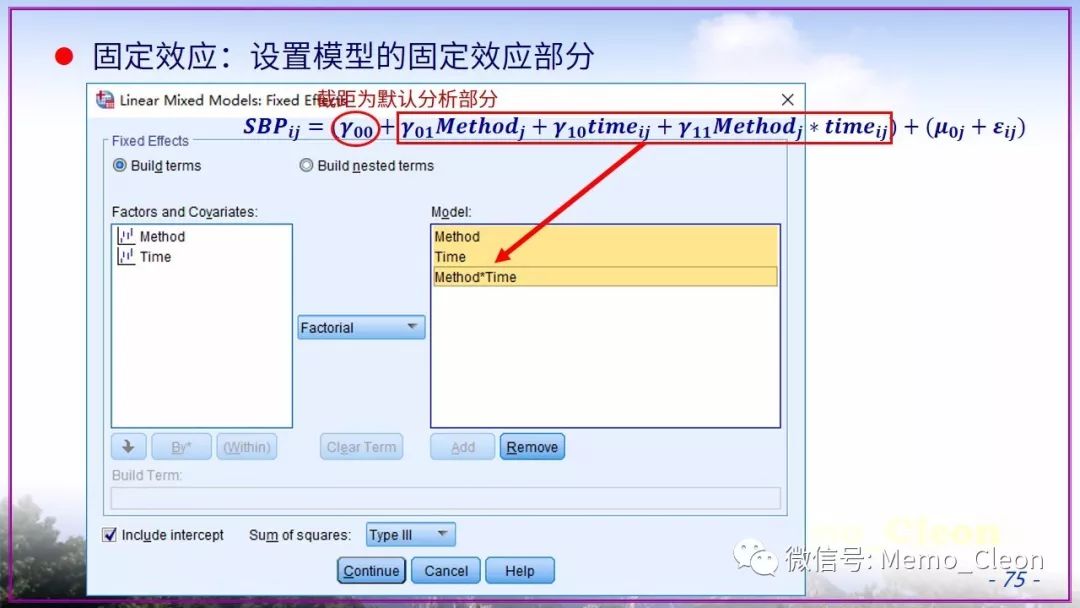
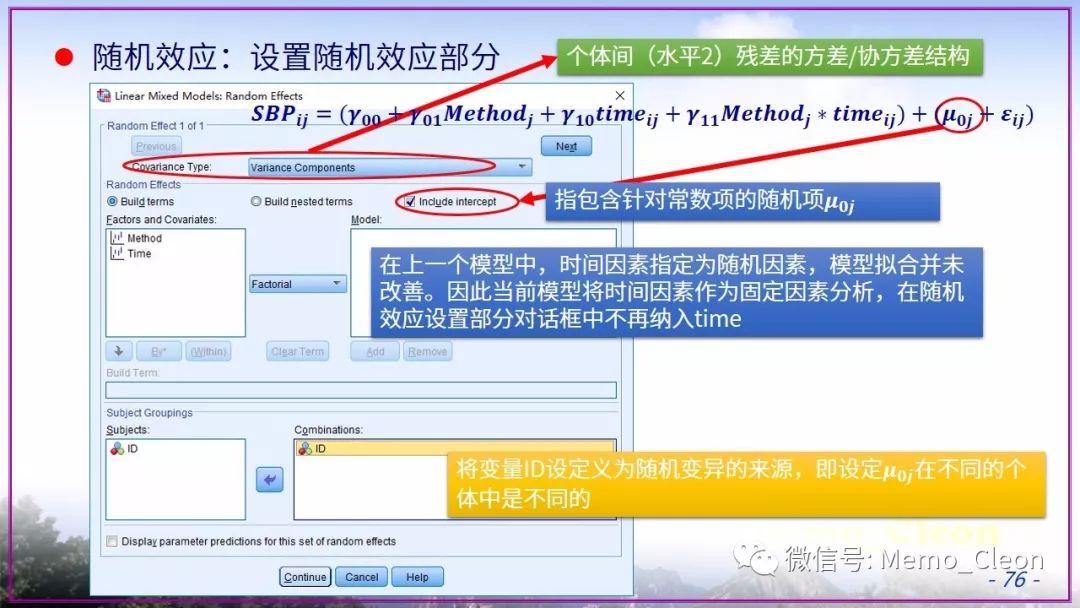
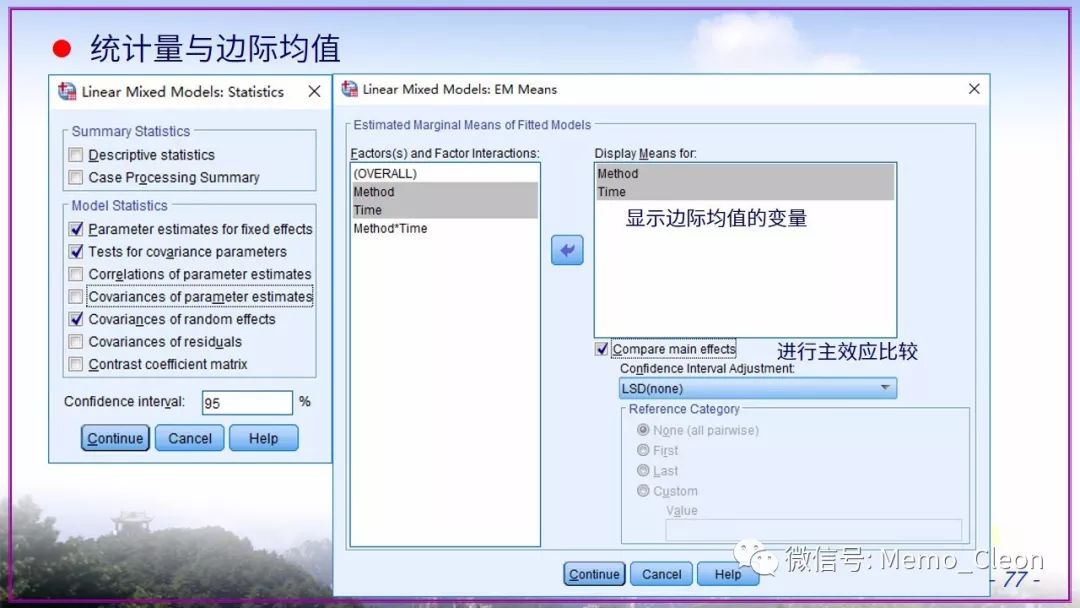
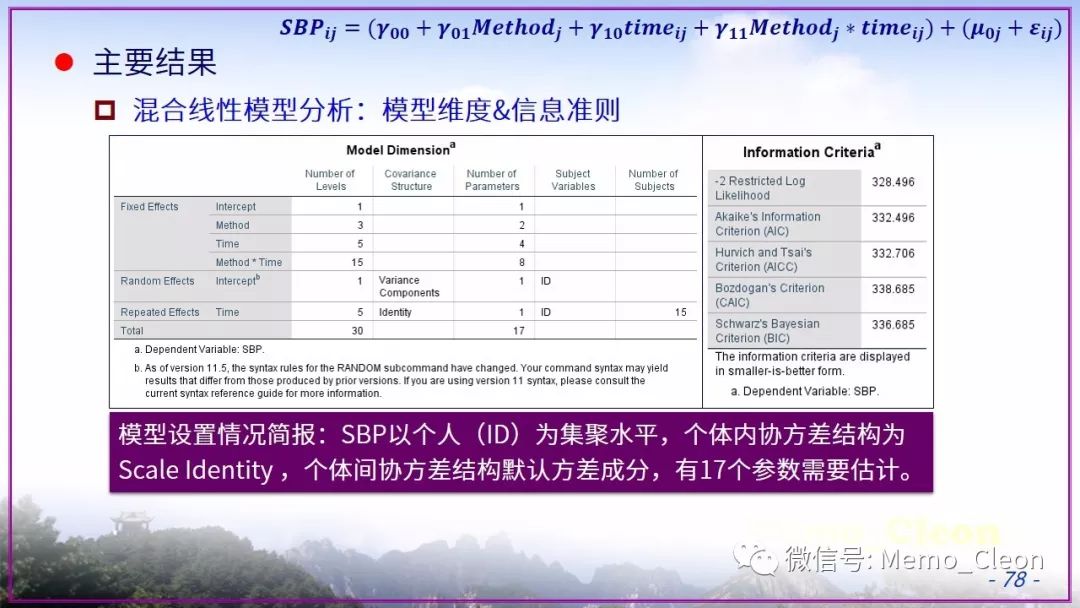
混合线性模型示例


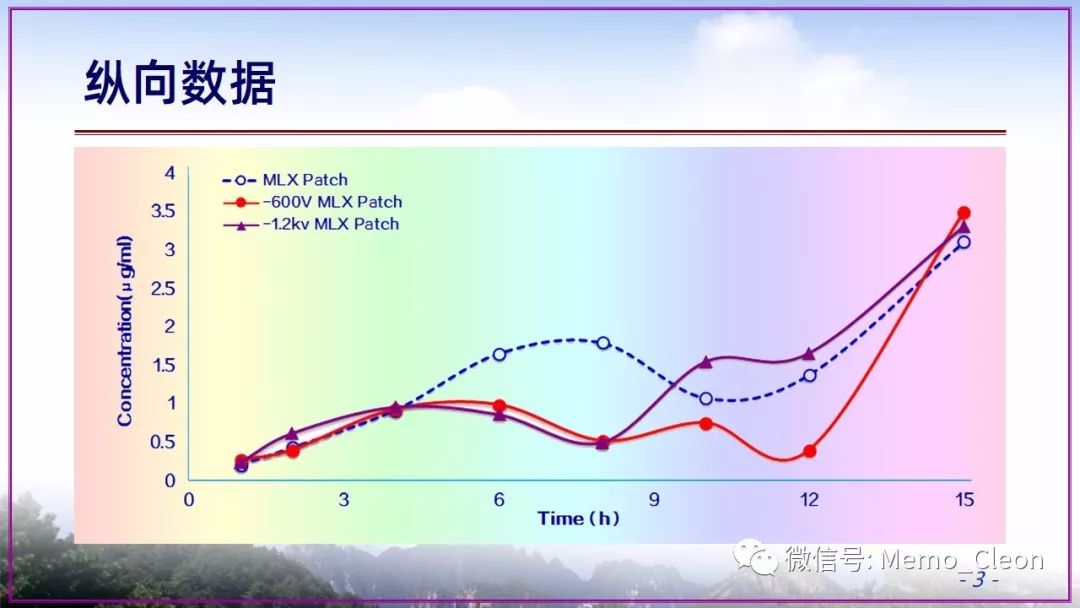






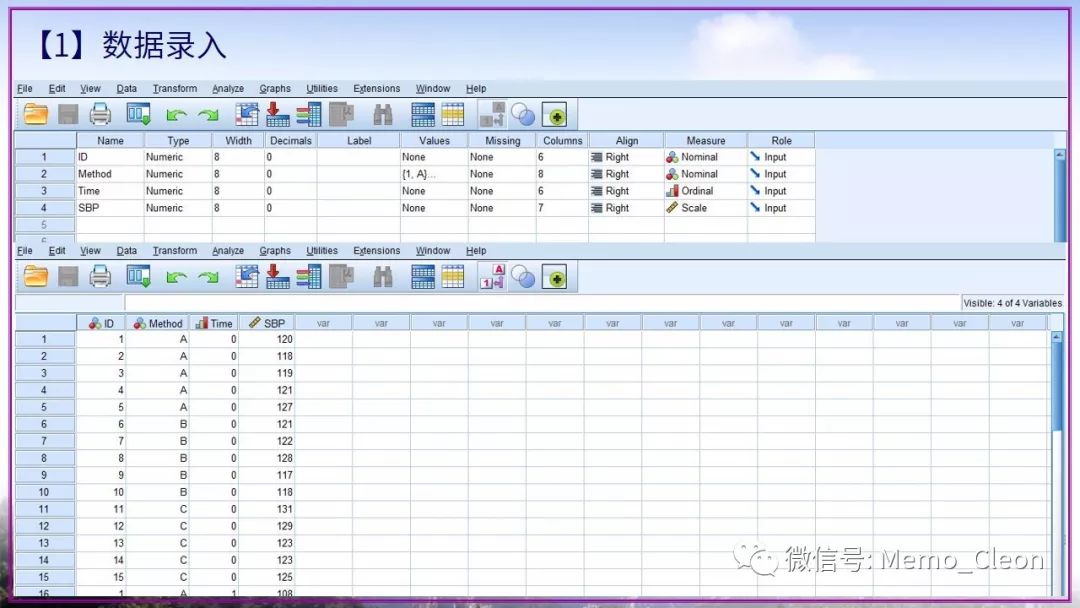
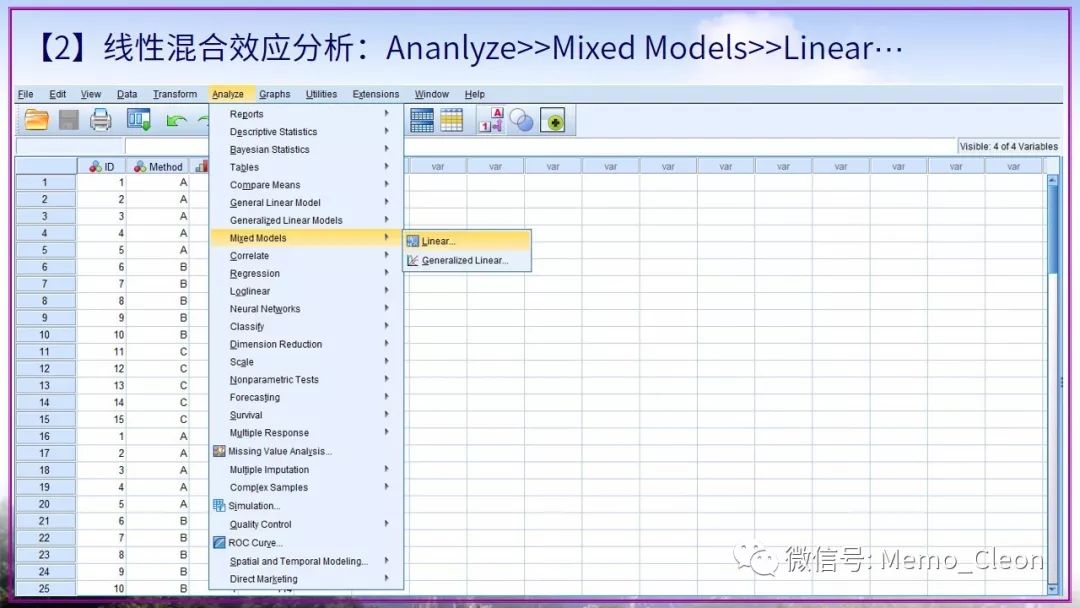

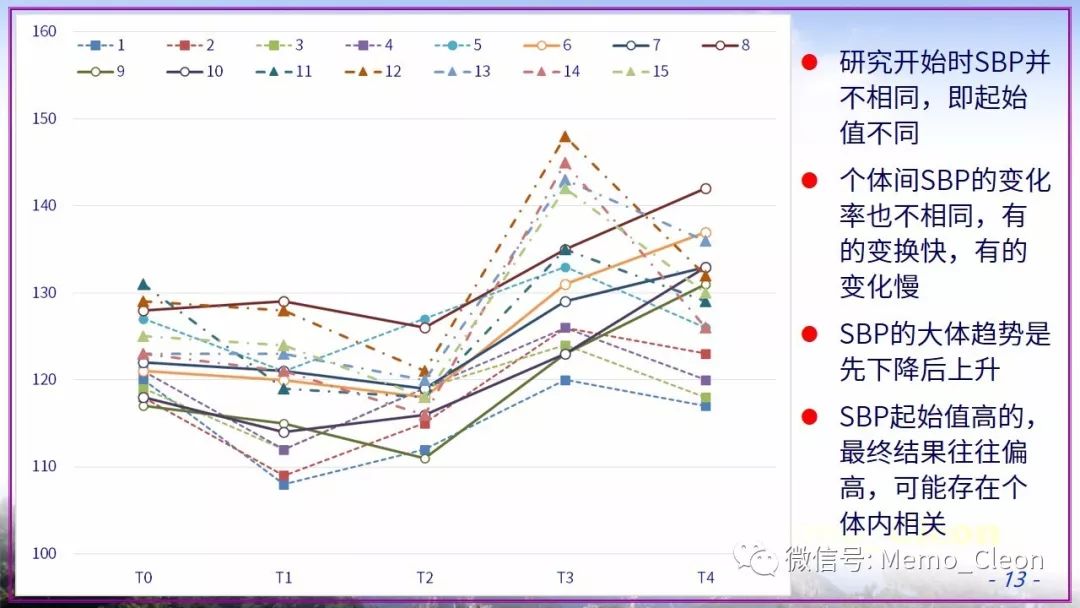
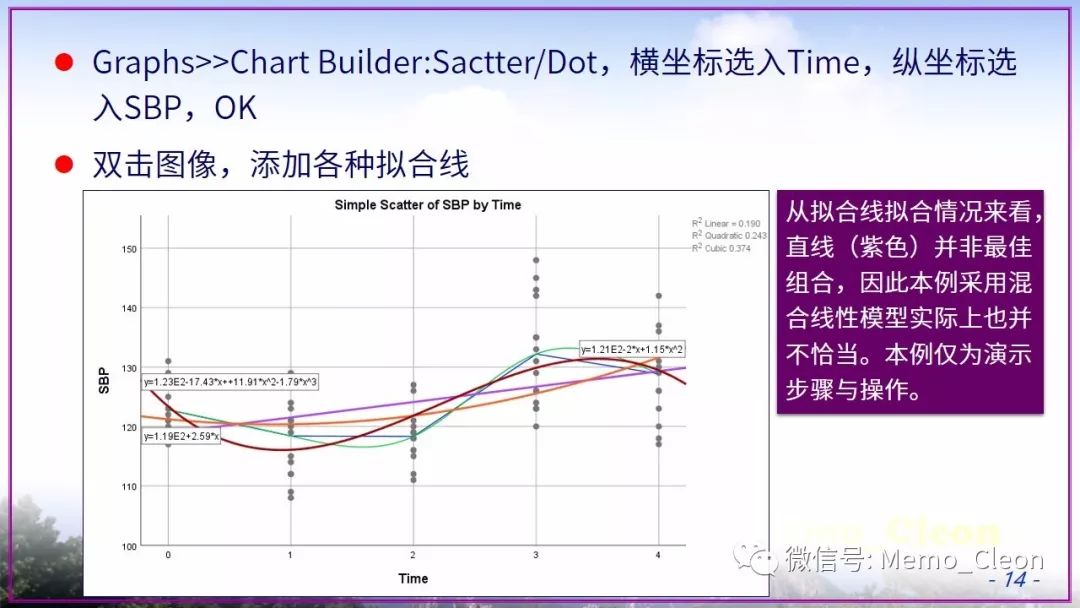
除了以上直接用上述的图示法大体判断外,还可以使用定量的统计检验来进行。在拟合模型前,需要先对变量进行编码。


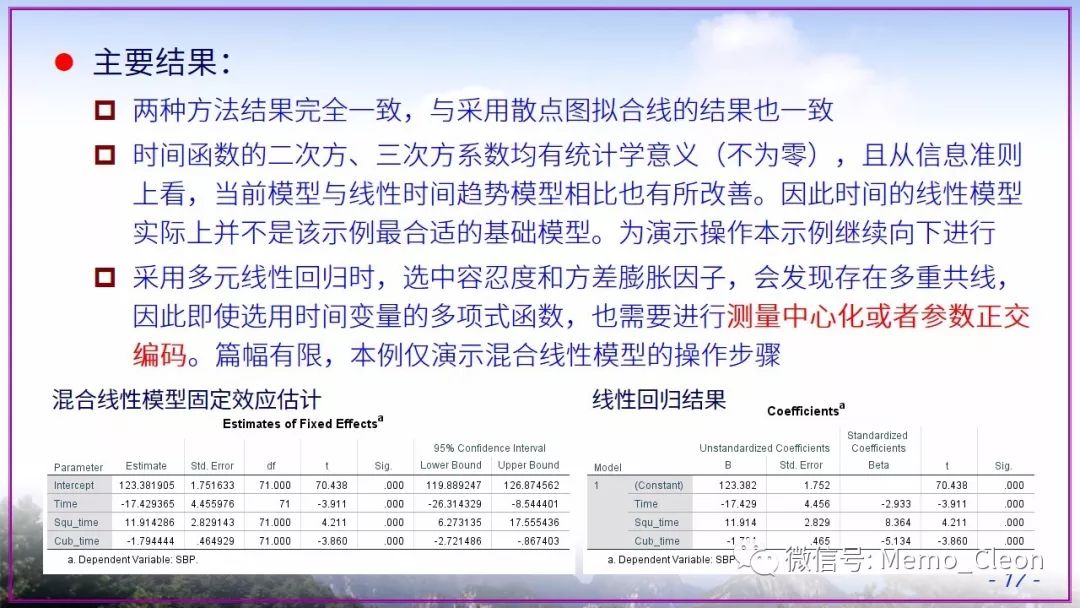
但数据中的解释变量的零值无意义时,应考虑对该变量进行中心化处理。另外,具有随机效应的变化率与截距相关时(协方差不为0),可能会引起较强的共线性,此时也需要中心化处理。本例为进行中心化。
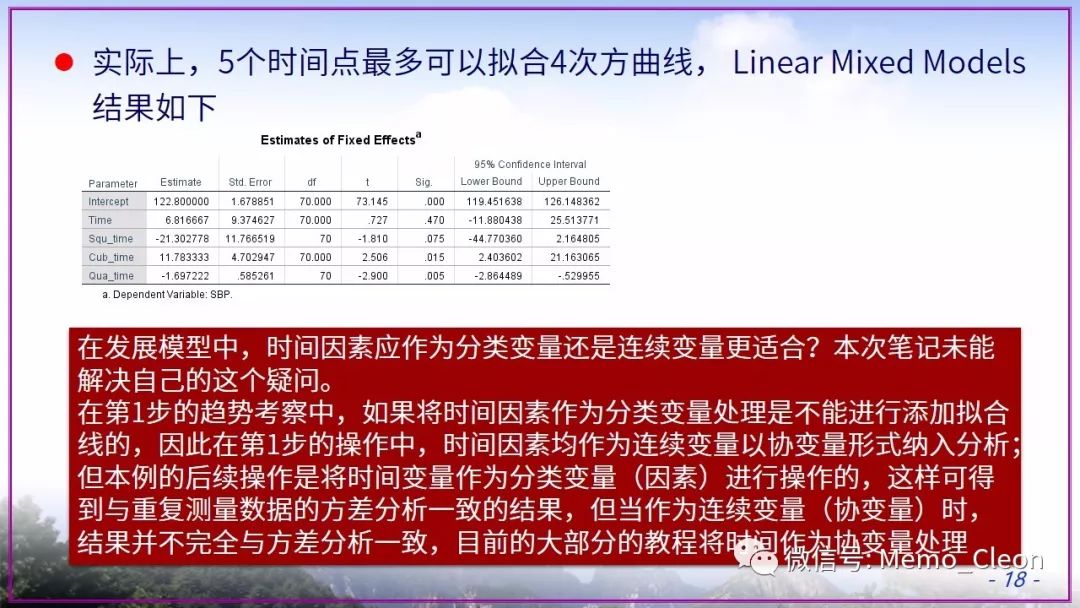



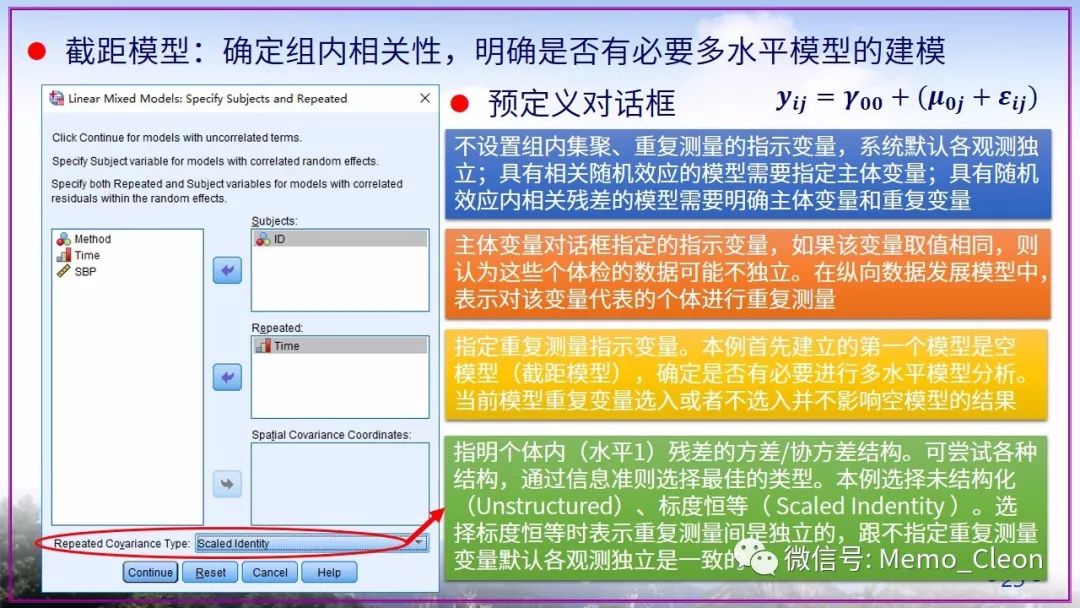

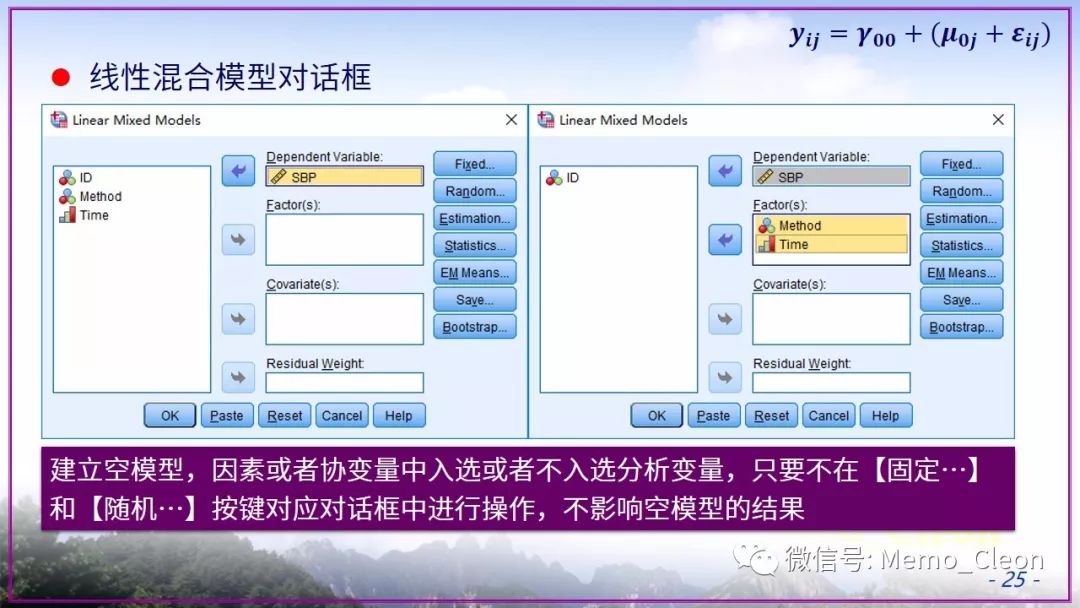
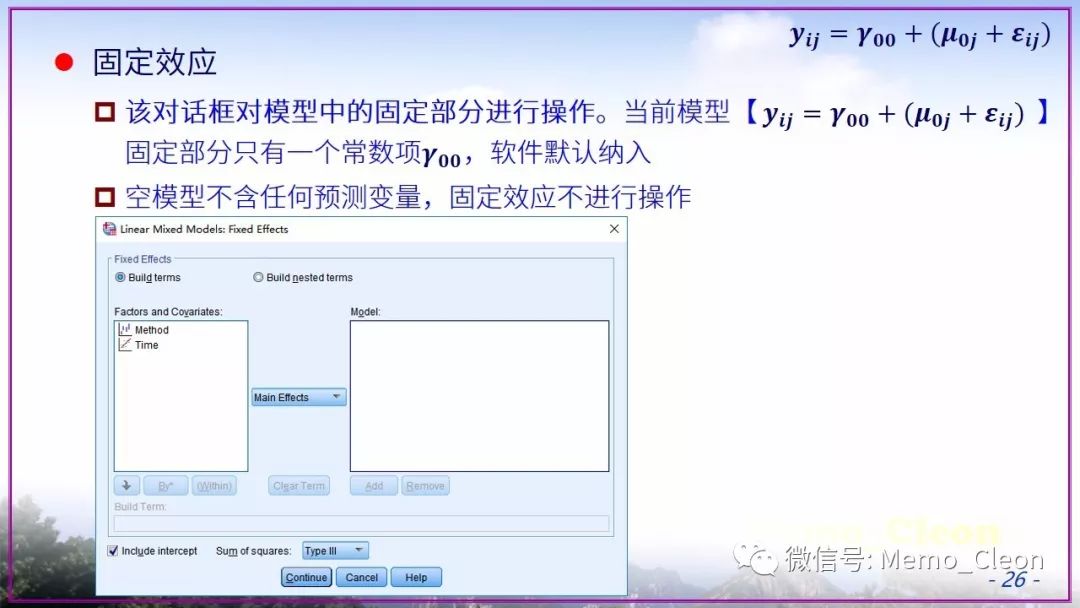
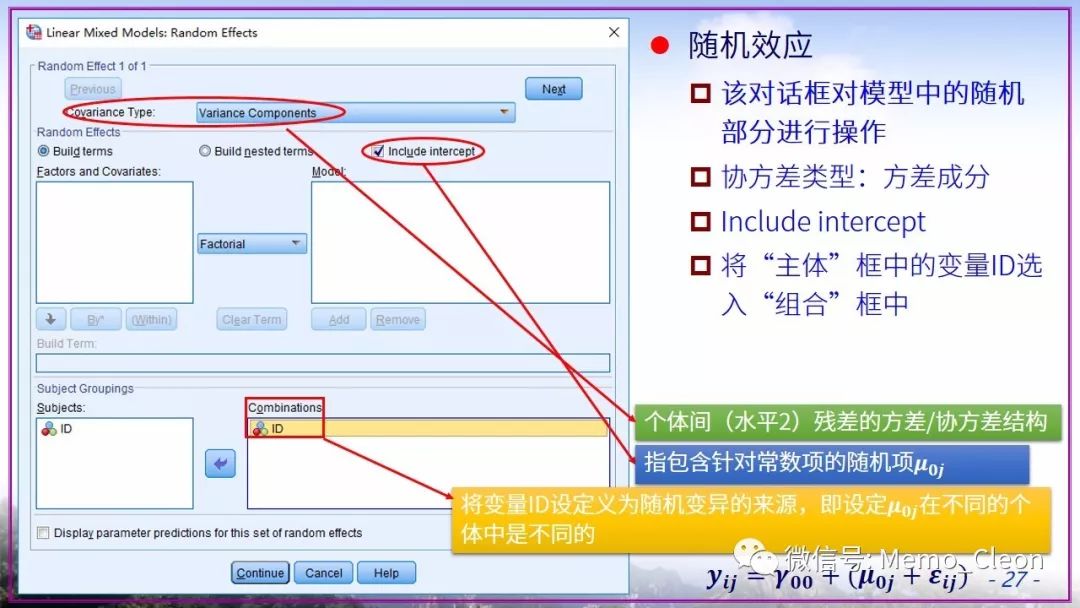
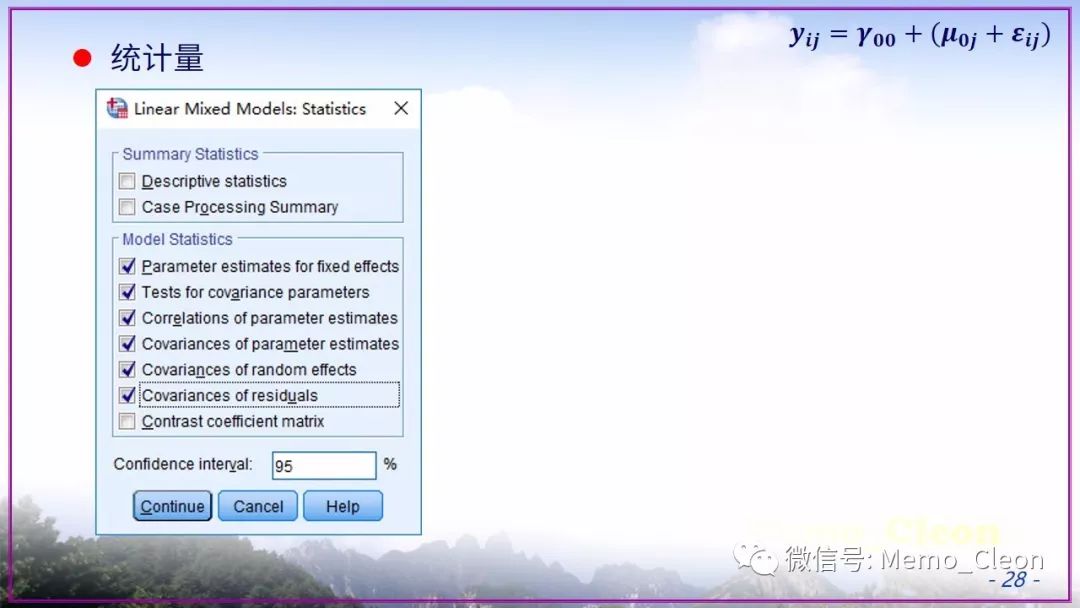




本示例后面也一直使用了默认的REML,在适合使用ML的时候也没有在【估计】对话框中修改,原因只有一个:懒!

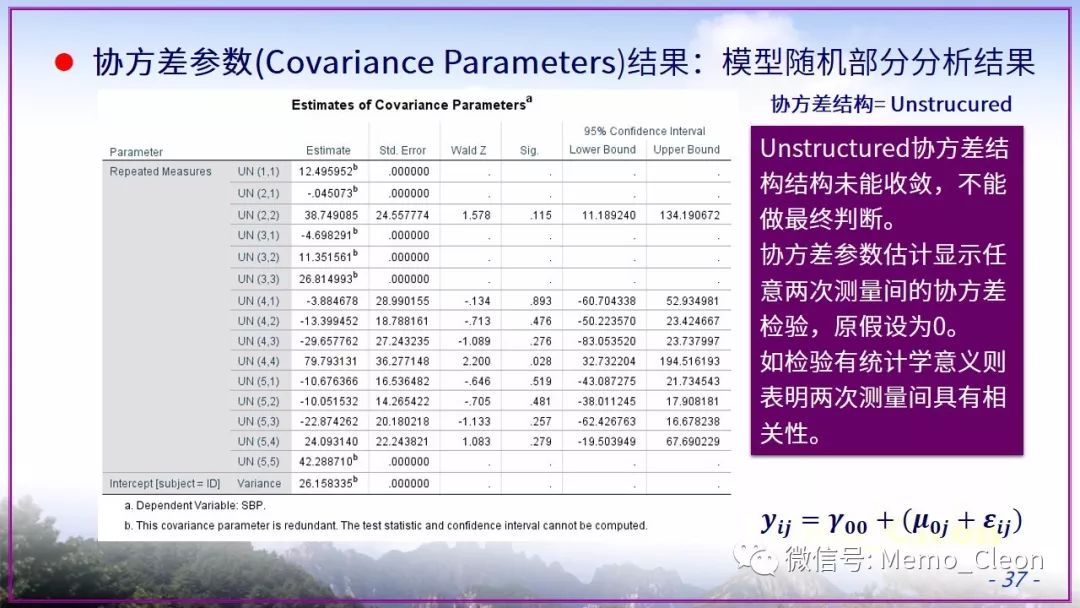
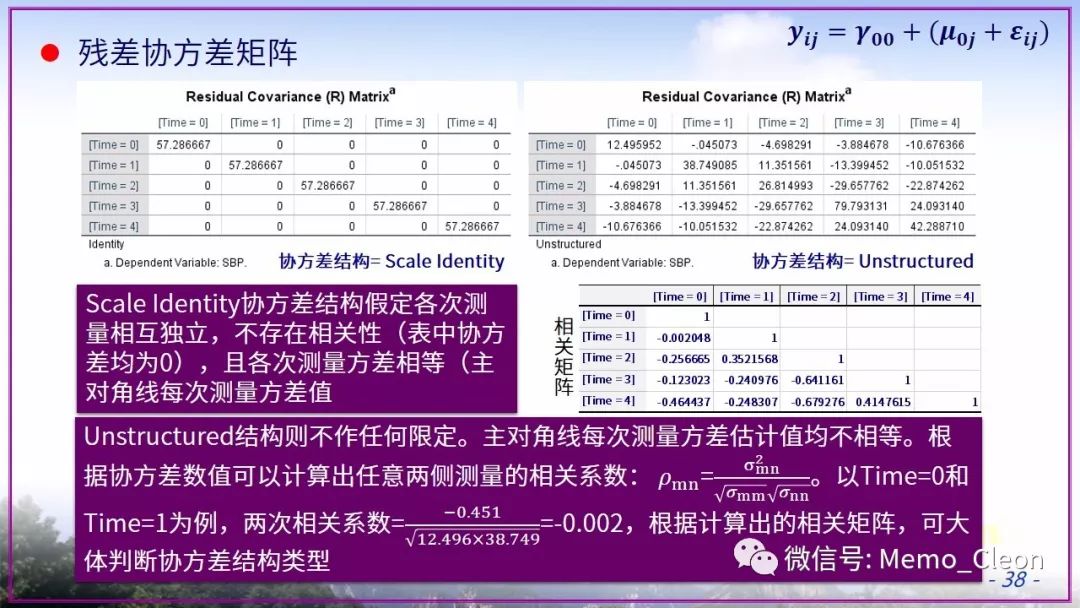
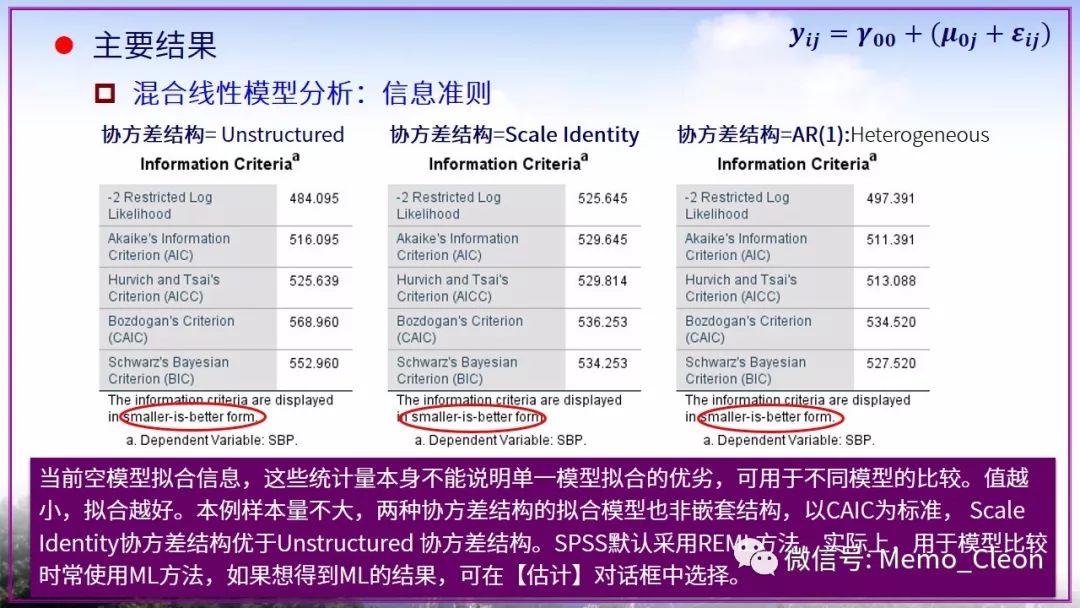
通过 不做限定的无结构化协方差结构 得出的R矩阵 以及由此计算出的相关矩阵 可以用来寻找合适的协方差结构,可惜我看不出来,只能通过尝试各种结构来寻找最佳拟合。



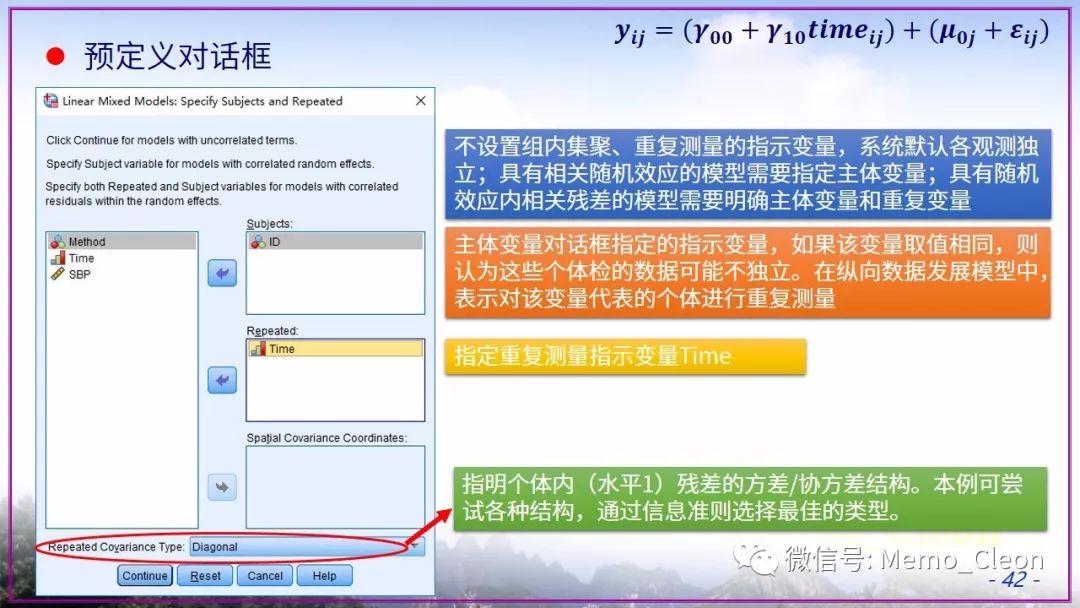
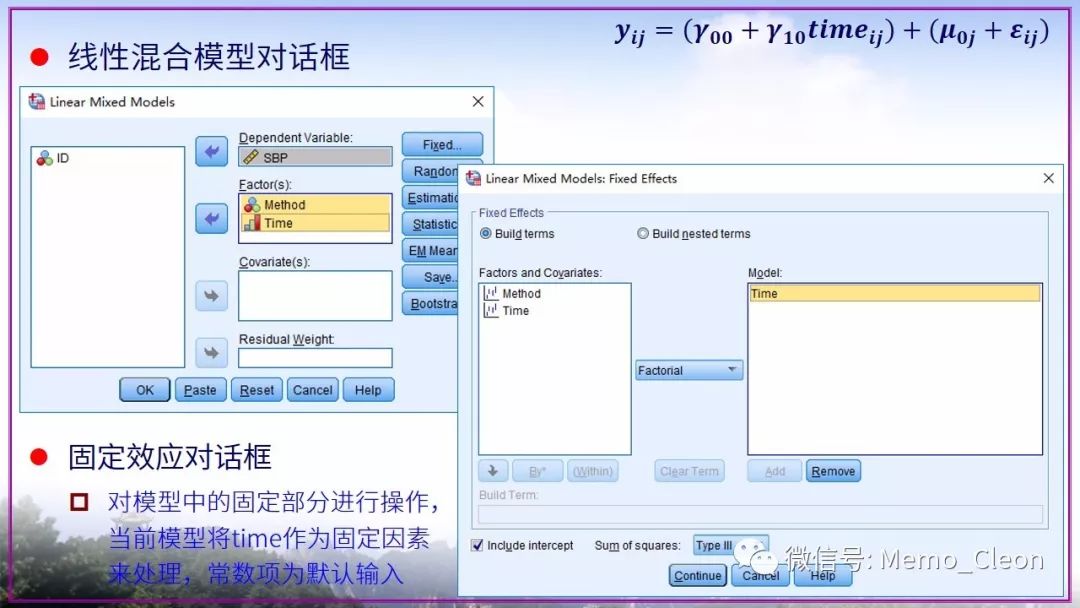
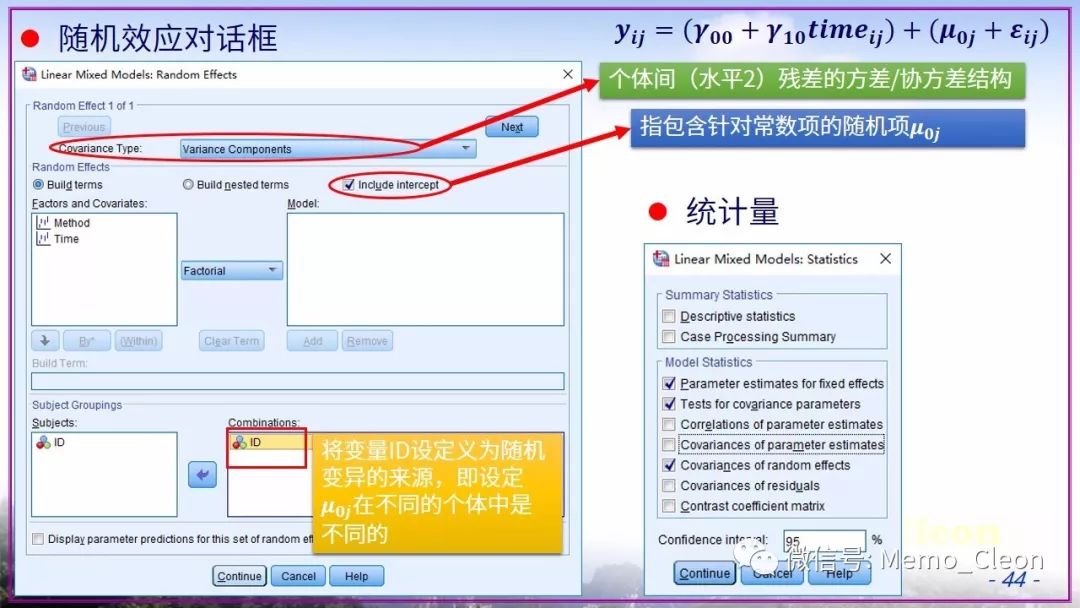
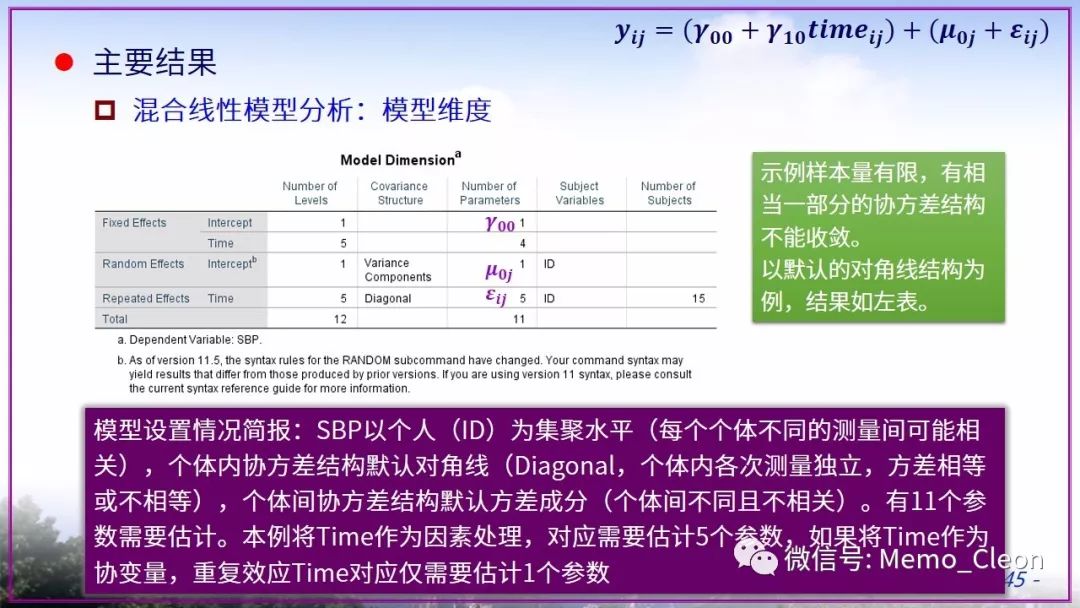
又懒了……
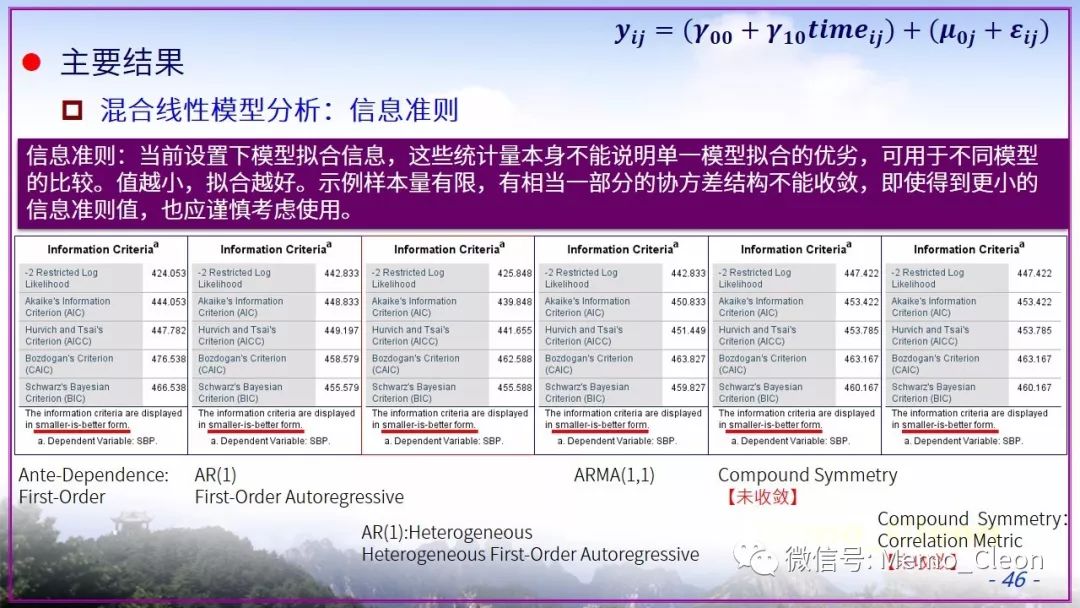
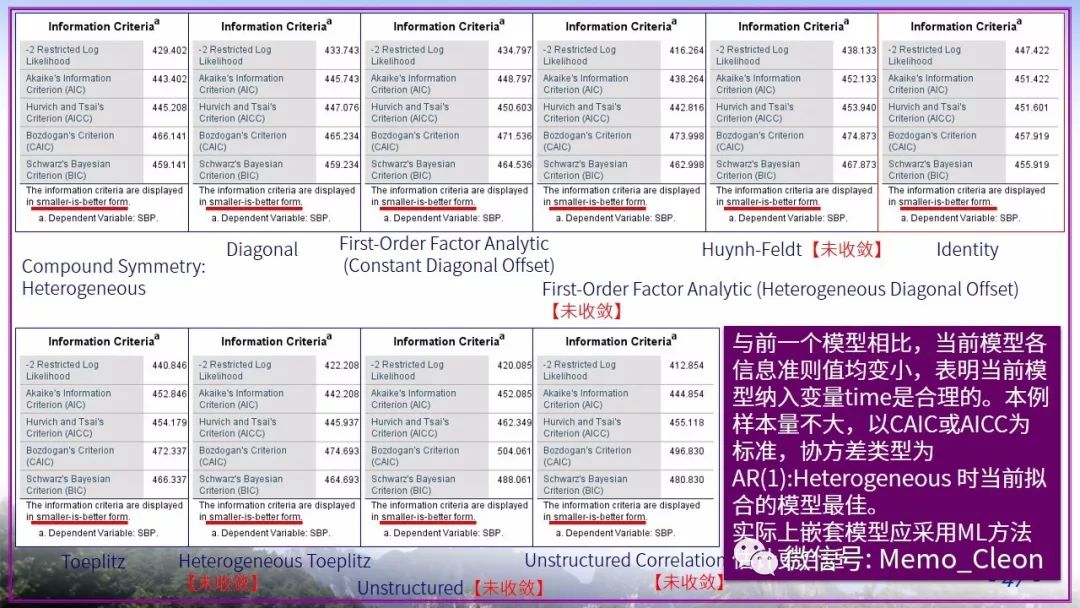




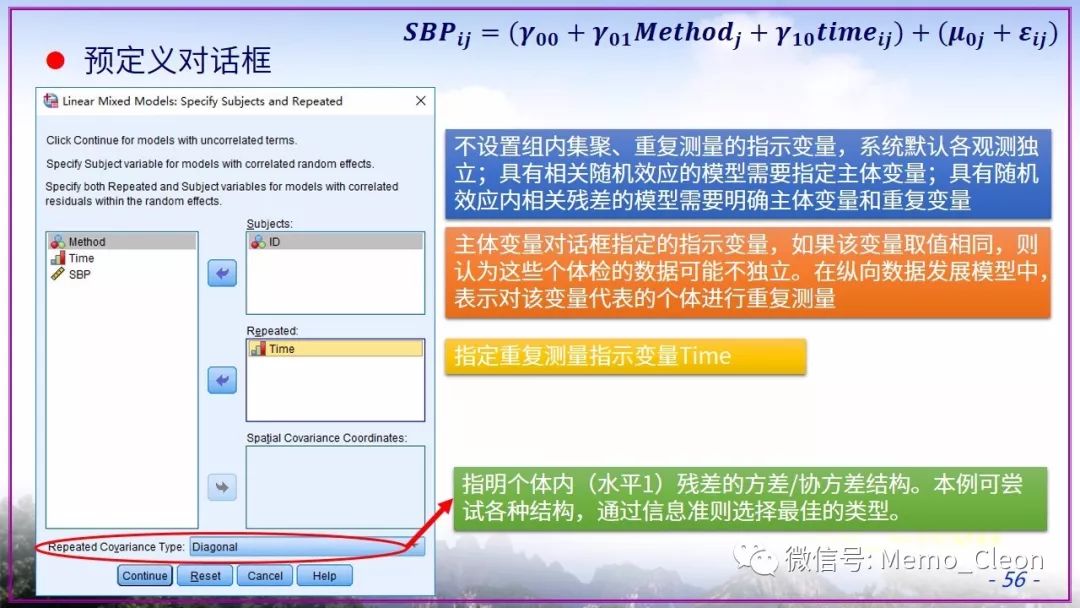
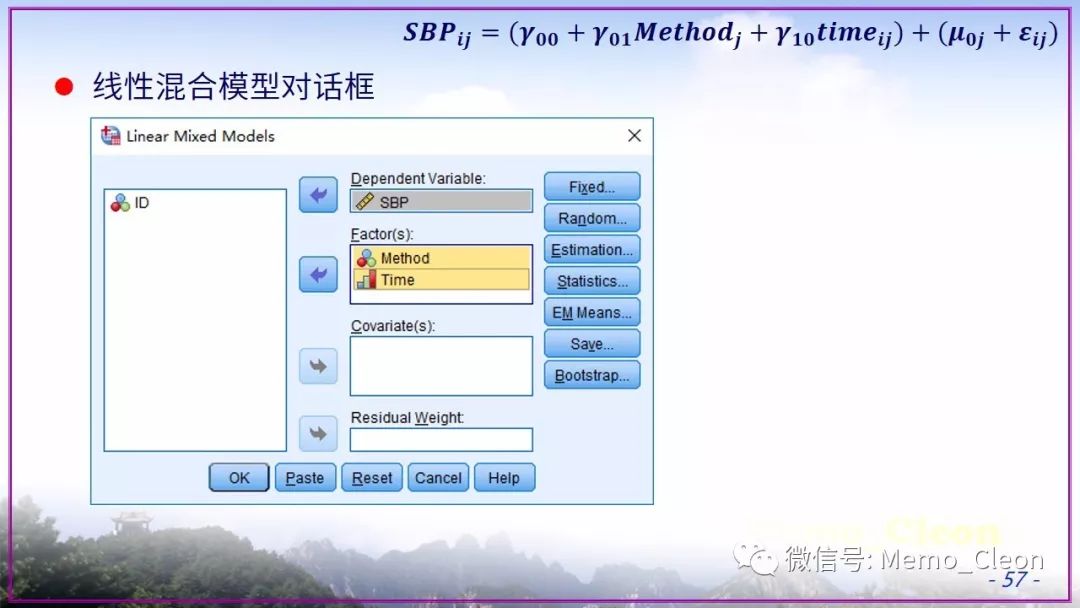
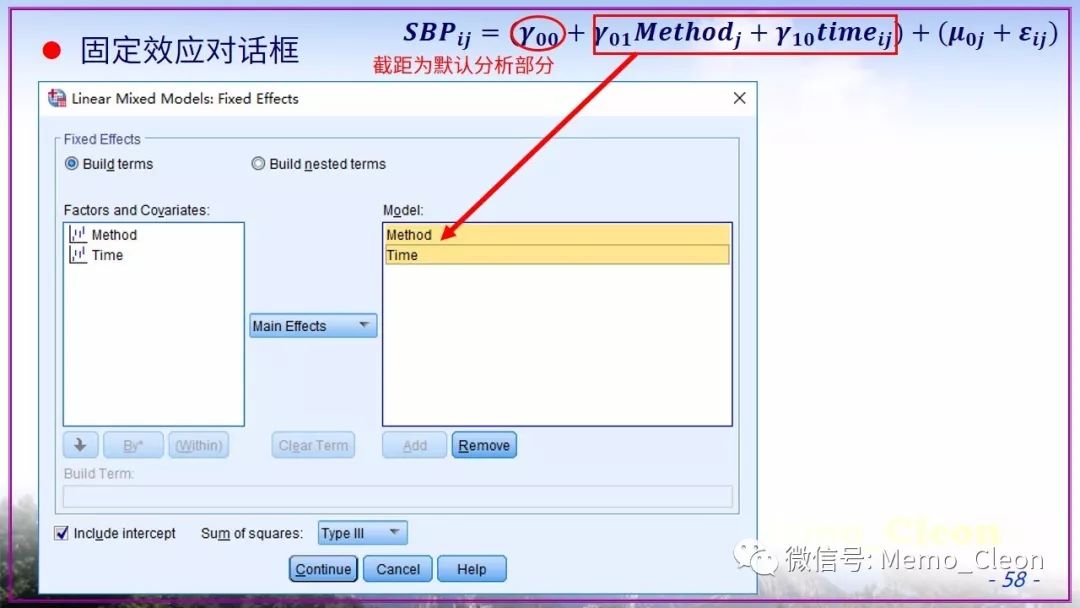
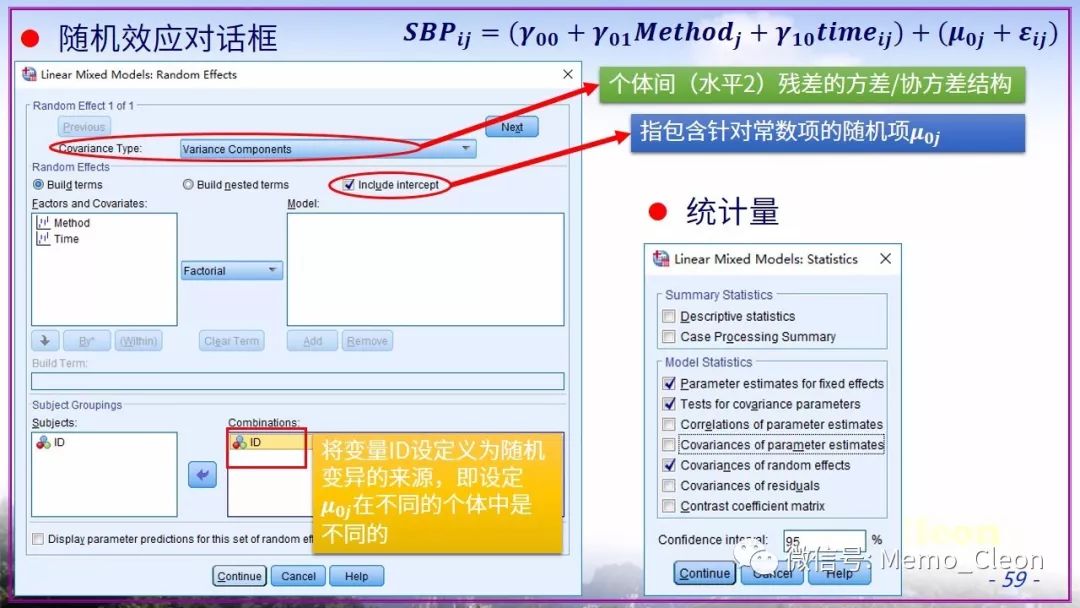
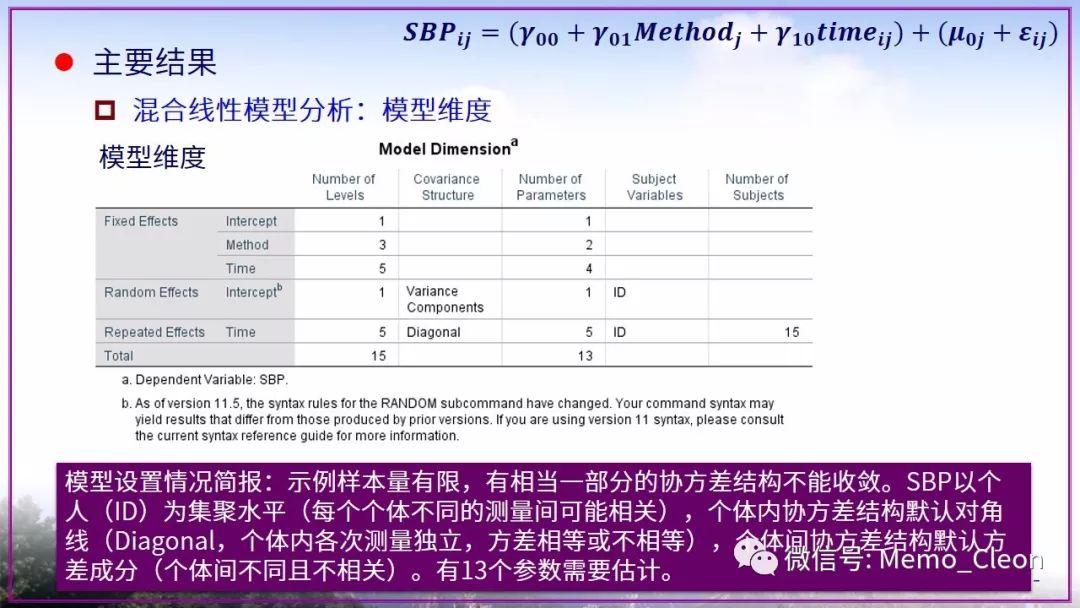
将懒进行到底……