
有序多分类的logistic回归在spss操作上并不难,难的是对回归系数的解释。诸多教程上将OR(即exp(β))解释为“固定其他因素的影响,自变量每改变一个单位,因变量提高至少一个(一个及一个以上)等级的优势比”,对于这个解释,我至今没弄明白是什么意思。个人理解,OR更为通俗的解释可以是“自变量某取值水平 更倾向因变量低赋值等级效应的可能性 是参照水平的多少倍”,如本笔记后面示例中“男性治疗效果差的可能性女性的3.74倍”。其中,因变量低赋值等级是指其value值较小的等级,但如果在广义线性模型或者利用程序改变了默认的分类顺序(Category order),此处的“低赋值等级”就应改为“低分类顺序”,另外正确理解“低赋值等级效应”很关键,是倾向有效呢还是无效,这是个关乎你结论是否正确的大是大非问题。
有序多分类资料的logistics回归使用的是累积logit回归模型,进行logit变换的是因变量有序取值水平的累积概率,实际上是将因变量按取值水平重新分割成两个等级(水平),然后对这两个水平进行二分类的logistic回归。
适用条件
(1)因变量一个且为有序多分类变量,自变量可以一个也可多个,定量、定性资料均可。
(2)自变量间无多重共线。多重共线需要剔除部分共线的自变量。
(3)满足比例优势假定。不管从因变量的哪个水平进行分割,自变量对logit模型的效应相同,即重新拟合的多个二分类logistic回归模型中各自变量的回归系数βi相等,这是累积logit回归模型拟合的前提条件。是否满足比例优势假定,需要进行平行性检验,一般用似然比检验,要求P>0.05。如满足条件,n个等级的因变量可拟合n-1条空间中的平行直线,各自变量回归系数相同,不同的只是常数项α。当平行不满足时,可尝试修改链接函数(可在ordinal过程中的选项按钮中进行选择);如改用链接函数依旧不平行,可改用无序多分类的logistic回归。
在开始SPSS示例前,为了更好地理解回归系数和OR,有必要从模型的原理进行一些必要的解释。
先回顾几个概念:
比数(Odds):或称比值,优势,是两个概率之比,是某结果出现的概率与不出现的概率之比:Odds=P/(1-P)。如果P1>P2,则会有Odds1=P1/(1-P1) >P2/(1-P2)=Odds2。
logit变换:取发生率P比数的自然对数,即logit(P)=ln(Odds)。概率大于等于0小于等于1,比数把概率转化到了正无穷大,logit变化则将概率变成了负无穷到正无穷。
比数比(OR):或称比值比,优势比,是两个比数之比,或者说概率之比的比:OR= Odds1/Odds2=[P1(1-P2)]/[P2(1-P1)]。阳性结果很小(小于0.05)或很大时(大约0.95)时,OR约等于相对危险度RR。另外如果OR>1,则Odds1/ Odds2>1,进一步可得P1>P2,即OR是否大于1可用于两种情况下发生率大小的比较。
因变量y是有n个等级水平的有序变量,进行有序logistic回归时可以产生n-1个二分类模型。第k个等级(k=1,2,…n)的阳性概率分别为πk,则有π1+π2+…πn=1。自变量x有m个,第i个自变量(i=1,2,…m)Xi系数为βi。不同的统计软件采用的累积logit回归模型有所不同,模型表达形式如下(自上而下分别为Model1-3):
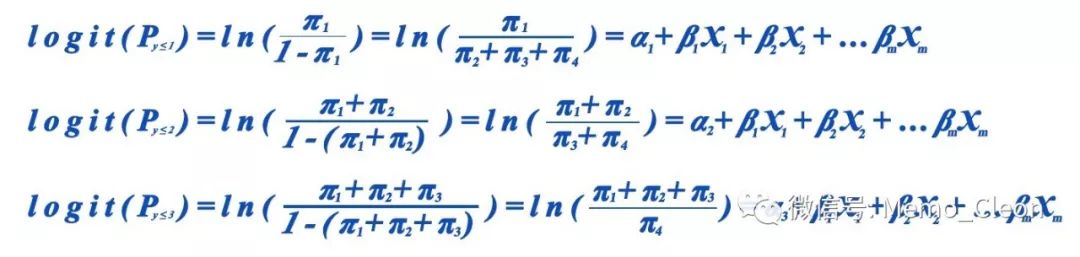
采用第1和第2个模型想要得出的结果是自变量对因变量某等级或更低赋值等级效应的影响,而第3个模型则是对某等级或更高赋值等级效应的影响。
不同的切割点有对应的常数项ak值(被称为截距intercept或阈值threshold),不同的模型可能会有差异,但累积logit模型要求各自变量对logit模型的效应相同(比例风险假定),即模型中各回归系数βi相等。由于自变量的参照水平不同,感兴趣的自变量对因变量效应不同,不同模型的得出的具体β值可能有差异,但在转成相同的表达方式后,效应应该是一致的。
SPSS采用的是第一个参数表达模型(Model 1)。假设因变量y有4个等级水平,相应概率则为π1、π2、π3、π4,则可以拟合3个logistic模型(Model1-3):
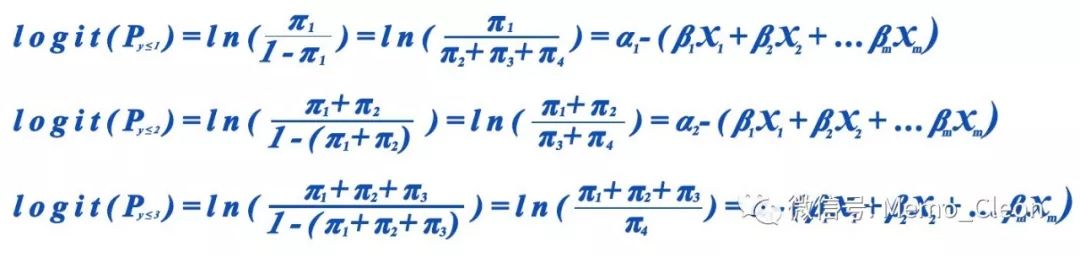
(1)二分类的logistic回归模型中logit(P)是某个水平概率比数的自然对数,而累积logit(P)是前n个等级(y≤n)概率之和(累积概率)的比数的自然对数,它没有固定的参考类别,是前n个等级(y≤n)的累积概率与前n个等级之后的所有等级(y>n)的累积概率之比的自然对数,更简洁地说就是前几个等级与后几个等级发生概率之比的自然对数。βi反应的就是自变量Xi每改变一个单位,前n个等级累积概率自然对数的变化,解释的是自变量X对前n个等级效应的大小。在实际操作中正确理解前n个等级的效应是很重要的,比如倾向低分等级还是高分等级,或者是倾向无效还是倾向有效。SPSS默认的前n个等级是对应value值较小的因变量,但如果改变默认的分类顺序(Category order),则对应分类顺序较小的因变量。OR=Exp(βi)就是前n个等级累积概率的比数比。另外a1<a2<a3。
(2)模型解释的SPSS官宣*1:
The parameter estimates table summarizes the effect of each predictor. While interpretation of the coefficients in this model is difficult due to the nature of the link function, the signs of the coefficients for covariates and relative values of the coefficients for factor levels can give important insights into the effects of the predictors in the model.
For covariates, positive (negative) coefficients indicate positive (inverse) relationships between predictors and outcome. An increasing value of a covariate with a positive coefficient corresponds to an increasing probability of being in one of the "higher" cumulative outcome categories.
For factors, a factor level with a greater coefficient indicates a greater probability of being in one of the "higher" cumulative outcome categories. The sign of a coefficient for a factor level is dependent upon that factor level's effect relative to the reference category.
SPSS给出的参数估计表格中,这种定性的描述有助于理解,总体来说同一个自变量的参数估计值(即β值)越大,对因变量的影响越倾向因变量高赋值效应(确切地说是高累积类别效应)【SPSS采用的Model1模型自变量回归系数前有符号“-”,自变量x赋值越小,logit(P)越大,因变量低赋值等级累积概率越大,高赋值等级累积概率越小。Model 1 incorporates a negative sign so that there is a direct correspondence between the slope and the ranking. Thus a positive coefficient indicates that as the value of the explanatory variable increases, the likelihood of a higher ranking increases*2】。
由于SPSS以较高赋值水平的自变量为参照水平(参照水平回归系数=0),与之相比,如果低赋值水平的自变量对应的是因变量低赋值等级的效应,那么回归系数就是负值;如果低赋值水平的自变量对应的是因变量高赋值等级的效应,回归系数就是正值。重要的事情需要不断的重复,正确理解低赋值和高赋值等级的效应非常重要。
除了这种定性的描述,我们还想得出OR,以定量的形式表达自变量每改变一个单位,低赋值等级累积概率与高赋值等级累积概率之比(Odds)是自变量变化前的多少倍,更容易理解的近似说法是:自变量某取值水平 更倾向因变量低赋值等级效应的可能性 是参照水平的多少倍。由于这种表述模式可能会出现小数倍,我们更习惯于表达方式是A是B的几分之一,或者B是A的几倍。因此实际应用时需要根据回归系数的正负值改成更符合语言习惯的表达形式:如果回归系数β为负,则表述为“自变量某取值水平 更倾向因变量低赋值等级效应的可能性 是参照水平的exp(-β)倍”;如果回归系数β为正,则表述为“自变量某取值水平 更倾向因变量高赋值等级效应的可能性 是参照水平的exp(β)倍”。重要的事情需要不断的重复,这里正确理解Odds的分子对应的效应非常重要。
示例数据来自孙振球主编的《医学统计学》第三版。某研究人员随机选择84例患某病的病人做临床试验,以探讨性别和治疗方法对该病疗效的影响,变量赋值为:性别(X1:男=0,女=1)、治疗方法(X2:传统疗法=0,新型疗法=1)、疗效(Y:无效=1,有效=2,痊愈=3)。请拟合性别、治疗方法对疗效的有序logistic回归模型。

SPSS操作及结果解读
1、数据录入
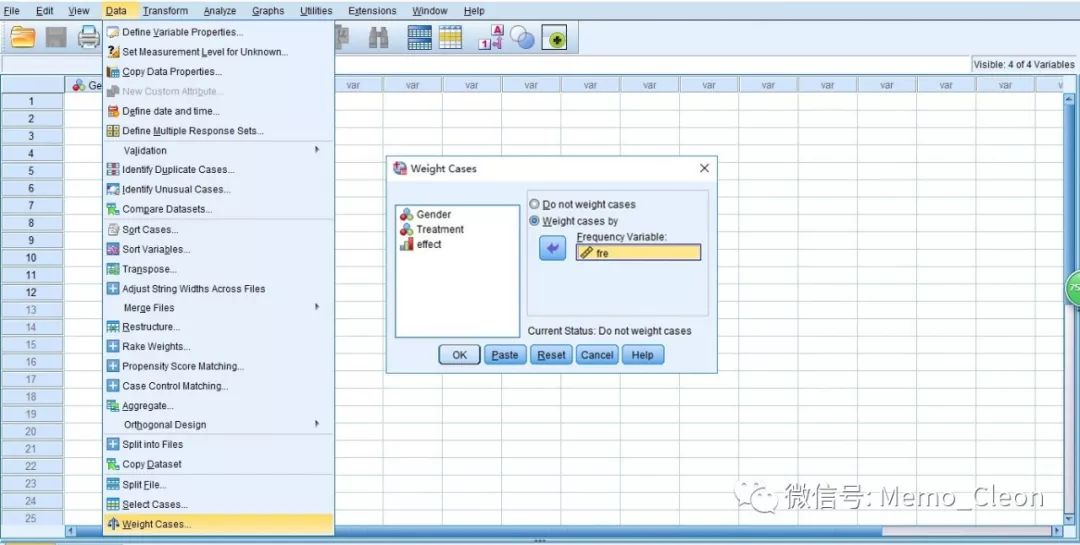
2、数据加权:Data>>Weight Cases…,将频数进行加权
3、有序回归分析:Analyze>>Regression>>Ordinal…
因变量(Dependent):effect;
因素(Factor):Gender、Treatment。因素可选入的是分类自变量,协变量(Covariate)选入连续性变量。
选项(Option…):较为重要的部分是链接函数的选择,默认是logit函数。
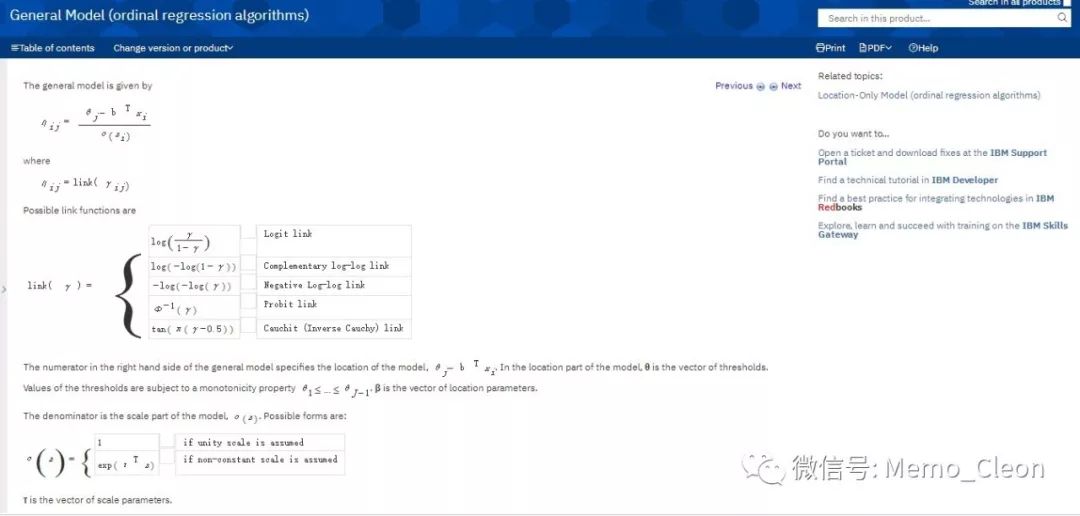
输出(Output…):默认选项有拟合优度检验(Goodness of fit statistics)、3个伪决定系数(Summary statistics)、参数估计(Parameter estimates)。其他还有参数估计的相关系数矩阵和协方差矩阵、单元格信息(实际频数、理论频数、残差)、平行性检验(Test of parallel lines),以及需要保存的变量(估计反应概率、预测分类、预测分类概率和实际概率),还有是否包含常数项。本例增选平行性检验。
Location…和Scale…用于分析交互作用时用到,一般默认选项即可
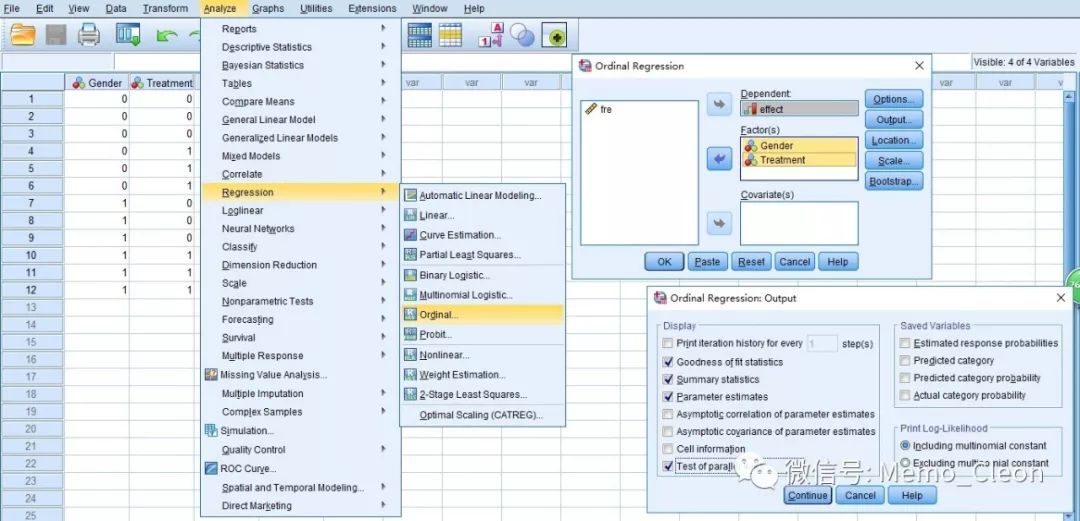
4、共线性检验:Analyze>>Regression>>Linear…
因变量(Dependent):effect;因素(Factor):Gender、Treatment。
选项(Option…):选中共线性诊断(Collinearity diagnostics)
5、结果与解读
结果首先给出一个警告信息:存在 1 (8.3%) 个频数为零的单元格(即通过合并预测变量值构成的因变量水平)。存在过多频数为0的单元格会影响模型拟合。单元格模式是自变量和因变量数值的组合,当自变量中有连续资料时,频数为0的单元格会比较多。
【1】个案处理概要。给出数据的基本信息

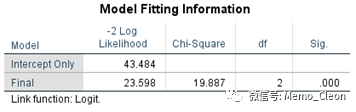
【2】模型拟合信息。假设检验H0假设是模型所有偏回归系数全部为0,采用的是最大似然比检验,只含常数项模型与最终模型的的负2倍最大似然比之差(-2 Log Likelihood值之差)为卡方值,χ2=43.484-23.598=19.887,P<0.001,说明至少有一个自变量的偏回归系数不为0。
【3】拟合优度检验。采用Pearson和Deviance两种方法,P均>0.05,拟合优度较好。但在频数为0的单元格较多时,这两个检验统计量结果将不可信。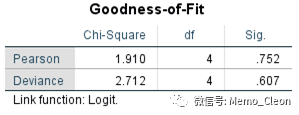
【4】伪R方。表示当前模型中自变量引起的因变量变异占因变量总变异的比例,对于分类数据的统计,R方一般都不会太高,意义不是太大。
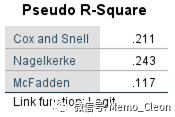
【5】参数估计结果。
这是有序多分类logistic回归中最重要的一张表格,输出了回归方程中的一些重要参数。阈值(threshold)表示的是常数项估计值,位置(location)则是用来估计偏回归系数。其他还有标准误、95%CI及估计值的wald检验结果。
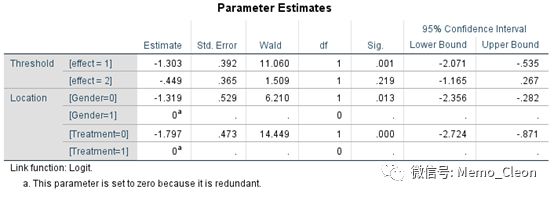
本例因变量3个等级,会得到两个回归方程:
logit(Py≤1)=ln(Py≤1/(1- Py≤1))
=-1.303-(-1.319·Gender-1.797·Treatment)
logit(Py≤2)=ln(Py≤2/(1- Py≤2))
=-0.449-(-1.319·Gender-1.797·Treatment)
即
logit(Py≤1)=ln(Py≤1/(1- Py≤1))
=-1.303+1.319·Gender+1.797·Treatment
logit(Py≤2)=ln(Py≤2/(1- Py≤2))
=-0.449+1.319·Gender+1.797·Treatment
注意最终回归方程中自变量系数β前还有符号“-”,参见文章开始介绍。
常数项有两个,effect=1代表无效概率/(有效+痊愈)累积概率模型的截距,effect=2代表(无效+有效)累积概率/痊愈概率模型的截距,且第二个累积概率方程的截距(-0.449)>第一个累积概率方程的截距(-1.303)。
有序多分类的logistic回归分析要求满足比例风险假定,各个回归方程的偏回归系数相同,因此结果中两个方程回归系数值只有一个。
总体而言,两个方程的分子累积概率更倾向于无效的效应,分母更倾向有效的效应,因此该模型分析的是因变量更倾向于无效的影响因素,而不是分析更倾向于有效的影响因素。
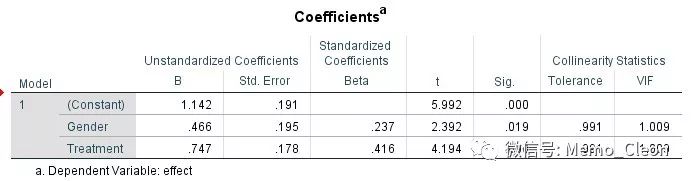
性别wald χ2=6.210,P=0.013<0.05,说明性别对疗效的影响有统计学差异。
估计值(回归系数β)为负,说明相比女性(自变量高水平),男性(自变量低水平)对倾向无效(低赋值等级效应)的影响更大,可以更通俗地表达为相比女性,男性的治疗效果更差。如前所言,同一个自变量的参数估计值(即β值)越大,相对应的因变量的效应是越倾向高赋值等级。如果自变量是二分类变量,估计值为正则说明高赋值等级效应更有可能是因为自变量第一个类别(第二个类别是参照水平),估计值负则说明低赋值等级效应更有可能是因为第一个类别;如果是协变量(连续变量),正值表示随着变量值的增加,对应 成为高赋值积累类别效应 的可能性也增加。
如果还想进一步知道差多少,就需要计算OR值。OR= exp(-(-1.319))=3.74,即男性治疗效果差的可能性是女性的3.74倍。此处需要两点:一是回归系数β估计值(即Parameter Estimates表中的估计值)的正负是相对于参照水平而言的;二是回归方程的偏回归系数β前有“-”号(见本文开始),本例两个自变量的偏回归系数均为负值,在最终的方程中变为正值。
当然,①男性治疗效果差的可能性女性的3.74倍,还可以用其他的形式表达,比如②男性治疗效果好的可能性为女性的exp(-1.319)=0.28倍;或者③女性治疗效果差的可能性为男性的exp(-1.319)=0.28倍;或者④女性治疗效果好的可能性为男性的exp(1.319)=3.74倍。由于语言习惯,我们倾向于表达A是B的几分之一或者多少倍。当估计值正时,最直接的解释是“自变量某取值水平更倾向因变量低赋值等级效应的可能性是参照水平的exp(-β)倍”,但此时exp(-β)倍为小数,不符合我们的语言习惯,可解释为“自变量某取值水平更倾向因变量高赋值等级效应的可能性是参照水平的exp(β)倍”;若估计值为负时,则表述为“自变量某取值水平更倾向因变量低赋值等级效应的可能性是参照水平的exp(-β)倍”。
同样,可以对治疗方法可做出解释:
治疗方法wald χ2=14.449,P<0.001,说明治疗对疗效的影响有统计学差异;相比新型疗法,传统疗法的治疗效果更差;传统疗法效果更差的可能性是新型疗法的exp(-(-1.797))=6.03倍。
SPSS的Ordinal过程并没有直接给出OR,自变量少时可以直接手工计算或者借助excel求出。自然对数底e=2.71828…,OR=e的β次方,Excel中可在表格中直接输入“=exp(β)”即得。当自变量较多时,可用广义线性模型(Generalized Linear Models)求得。
Analyze>>Generalized Linear Models >>Generalized Linear Models…
模型类型(Type of model):根据资料类型选择有序logistic(Ordinal logistic)
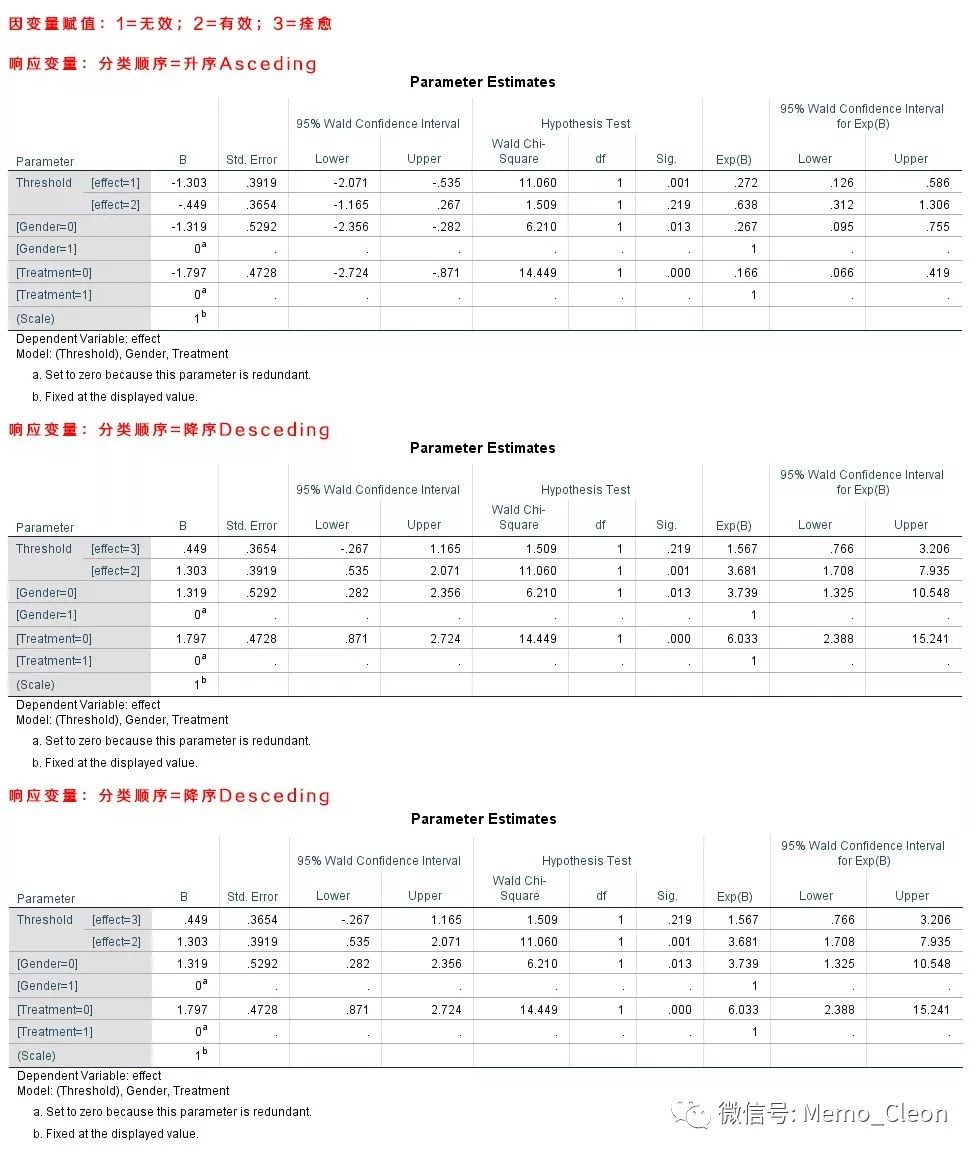
响应变量(Response):因变量选入effect。注意因变量分类顺序(Category order(Multinomial only))的选择,有Ascending、Descending和Data三个选项。升序(Ascending)为默认选项,表示按因变量赋值大小进行升序排列;降序(Descending)表示按因变量赋值大小进行降序排列,这样比数的分子就是赋值较大的因变量累积概率,对应的效应就与ascending恰好相反,结果的表述也需要反过来。
预测变量(Predictors):即自变量,将Gender和Treatment选入因素框
模型(Model):将Gender和Treatment按主效应(main effects)选入模型框
估计(Estimation):参数估计Parameter Estimation Method选择Fisher
统计(Statistics):除默认选项外,增加选项“包括指数参数估计值(Include exponential parameter estimates)”
其他按默认选项。结果如下:
响应变量分类顺序按升序排列同Ordinal过程结果,不做表述。
响应变量分类顺序按降序排列:按此顺序构建的两个回归方程,一个是代表痊愈概率/(有效+无效)累积概率,另外一个是(痊愈+有效)累积概率/无效的概率,分子倾向有效,分母更倾向无效,该模型分析的是因变量更倾向于有效的影响因素。
以自变量治疗方法为例,wald χ2=14.449,P<0.001,说明治疗对疗效的影响有统计学差异;相比新型疗法,传统疗法的治疗效果更差【回归系数β为正值,传统疗法更倾向分类高顺序类别效应,但此时的高顺序类别对应的是因变量的低赋值水平,即无效效应】;传统疗法效果更好(分类低顺序类别,对应高赋值水平的有效有效)的可能性是新型疗法的exp(-1.797)=0.166倍,更合乎习惯的表述是:传统疗法效果更差(高顺序类别,低赋值水平的无效效应的可能性是新型疗法的exp(1.797)=6.03倍。
【6】平行性检验。检验是否满足风险比例假定,即检验自变量对因变量的影响在各个回归方程中是否相等(各自变量系数在各个模型中是否相等)。似然比χ2=1.469,P=0.480>0.05,满足平行性的假设。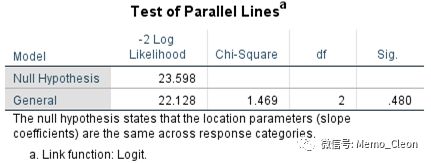
【7】共线性检验结果。容忍度(Tolerance)<0.1,方程膨胀因子(VIF)>10,提示共线性的存在。本例检验结果提示不存在共线性,可以进行有序多分类的logistic回归。
*1:SPSS Statistics 25.0.0 Interpreting the Model Interpreting the Model
*2:Ordinal Logistic Regression Models and Statistical Software: What You Need to Know
END


