统计方法一般都有其适用的条件,或者说是必须满足的统计假设。使用线性回归需要满足线性、独立性、正态性、方差齐性、自变量间不存在多重共线、因变量为连续变量。不考虑前提条件地生搬硬套,也不对模型进行诊断,只能是“Garbage in,garbage out”。今天谈谈线性回归的正态性检验的方法论。
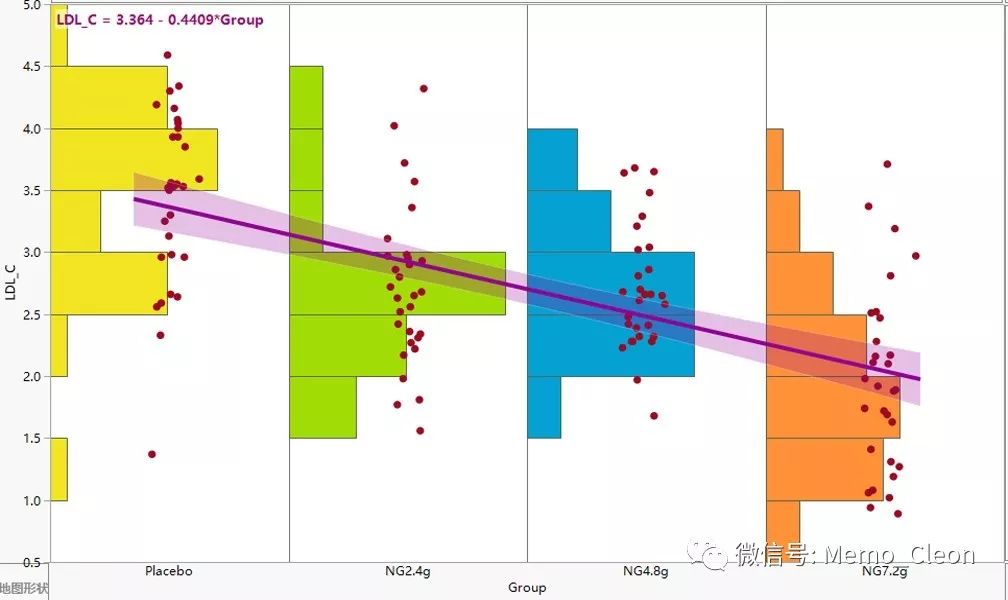
今天我们重点讨论的是第二种情况:当自变量为连续变量时。此时自变量每个“水平”的取值往往只有有限几个甚至只有1个,其对应的因变量观测值也只有几个甚至1个,毕竟每个自变量一次抽样只能对应一个因变量值,很显然这么小的样本量没法直接像自变量为分类变量那样考察每个“水平”的因变量值是否正态。而且连续性变量取值往往较多,即使我们的样本量足够大,自变量的每一个固定值有多个取值,这种考察正态性的工作量也会变的很大。这种情况下,对正态性的考察回归到对所有残差的考察反而更简便。
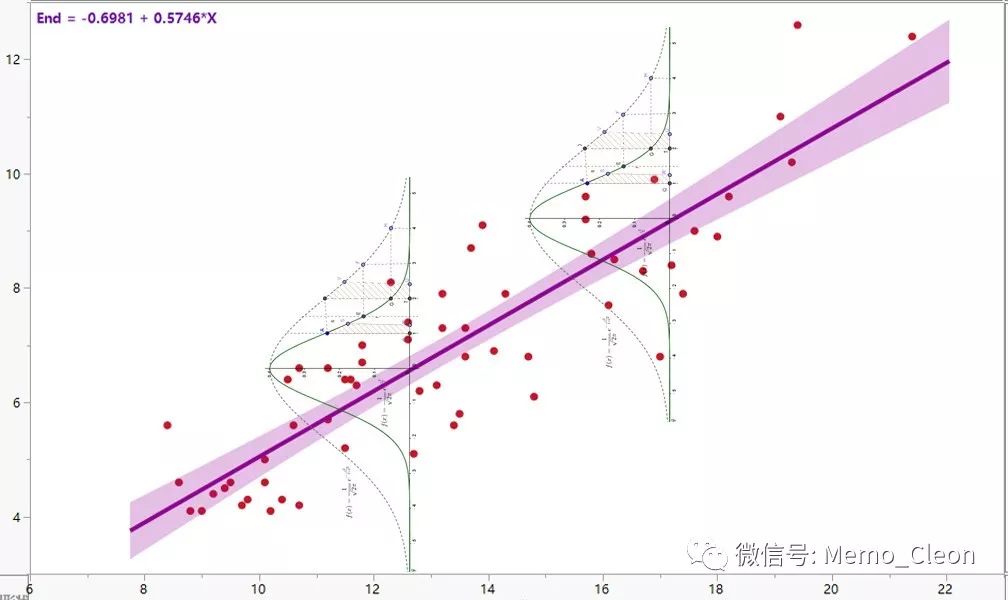

这是一个简单线性回归,回归方程并不难求:
Analyze>>Regression>>Linear……
Dependent(因变量):选入Uc;
Independent(自变量):选入age;变量筛选方法(Method)选择ENTER;
Statistics…:除默认的回归系数估计、模型拟合检验外,选中R2改变量;
Plots…:Y选入*ZRESID(标准化残差),X选入*ZPRED(标准化预测值),选中Histogram(标准化残差的直方图)、Normal probability plot(标准化残差的正态概率图)复选框;
Save…:非标准化预测值、标准化预测值、非标准化残差、标准化残差。
模型概要:纳入年龄变量,对模型的改变是有统计学意义的(P=0.004);相关系数R为0.882表明年龄与尿肌酐的回归关系较为密切;决定系数R2为0.778,表明年龄可以解释的变异占总变异的77.8%,即年龄可解释因变量77.8%的变异;校正的决定系数R2主要用于多重线性回归时不同数量的自变量模型间的拟合效果比较,简单线性回归中无实际意义。
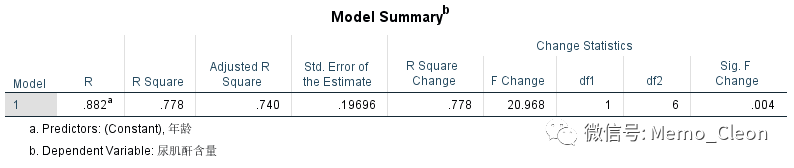
回归模型方差分析检验:F=20.968,P=0.004<0.05,表明纳入自变量的回归系数不全为0,回归模型有统计学意义。由于本例是只有一个自变量的简单线性回归,其等价于年龄的回归系数具有统计学意义。
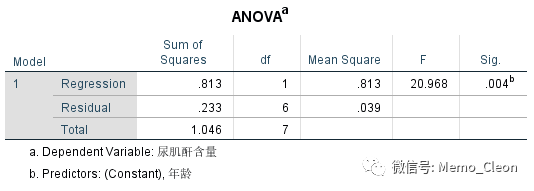
回归系数:Uc=0.139*age+1.662,年龄每增加1岁,尿肌酐含量平均升高0.139mmol/24h。常数项和年龄的系数的t检验表明两者均有统计学意义(两者都不为0)。注意年龄系数检验统计量t=4.579恰好为模型方差检验统计量F的平方根。
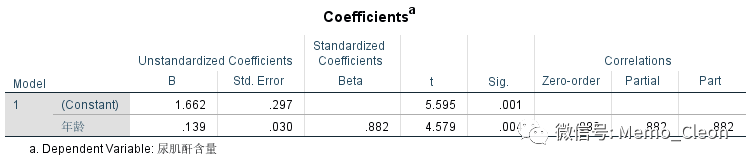
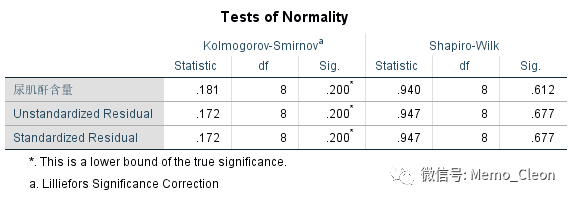
【1】图示法:如直方图、Q-Q图、P-P图等。直方图和Q-Q图在上述的线性回归操作中会自动生成,P-P图、Q-Q图也可在菜单生成(分析>>描述性统计量>>P-P图;分析>>描述性统计量>>Q-Q图)。从直方图和P-P上看,残差基本满足正态分布。
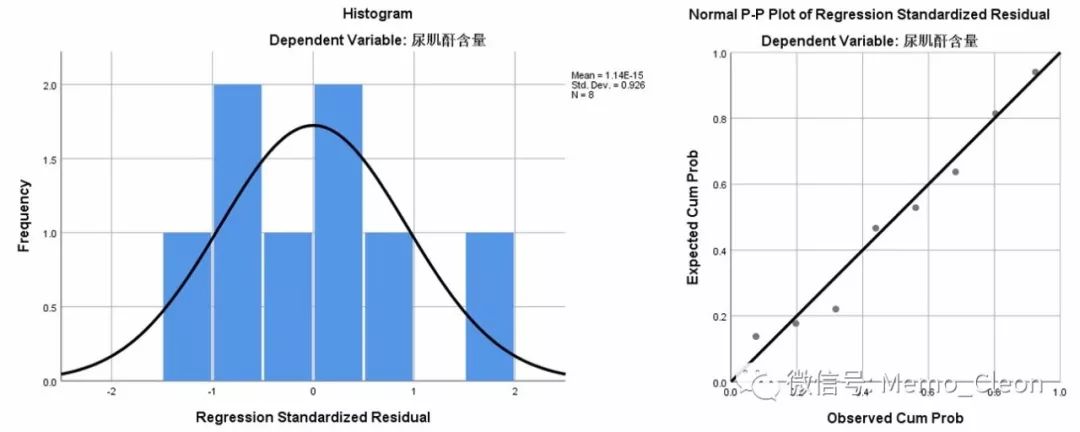
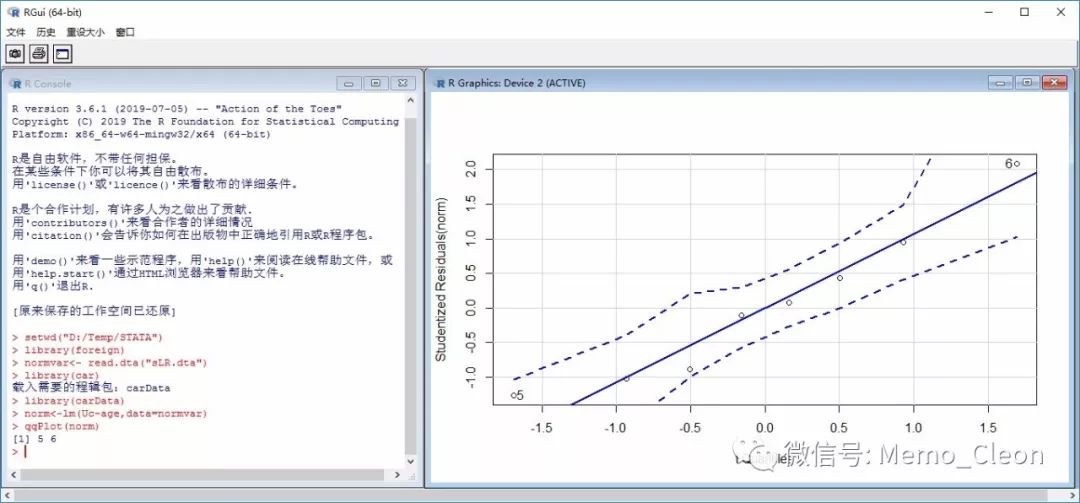
附R命令语句清单
setwd("D:/Temp") #设置工作目录#
library(foreign) #加载foreign程序包#
normvar<- read.dta("sLR.dta") #从STATA中导入数据#
norm<-lm(Uc~age,data=normvar) #以age拟合Uc的直线回归#
library(car) #加载car程序包#
library(carData) #加载carData程序包#
qqPlot(norm) #Q-Q图#
JMP 操作步骤:
分析>>以X拟合Y;
l Y,响应:Uc,X,因子:age,确定;
l 二元拟合,以“age”拟合“Uc”前倒三角菜单>>拟合线;
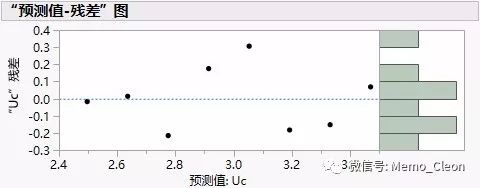
l 线性拟合前倒三角菜单>>保存残差,保存预测值,标绘残差;
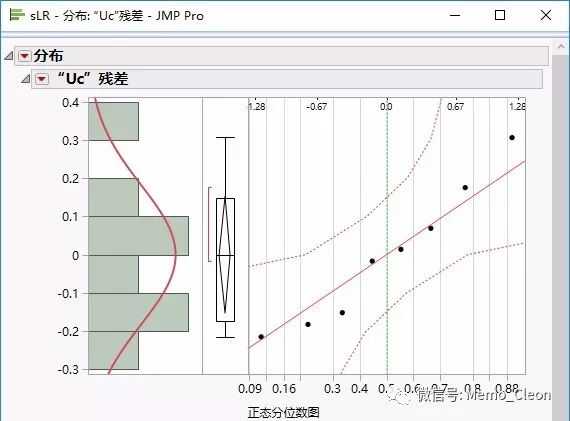
分析>>分布;Y,列:“Uc”残差;确定;
l “Uc”残差前倒三角菜单>>正态分位数图;
l “Uc”残差前倒三角菜单>>连续拟合>>正态。
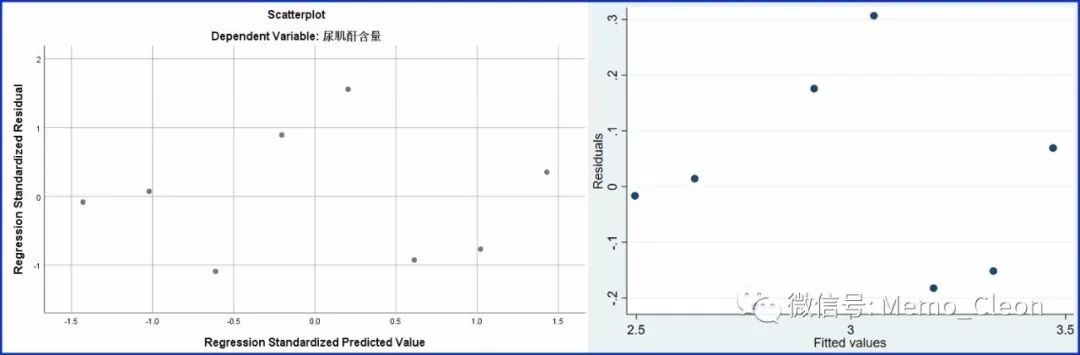
左上图按上述SPSS操作可以直接生成;
右上图STATA步骤:
统计>>线性模型及相关>>线性回归:[模型]选项卡中因变量选择Uc,自变量选择age,确定;
统计>>线性模型及相关>>回归诊断>>残差对拟合值图,[主要]选项卡中直接点击的确定。
相应的STATA语句命令
use "D:TempsLR.dta"
regress Uc age
rvfplot