方差齐性,或者叫等方差性、同方差性,字面意思就是两组或多组的方差在统计学上相等,在方差分析或t检验中,取值相同的自变量水平有很多,因变量有充足的信息对方差进行分析。但在直线回归中,每个自变量“水平”的取值往往只有有限几个甚至只有1个,每个自变量一次抽样只能对应一个因变量,其对应的因变量观测值也只有几个甚至1个,每个“水平”的方差可能都没法计算,何来方差齐性呢?而且即使我们的样本量足够大,自变量的每一个“水平”多个取值,但由于自变量有太多的“水平”使得这种考察变得很艰难。线性回归中的等方差指因变量残差不随所有自变量取值水平的变化而变化,其检验实际上只是对因变量残差的一种探察。在自变量与残差或预测值和残差的散点图上,标准化残差随机、均匀的散布在0横线上下两侧,即不论自变量或因变量的预测值如何变化,标准化残差的波动基本保持稳定,可认为方差基本相等,但如果标准残差自变量或预测值增大出现扩散或收敛,则方差可能不齐。当然如果你觉得图示法太主观而不敢下结论,也可以改用统计学检验的方法。
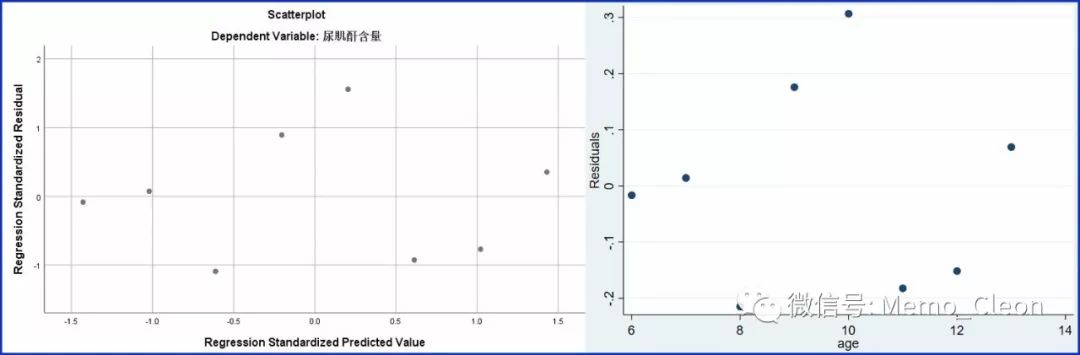
左上图为标准化预测值与标准化残差的散点图,在线性回归的SPSS操作可以直接生成,可参见[线性回归中的正态分布];
右上图为自变量与残差的散点图,STATA步骤如下,注意在模型诊断前首先要进行线性回归:
统计>>线性模型及相关>>线性回归:[模型]选项卡中因变量选择Uc,自变量选择age,确定;
统计>>线性模型及相关>>回归诊断>>残差对预测值图,[主要]选项卡中自变量下拉框中选择age,确定。
相应的语句命令如下
use "D:TempsLR.dta"
regress Uc age
rvpplot age
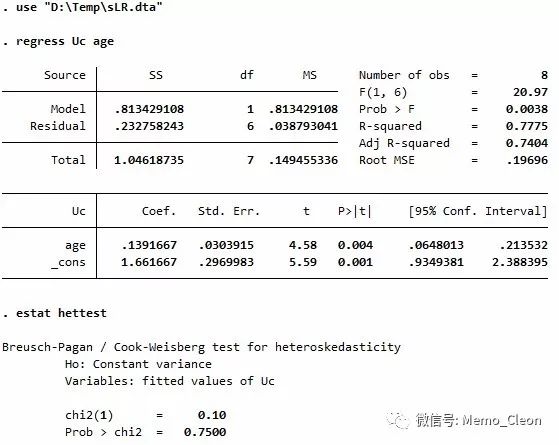
STATA检验步骤:统计>>线性模型及相关>>回归诊断>>模型检定等。
默认就是异方差检验,有3种检验类型(方法)可供选择,以及检验使用的变量(默认采用回归拟合值)。注意在模型诊断前首先要进行线性回归。结果提示,在0.05的检验水准上并不能拒绝“方差相等”的假设(P=0.75>0.05),即可认为方差相等。
estat hettest performs three versions of the Breusch-Pagan (1979) and Cook-Weisberg (1983) test for heteroskedasticity. All three versions of this test present evidence against the null hypothesis that t=0 in Var(e)=sigma^2 exp(zt). In the normal version, performed by default, the null hypothesis also includes the assumption that the regression disturbances are independent-normal draws with variance sigma^2. The normality assumption is dropped from the null hypothesis in the iid and fstat versions, which respectively produce the score and F tests discussed in Methods and formulas in [R] regress postestimation. If varlist is not specified, the fitted values are used for z. If varlist or the rhs option is specified, the variables specified are used for z.
setwd("D:/Temp") #设置工作目录#
library(foreign) #加载foreign程序包#
normvar<- read.dta("sLR.dta") #从STATA中导入数据#
var<-lm(Uc~age,data=normvar) #以age拟合Uc的直线回归#
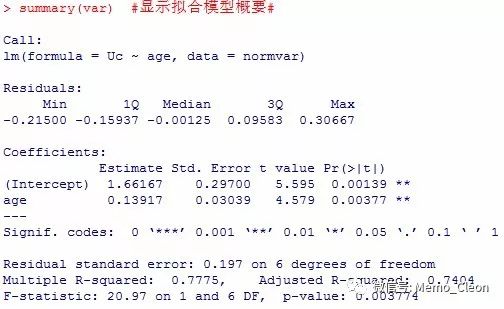
summary(var) #显示拟合模型的详细结果①#
library(zoo) #加载zoo程序包#
bptest(var) #Breusch-Pagan检验②#
library(carData) #加载carData程序包#
ncvTest(var) #得分检验残差是否恒定③#
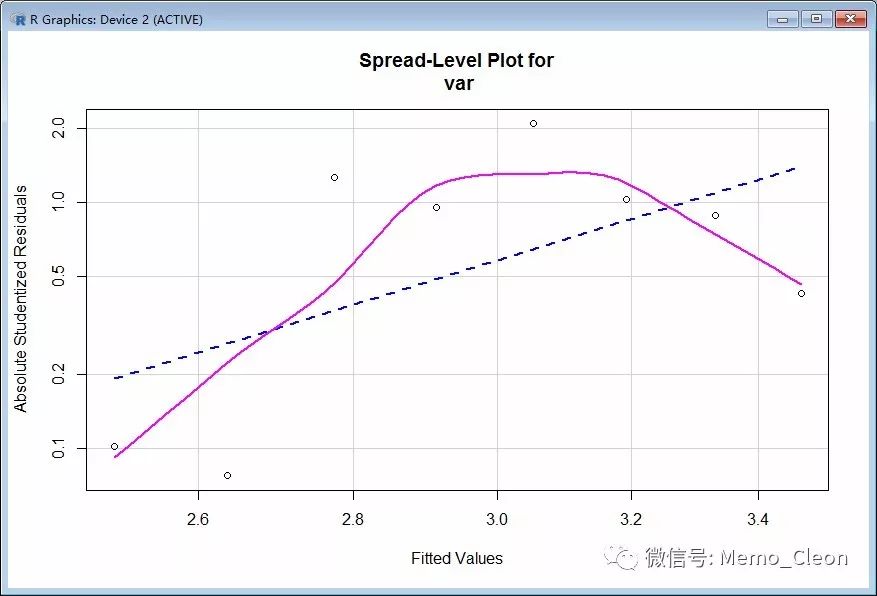
spreadLevelPlot(var) #分散水平检验,创建含有最佳拟合曲线的拟合值与标准残差绝对值的散点图④#
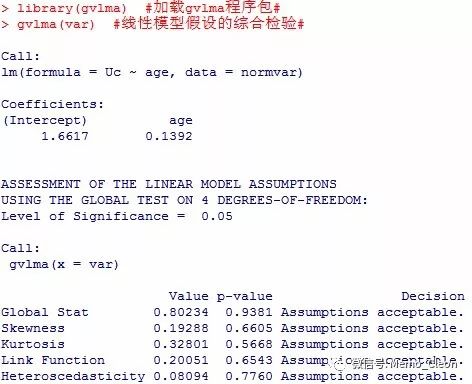
gvlma(var) #线性模型假设的综合检验⑤#
studentized Breusch-Pagan test
data: var
BP = 0.20142, df = 1, p-value = 0.6536
③得分检验(ncvTest)结果:P=0.7500>0.05,残差不随拟合值的变化而变化,即残差保持恒定。
Non-constant Variance Score Test
Variance formula: ~ fitted.values
Chisquare = 0.1015182, Df = 1, p = 0.75002
Suggested power transformation: -5.02297