马克思说联系是普遍的,世界上一切事物都处于普遍联系之中!相关就是联系的一种。谈到相关,肯定是至少两个变量间的关系,一个变量是无所谓相关的。根据两个变量的类型不同,在考察相关时用到的相关指标也会不同。一般相关系数在0~1或者-1~1之间,绝对值越大,相关性越强,如有正负号,正负号仅代表相关的方向。
【1】相关:Analyze>>Correlate>>Bivariate…
【2】交叉表统计量:Analyze>>Descriptive Statistics>>Crosstabs…
[Statistics…]按钮打开对话框如下
【3】线性回归:Analyze>>Regression>>Linear…
[Statistics…]按钮:选中Covariance matrix可获得自变量间的相关系数。选中Part and partial correlations可获得0介相关、部分相关和偏相关,自变量与因变量的0介相关是等同两者的Pearson相关。

【1】数据录入:共三个变量:id,age,Uc,具体略。
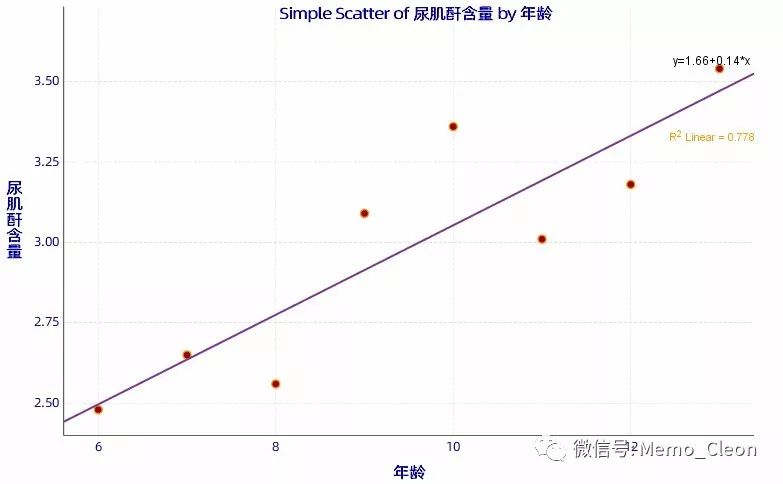
【3】双变量正态分布:SPSS中并未给出多元正态分布的检验方法,可采用STATA或者R进行检验,可参考文章《多元正态分布的检验》、《多元正态分布检验的R实现方法》。
以R为例,采用mshapiro.test {mvnormtest}命令代码如下:
library(foreign) #调用程序包foreign
tv<-read.spss(file="D:/Temp/STATA/sLR.sav",to.data.frame = TRUE) #新建对象tv,并从从SPSS文件中读入数据
slr<-t(tv[2:3]) #新建对象slv,赋值是数据框tv第2-3列的转置后数据
library(mvnormtest) #调用程序包mvnnormtest
mshapiro.test(slr) #使用函数mshapiro.test对slr进行多元正态分布的检验
结果显示:W = 0.96215, p-value = 0.8303,数据呈多元正态分布。
将年龄和尿肌酐含量选入因变量框,[Plot…]选中带检验的正态分布图。
结果显示,不论KS还是SW检验,两个变量P均>0.05,数据均成正态分布。
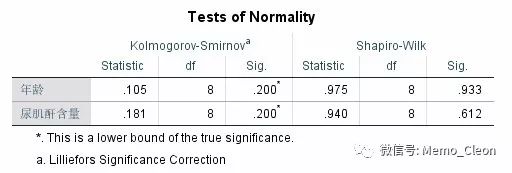
【4】简单相关分析:Analyze>>Correlate>>Bivariate…
将要分析的变量肺活量和胸围选入变量窗口;
相关系数默认是Pearson,我们同时选中Spearman;
默认双尾检验和标注显著的相关;
[Options…]中选中均值和标准差、离均差交叉乘积和协方差。
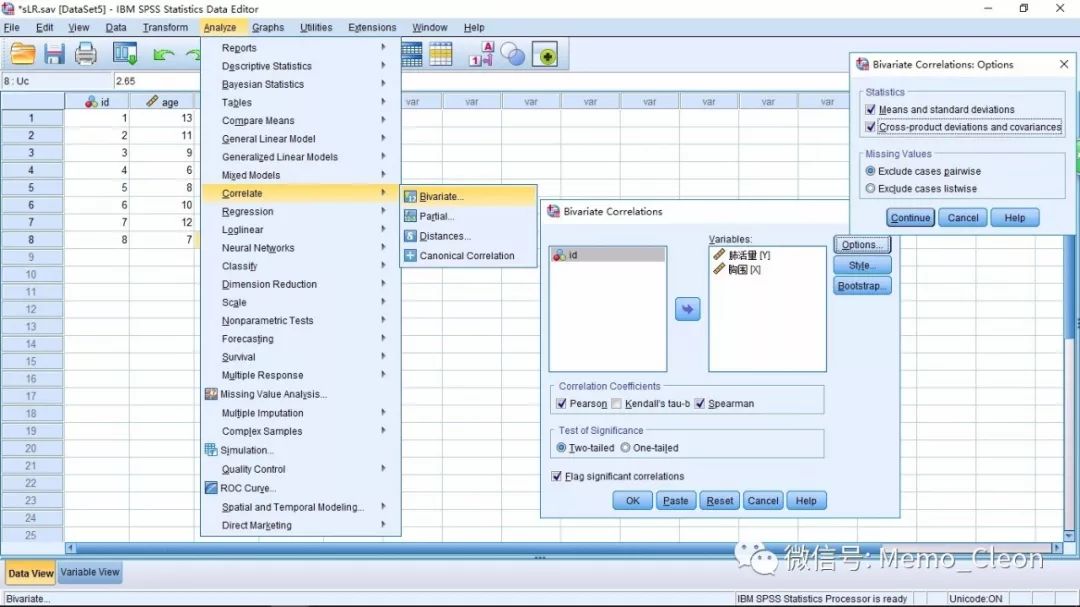
【5】结果:
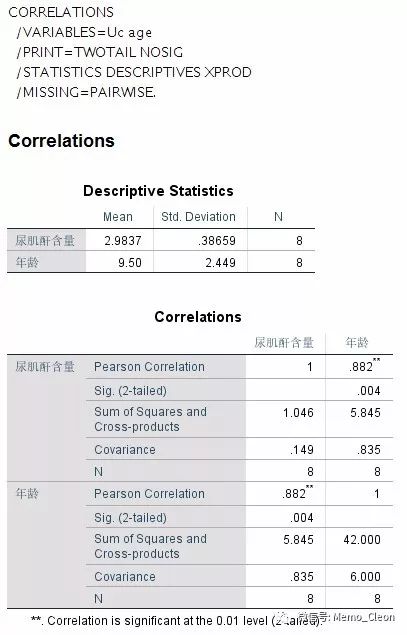
结果首先给出了尿肌酐和年龄的均数、标准差及案例数。
相关分析显示,尿肌酐含量和年龄积差相关系数(即Pearson相关系数)是0.882,P=0.004<0.05,可以认为尿肌酐含量和年龄的正相关关系是有统计学意义的,即随着年龄的增长尿肌酐含量也会越来越高。同时结果中也给出了离均差平方和或者交叉乘积和以及协方差。关于离均差平方和协方差的理解可参见文末。
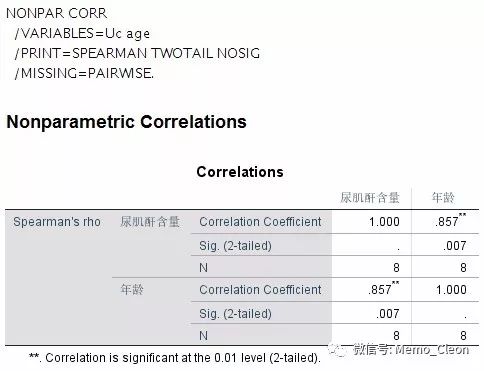
Spearman相关系数也叫秩相关系数,属于非参数检验的方法,当Pearson的适用条件不满足时可以采用该系数,但跟其他非参检验一样,相比参数检验其检验效能会低一些。本例Spearman相关系数=0.857,P=0.007<0.05。

补充说明:离均差平方和、协方差

协方差跟方差实际上是一回事,方差反应的是某个变量的离散水平,协方差反应的是两个变量间的离散水平。

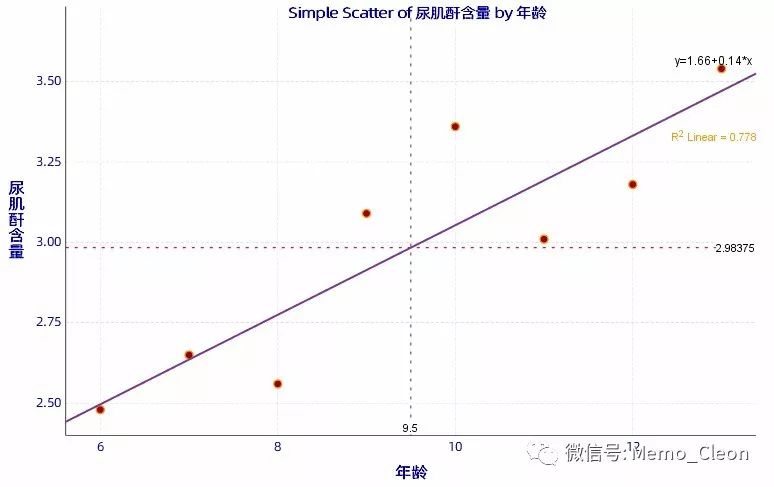
最后看一下本例Pearson相关系数结果:Uc的标准差=0.38659,年龄标准差=2.449,Sum of Squares and Cross-products是离均差的平方和或者交叉乘积和,Uc与age的交叉乘积和=5.845,Uc的离均差平方和=1.046,age的离均差平方和=42。离均差平方和除以n-1的结果的正平方根即是相应的标准差,如1.046/(8-1)=0.386592。


