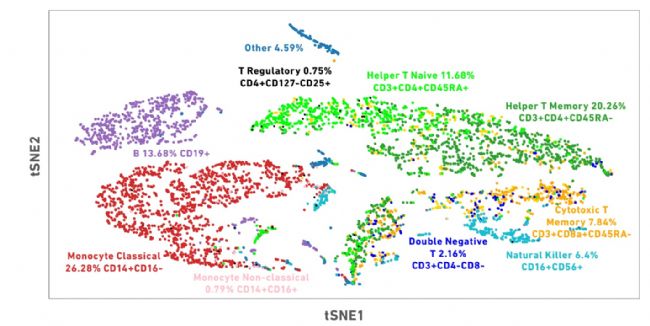
高通量单细胞组学数据的一个显著性特点就是数据量大,一次能反映的细胞数量多。因此,通过降维和可视化去展示细胞数据特征是一个非常重要的工作。翻开各类发表的单细胞组学文章,不管是CNS的还是其他,几乎所有的结果中,映入眼帘的第一张图片通常是数据结果的降维图形化展示。
对高维单细胞数据的可视化展示,以t-SNE为代表的非线性降维技术,由于其能够避免集群表示的过度拥挤,在重叠区域上能表示出不同的集群而被广泛运用。然而,任何技术方法都不是完美的,t-SNE也一样,它的局限性体现在丢失大规模信息(集群间关系)、计算时间较慢以及无法有效地表示非常大的数据集[6]等方面。
那么,有没有其它方法能在一定程度上克服这些弱点呢?
UMAP就是这样一个能解决这些问题的降维和可视化的工具。
统一流形逼近与投影(UMAP,Uniform Manifold Approximation and Projection)是一种新的降维流形学习技术。UMAP是建立在黎曼几何和代数拓扑理论框架上的。UMAP是一种非常有效的可视化和可伸缩降维算法。在可视化质量方面,UMAP算法与t-SNE具有竞争优势,但是它保留了更多全局结构、具有优越的运行性能、更好的可扩展性。此外,UMAP对嵌入维数没有计算限制,这使得它可以作为机器学习的通用维数约简技术。
从上述定义可以看到,UMAP对于单细胞这类大数据、高维数据来说,是一个正中下怀的好工具。那么,在真实数据运用中,这种优势能体现出来吗?以下我们通过实际数据对比进行展示。
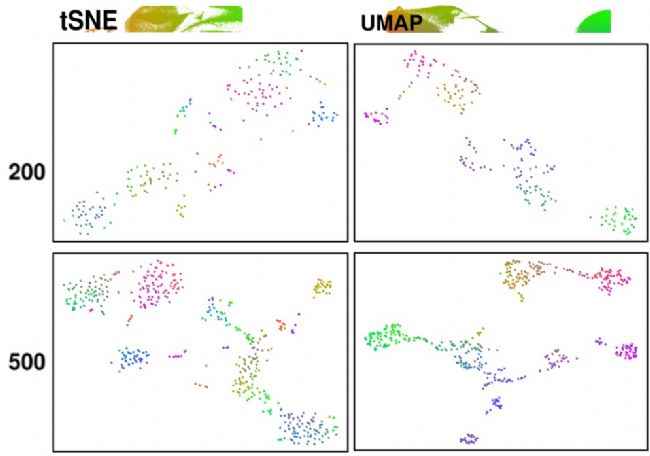
1.小数据集中,t-SNE和UMAP差别不是很大
我们分别以个和个单细胞的转录组数据为基础,分别通过和进行降维可视化展示,得到如下图:
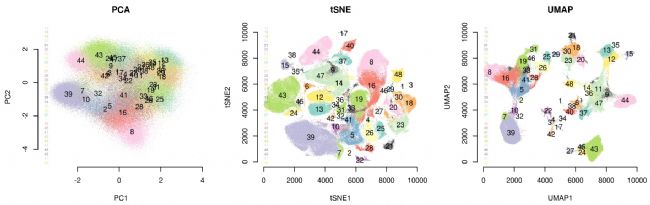
2.大数据集中,UMAP优势明显(30多万个细胞的降维可视化分析)
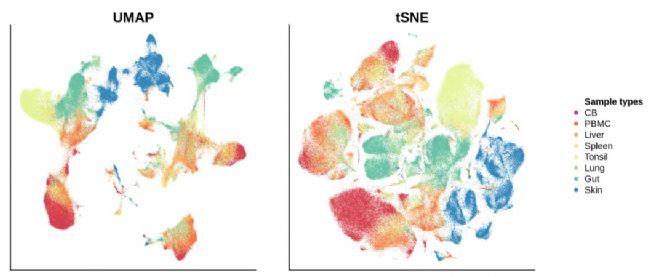
我们同时在一个数据集上运行、和,该数据集涵盖了来自个不同的富含和自然杀伤细胞的人体组织的个样本,共含有万多个细胞。
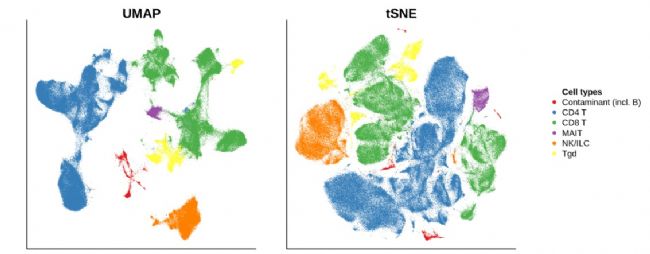
接下来,我们对上述数据分别用细胞类型和组织来源类型进行着色展示:
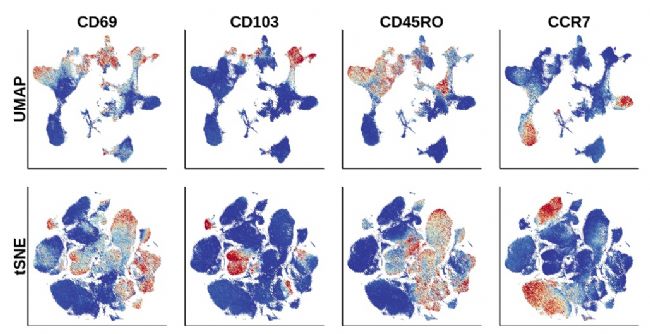
当我们对特定T细胞标志性marker进行绘图,我们观察到UMAP能够概括T细胞内每个主要集群的分化阶段,从UMAP投影上的驻留记忆T细胞标志物CD69和CD103、记忆T细胞标记CD45RO和幼稚T细胞标记CCR7的表达水平可见。相比之下,虽然t-SNE在群集中确定了类似的连续性,但它们沿共同轴没有明显的结构。
由此可见,在大数据降维和可视化方面优势突出。
参考文献:
[2] J. B. Kruskal. Multidimensional scaling by optimizing goodness of fit to anonmetric hypothesis. Psychometrika, 29(1):1–27, Mar 1964.
[3] Laurens van der Maaten and Geo‚rey Hinton. Visualizing data using t-sne.Journal of machine learning research, 9(Nov):2579–2605, 2008.
[4] Laurens van der Maaten. Accelerating t-sne using tree-based algorithms. Journal of machine learning research, 15(1):3221–3245, 2014.
[5] Ronald R Coifman and Stephane Lafon. Diffusion maps. Applied and computational harmonic analysis, 21(1):5–30, 2006.
[6]. Van Der Maaten, L. & Hinton, G. Visualizing high-dimensional data using t-SNE.journal of machine learning research. J. Mach. Learn. Res. 9, 26 (2008).
[7]. McInnes, L. & Healy, J. UMAP: uniform manifold approximation and projection for dimension reduction. Preprint at https://arxiv.org/abs/1802.03426 (2018).