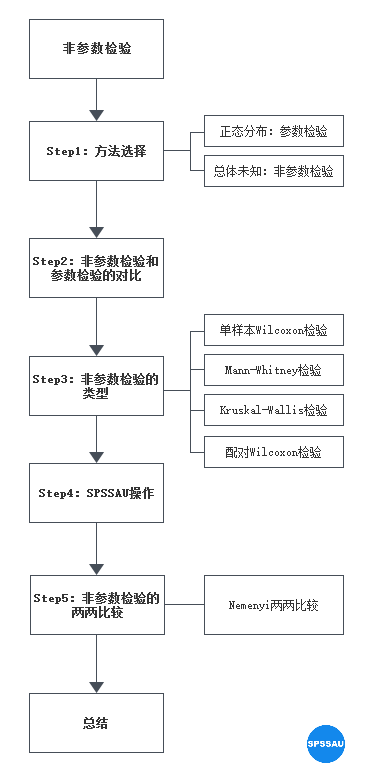
1. 何时使用非参数检验
或许你还没有理解什么是参数检验、非参数检验,但一定曾在无意之中使用过它们。如我们常用的方差分析、T检验,都属于参数检验。
参数检验,就是假定数据服从某种分布,通过样本信息对总体参数进行检验。因而在分析前,先要检验数据是否符合该类型的分布,如果数据无法满足检验假设的情况不符合分布情况,则可以考虑选择使用非参数检验。
比如,使用方差分析时,需要在分析前对数据的正态性和方差齐性进行判断,如果服从正态性、方差齐性,才可以使用方差分析。反之,如果没有满足这些假设条件,则考虑使用非参数检验。
2. 非参数检验和参数检验的对比
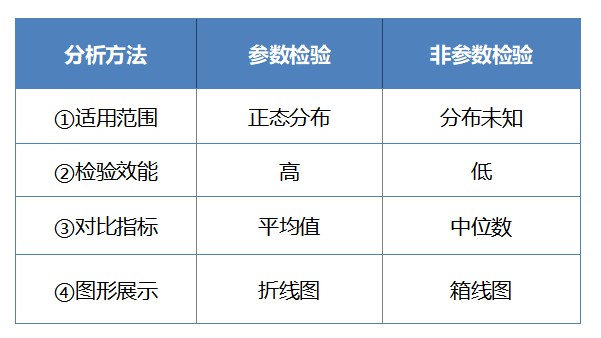
① 适用范围:
非参数检验用作参数检验的替代方法,当数据不满足正态性时,将使用非参数检验。因此,关键是要弄清楚是否具有正态分布。如果数据大致呈现"钟型"分布,则可以使用参数检验。
② 检验效能:
如果数据满足参数分布,应该优先选择参数检验方法。愿因在于参数检验的检验效能要高于非参数检验。尤其是在样本数较大的情况下,参数检验结果较为稳健,所以即使不服从正态分布,也会选择参数检验。
③ 对比指标:
参数检验一般用平均值反映数据的集中趋势;但由于数据不满足正态分布,在非参数检验中如果再使用平均值描述显然不太准确(比如常被吐槽的人均收入),此时中位数是更好的选择。
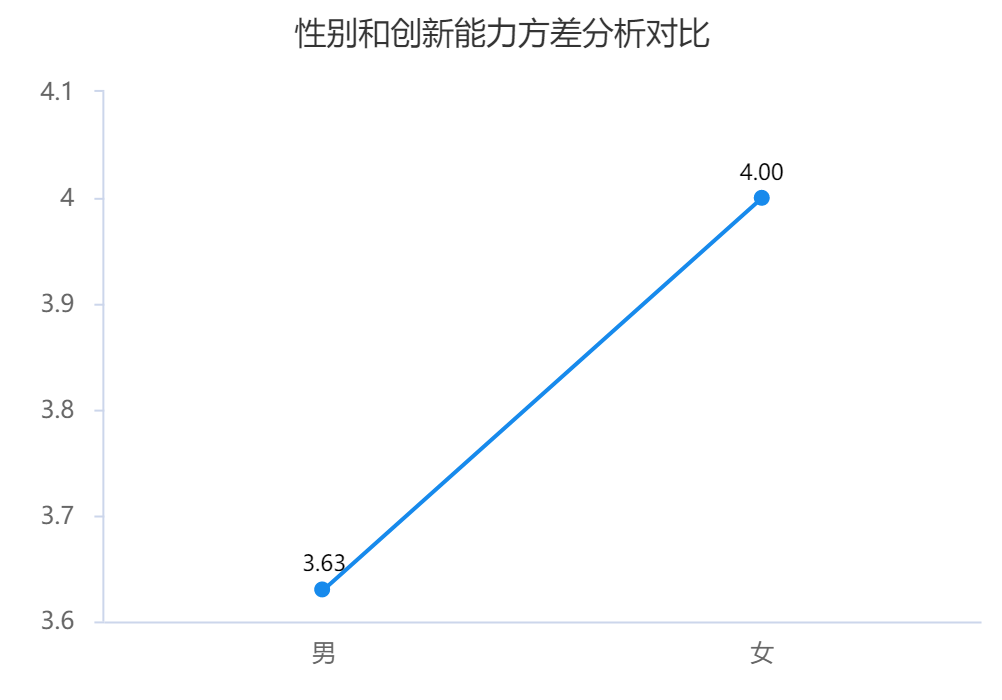
参数检验分析结果
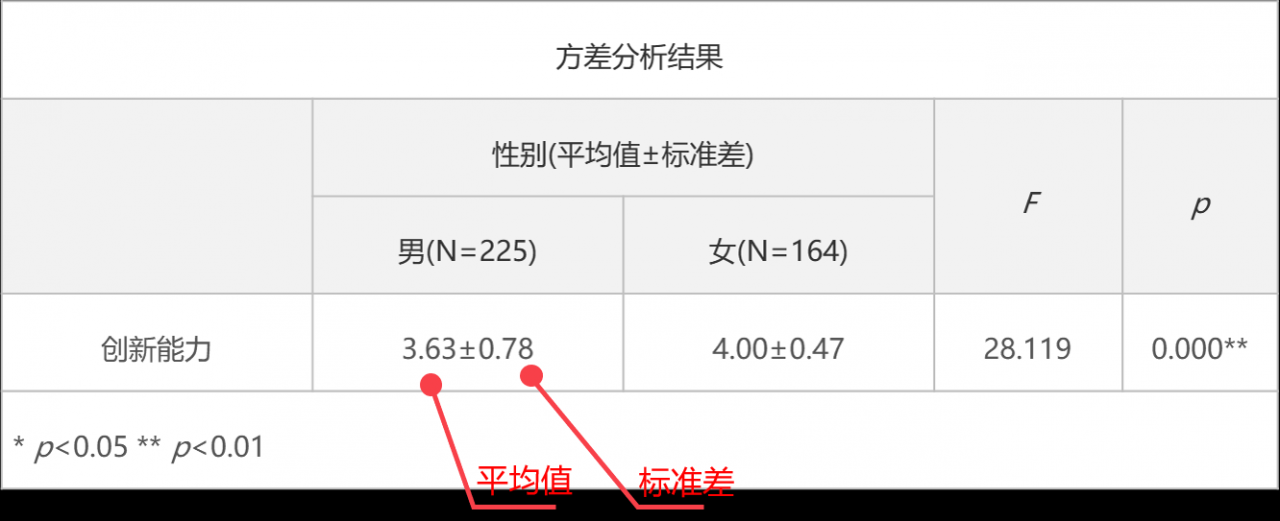
参数检验用平均值及标准差描述数据分布请况。
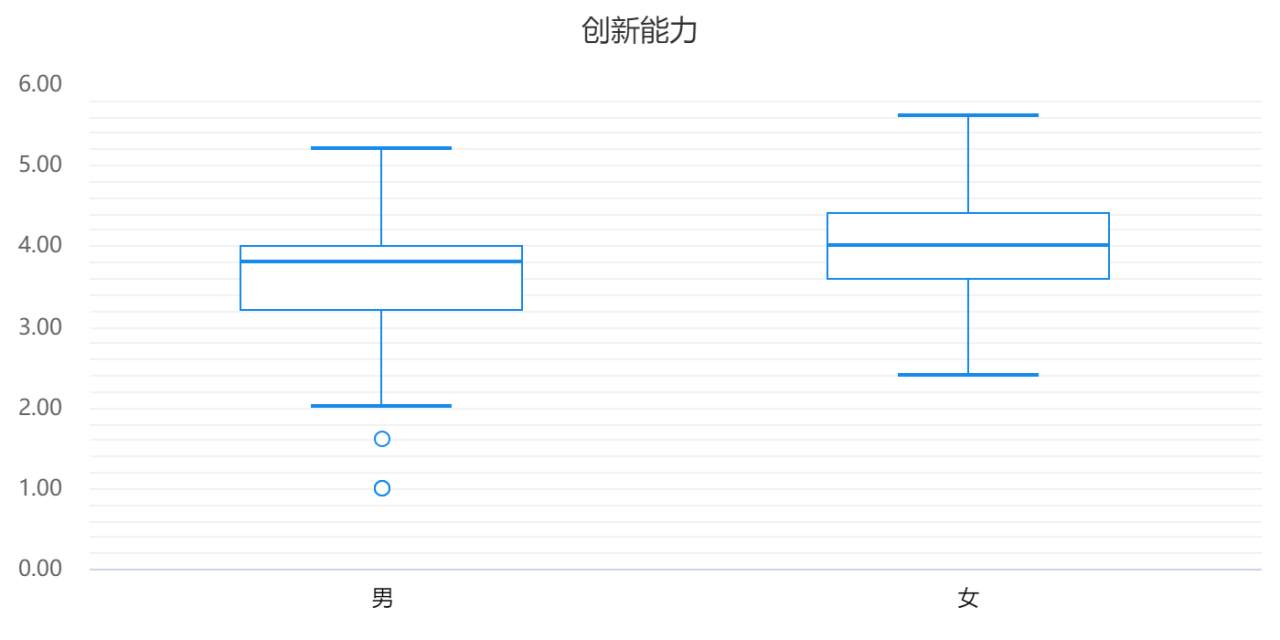
非参数检验分析结果
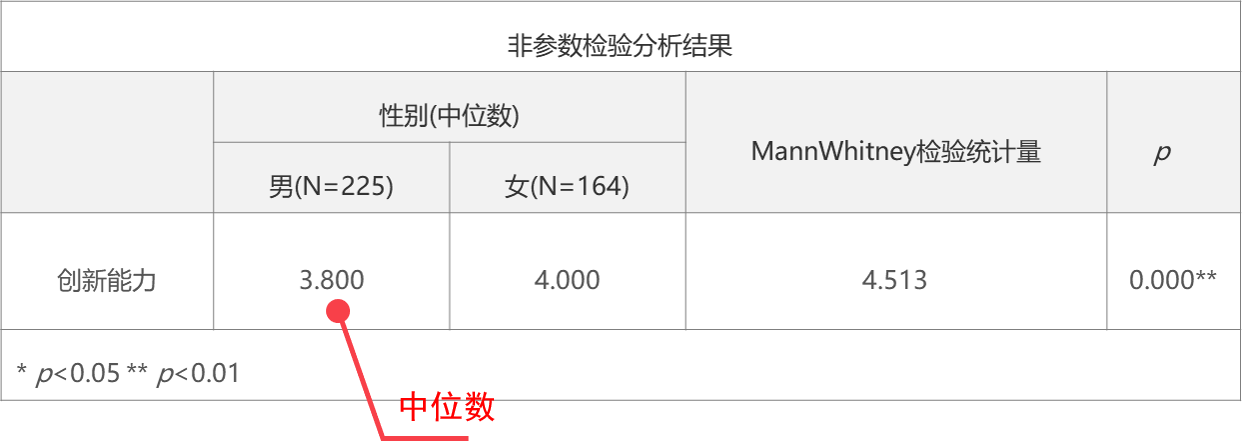
非参数检验结果中使用的是中位数描述差异。
④ 图形展示:
除了使用以上指标进行分析,还可以通过图形直观展示数据情况。参数检验常用图形有:折线图、条形图等,非参数检验可以使用箱线图查看。
3. 非参数检验的类型
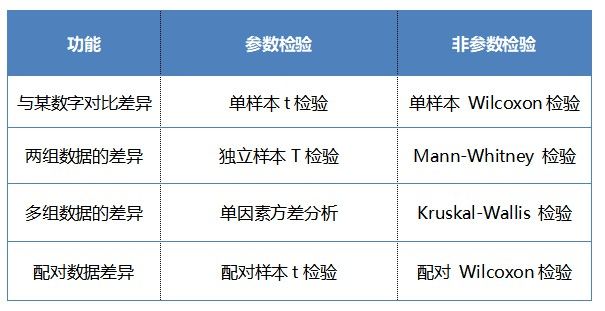
凡是在分析过程中不涉及总体分布参数的检验方法,都可以称为“非参数检验”。因而,与参数检验一样,非参数检验包括许多方法。以下是最常见的非参数检验及其对应的参数检验对应方法:
单样本Wilcoxon检验
单样本Wilcoxon检验是单样本t检验的代替方法。该检验用于检验数据是否与某数字有明显的区别,如对比调查对象整体态度与满意程度之间的差异。
Mann-Whitney检验
Mann-Whitney检验是独立样本t检验的非参数版本。该检验主要处理包含等级数据的两个独立样本,SPSSAU中称为非参数检验。
Kruskal-Wallis检验
Kruskal-Wallis检验是单因素方差分析的非参数替代方法。Kruskal-Wallis检验用于比较两个以上独立组的等级数据。
在SPSSAU中,与Mann-Whitney检验统称为“非参数检验”,分析时SPSSAU会根据自变量组别数自动选择使用Kruskal-Wallis检验或Mann-Whitney检验。

配对Wilcoxon检验
Wilcoxon符号秩检验是配对样本t检验的非参数对应方法。该检验将两个相关样本与等级数据进行比较。
4. SPSSAU操作
和参数检验一样,进行非参数检验时应当遵循以下的步骤:
案例:分析不同性别学生,学习成绩是否存在差异?
正态性检验
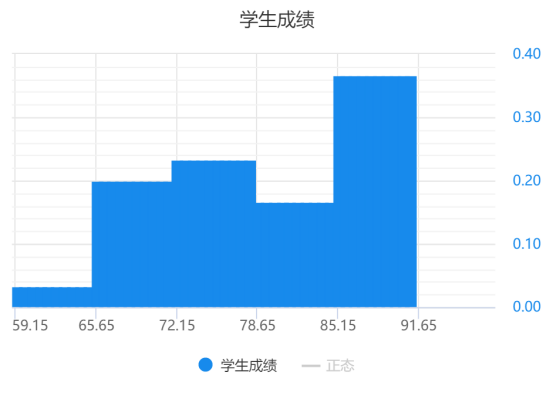
根据正态图显示,数据不服从正态分布,因而考虑使用非参数检验进行分析。
操作步骤
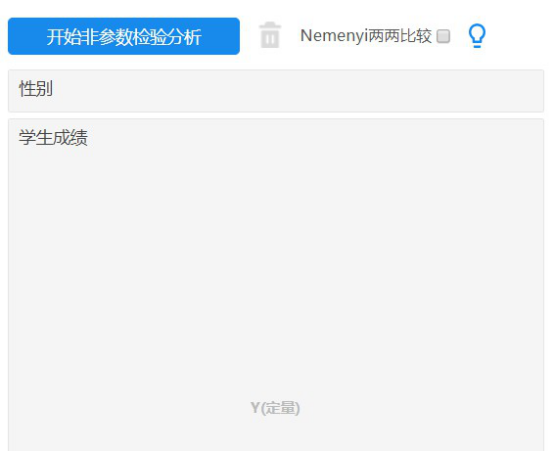
- 左侧方法栏点击【通用方法】→【非参数检验】;
- 将用于分组的自变量X放入【X(定类)】框;
- 因变量放入【Y(定量)】框;
- 点击开始非参数检验分析。
结果分析
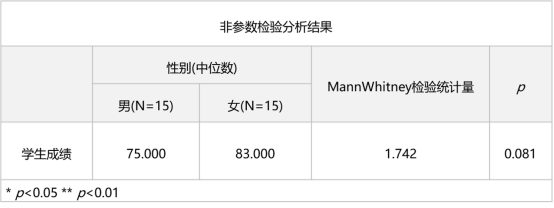
非参数检验分析步骤与参数检验步骤基本一致,建议参考SPSSAU输出结果中的“分析建议”及“智能分析”即可。

5. 两两比较
对应的方法是方差分析的事后检验,如果数据存在方差不齐或不服从正态性的情况,考虑使用非参数检验。
当结果呈现出显著差异时,如果想进一步对比两两组别,可以在分析前勾选“Nemenyi两两比较”。

6. 总结
以上就是非参数检验的流程梳理,事实上在大部分研究中,如果可以使用参数检验,即使不满足正态分布,也优先选择参数检验,尤其是在样本量较大的情况下。


