混杂因子亦叫混杂因素或外来因素(Confounder),是指与研究因素(暴露因子)和研究疾病(结局因子)均有关、若在比较的人群组中分布不匀,可以歪曲(掩盖或夸大)研究因素与疾病之间真正联系的因素。
①与结局因子(Y)相关;
②与暴露因子(E)相关;
③与暴露因子和结局因子的因果关系无关。
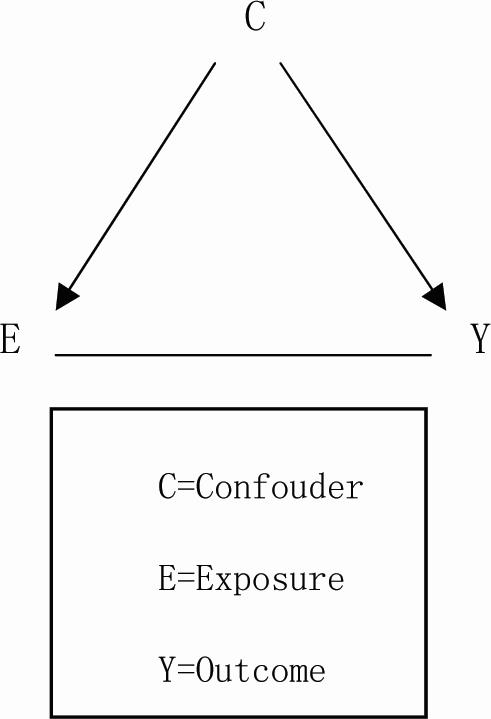
这是混杂因素成立的基本条件。具备这几个条件的因素,如果在比较的人群组中分布不均,即可导致混杂产生。如在关于吸烟与2型糖尿病关系的病例对照研究中,年龄、精神压力即具备这样的条件,如果病例组与对照组年龄分布不均衡,即可导致对吸烟与2型糖尿病关系的错误估计。
混杂因子的分类
大多数研究暴露因子与结局相关性的流行病学调查中,混杂因子可以大致分为三类:
(1) 必须校正的混杂因子
在暴露组与非暴露组中明显分布不均,会明确影响结论的混杂因子。
如:出生顺序(E)与唐氏综合征(Y)是否相关?
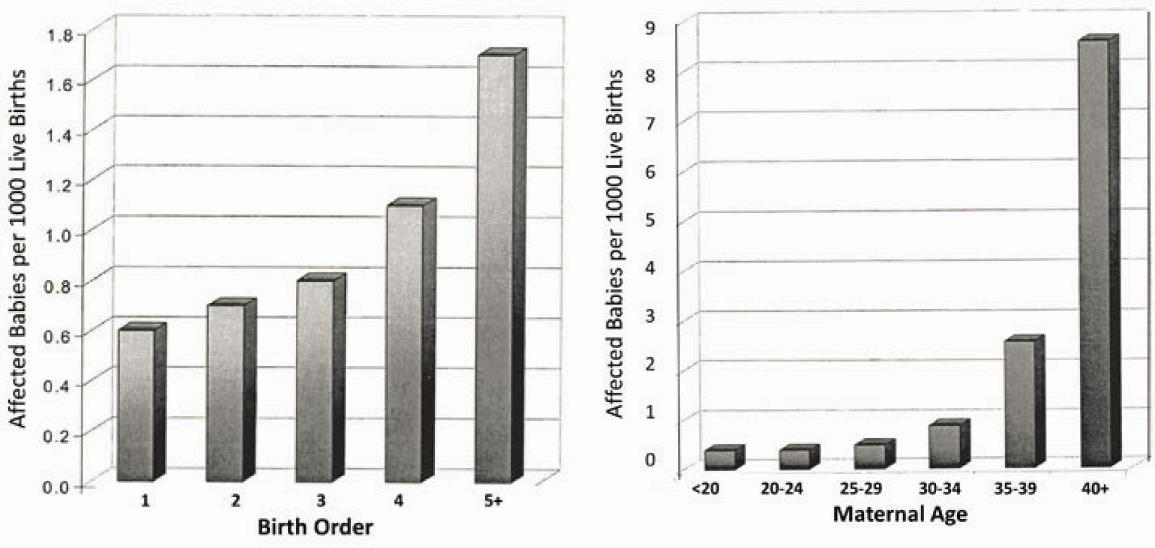
母亲的年龄就是一个显著的混杂因子,使得出生顺序与唐氏综合征的风险不再相关。
(2) 不可校正的混杂因子
那些与结局直接相关,但又与研究假说不相关的因子。
如:结局本身是由混杂因子X计算得来的
eGFR(肾小球滤过率)——血肌酐;
Framingham score——胆固醇、年龄、性别;
HOMA—IR(胰岛素抵抗因子)——空腹胰岛素、血糖
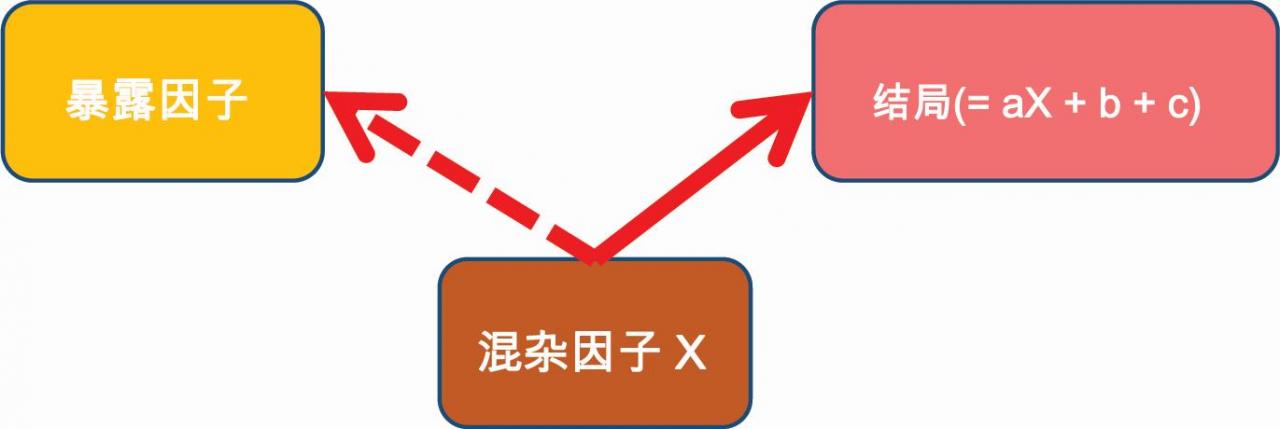
那些位于暴露因子与结局因果关系“中间”的因子
如:研究肥胖与糖尿病相关性时,应注意避免校正胰岛素抵抗,因为既往研究基本已经证实了肥胖导致胰岛素抵抗,从而导致2型糖尿病这一进程。
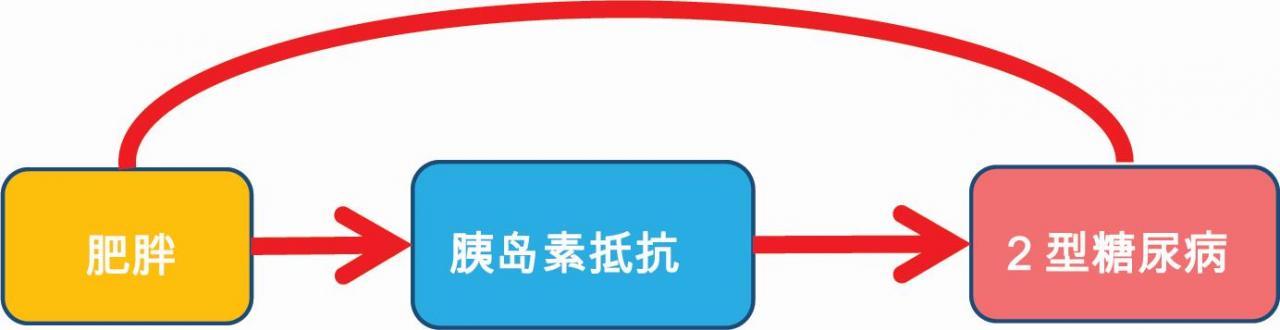
(3) 可选择校正的混杂因子
如:研究吸烟与2型糖尿病风险关系取决于研究假说和研究的关注点。

流行病学研究得出的结论往往都是相关性(association/correlation),但我们真正想探究的是真实的暴露因子和结局是否存在因果关系。而混杂因子会影响我们正确观察暴露因子与结局的关系,如果不能正确校正混杂因子的作用,研究结果会产生相当大的偏倚。那我们应该如何正确校正混杂因子呢?
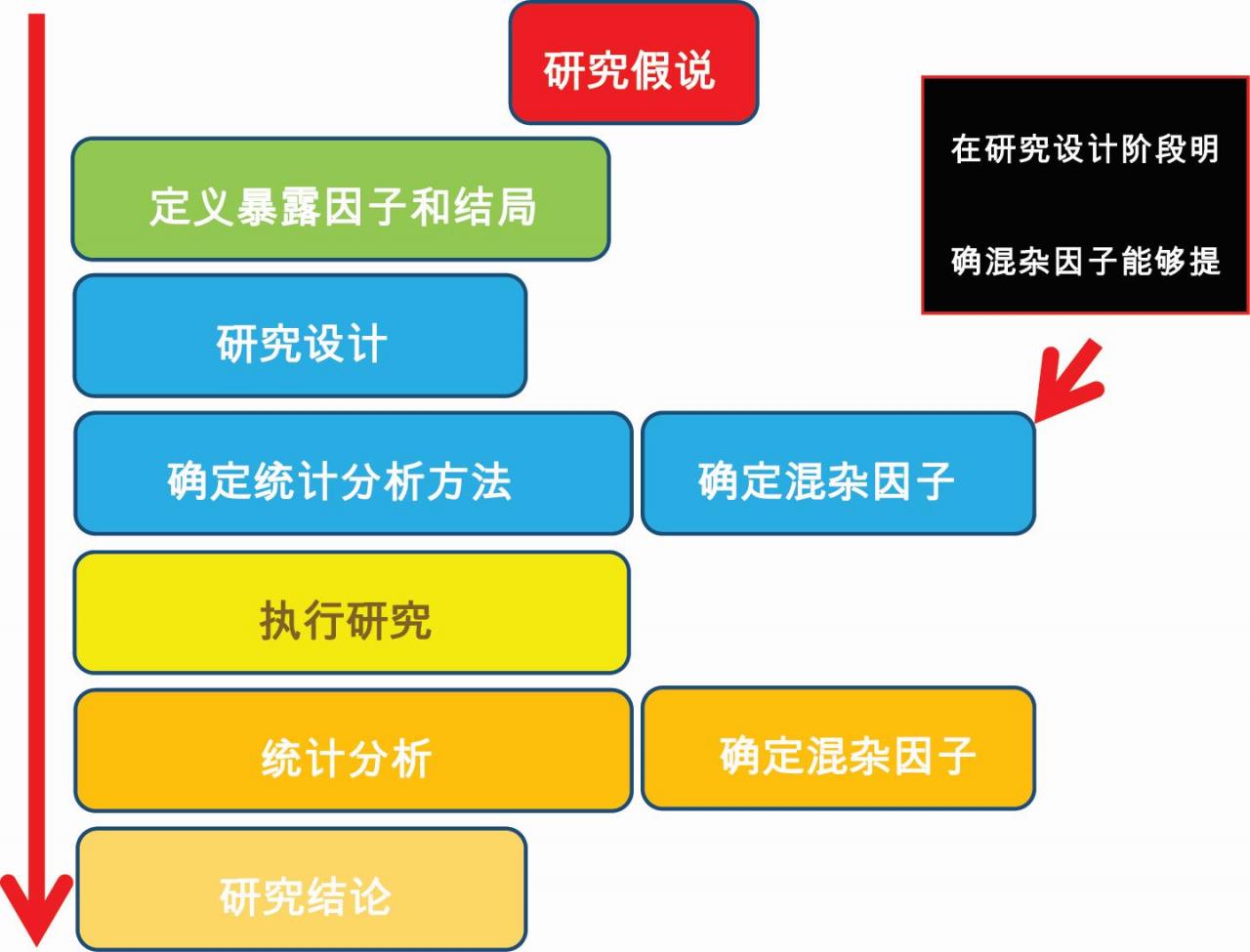
当发现回归分析中增加混杂因子X后,暴露因子与结局之间的关系不再显著。
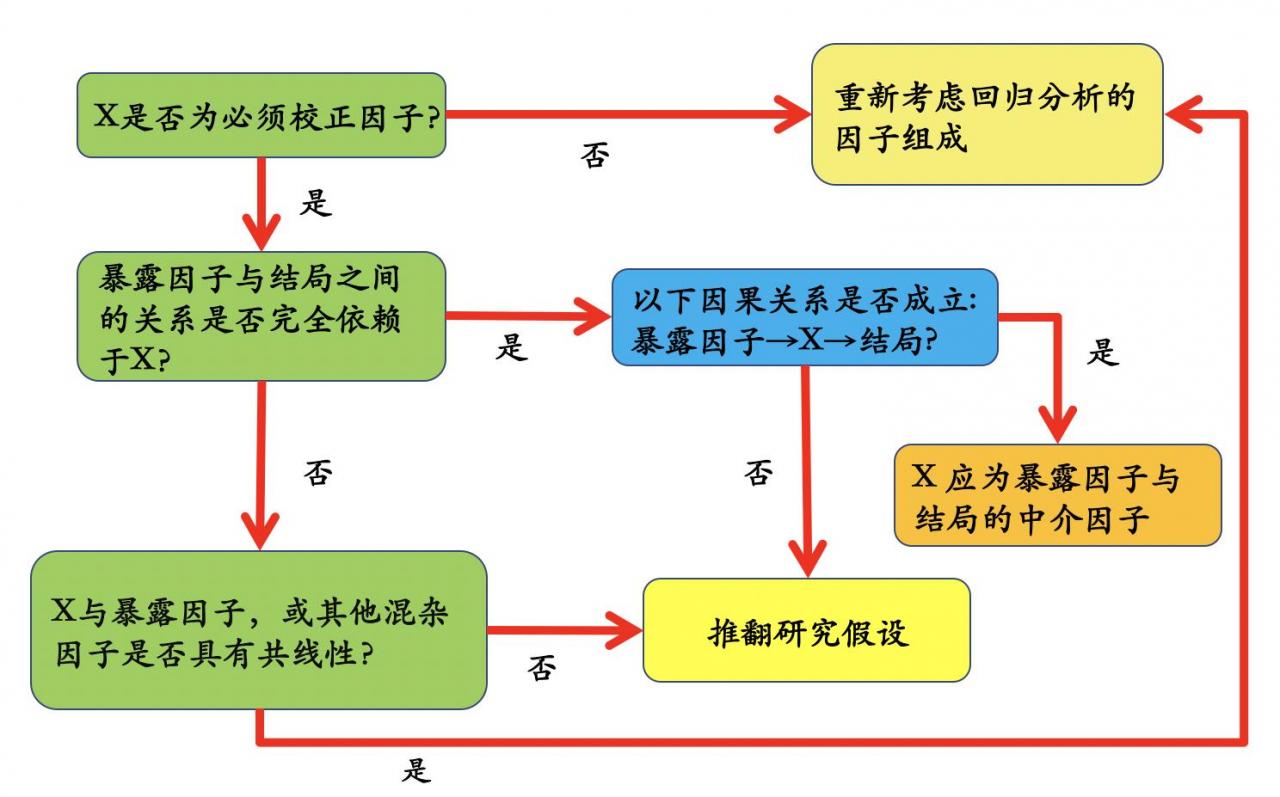
那是否应该针对X进行分层分析呢?
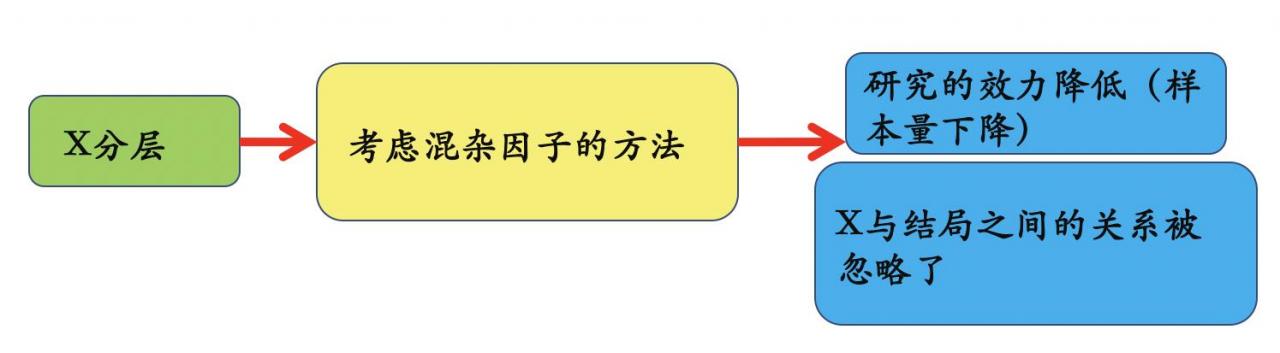
如:在吸烟和2型糖尿病相关性的研究中,性别是一个必须校正的混杂因子。若将人群分层后分别在男性、女性中观察吸烟和2型糖尿病的关系,那么无须再校正性别。但是,性别与2型糖尿病的关系在这个结果中就被忽略了。
通过以上学习,相信大家对于统计分析中混杂因子的相关内容有了一定了解,在今后的科研中需多加注意。本次课程小结:
混杂因子与暴露因子、结局二者皆相关,但是不应该位于暴露因子与结局的因果关系中间;
研究设计阶段就应该确定混杂因子;
统计分析阶段考虑混杂因子影响的方法有分层分析和回归分析中的校正;
一部分混杂因子可分为“必须被校正”和“不可被校正”两类,其余的混杂因子是否需要校正,取决于研究人员对于疾病的理解,而不是数字计算的P值。


