1. 因果性与相关性
1.1 什么是因果

什么是因果呢?“因”其实就是引起某种现象发生的原因,而“果”就是某种现象发生后产生的结果。因果问题在我们日常生活中十分常见。
首先在医疗方面。比如在这次新冠疫情中,各个国家都在争先恐后地研发疫苗,但在疫苗上市之前还需要做很多次单盲实验、双盲实验,其背后就是基于随机对照实验的一些因果推理和因果效应评估,确定药物于病人康复之间的因果效应。
其次在社会科学方面。比如在国家出台新的政策前,就要利用因果推理手段来估计这个政策会给民众、经济效应和社会效应带来多大影响。
最后在市场营销方面。比如在推广告之前,就需要使用随机对照试验或者A/B测试,选择广告推送的策略以实现效益最大化。
1.2 因果性与相关性的区别
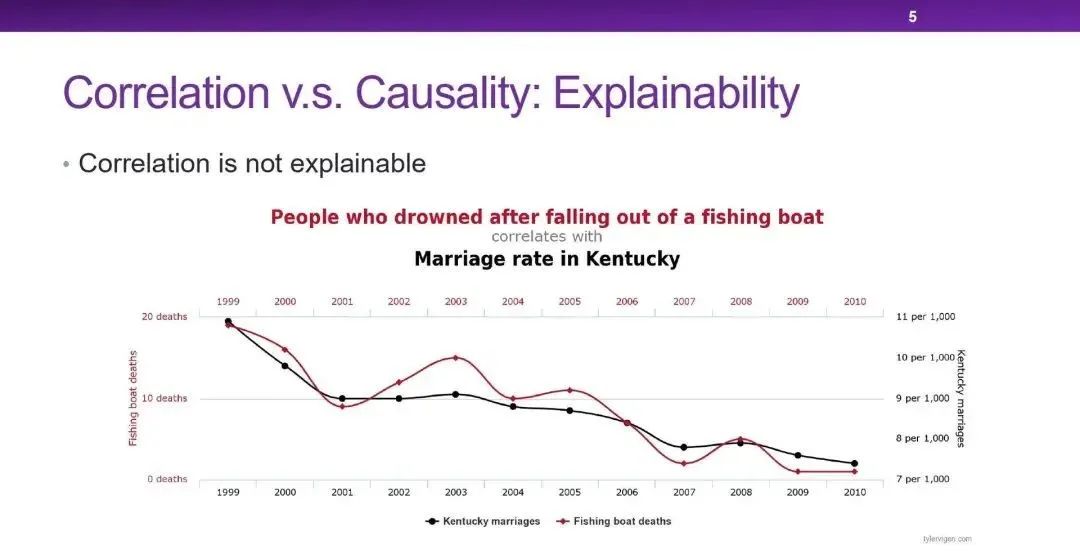
相关性比因果性更缺乏可解释性(Explainability)。这张图中,黑线是肯塔基州的结婚率,而红线是渔船事故死亡人数,两者具有很高的相关性,但两者之间却没有任何因果关系。我们在使用数据的时候就需要知道,这里的相关性是不可靠的、不可解释的。
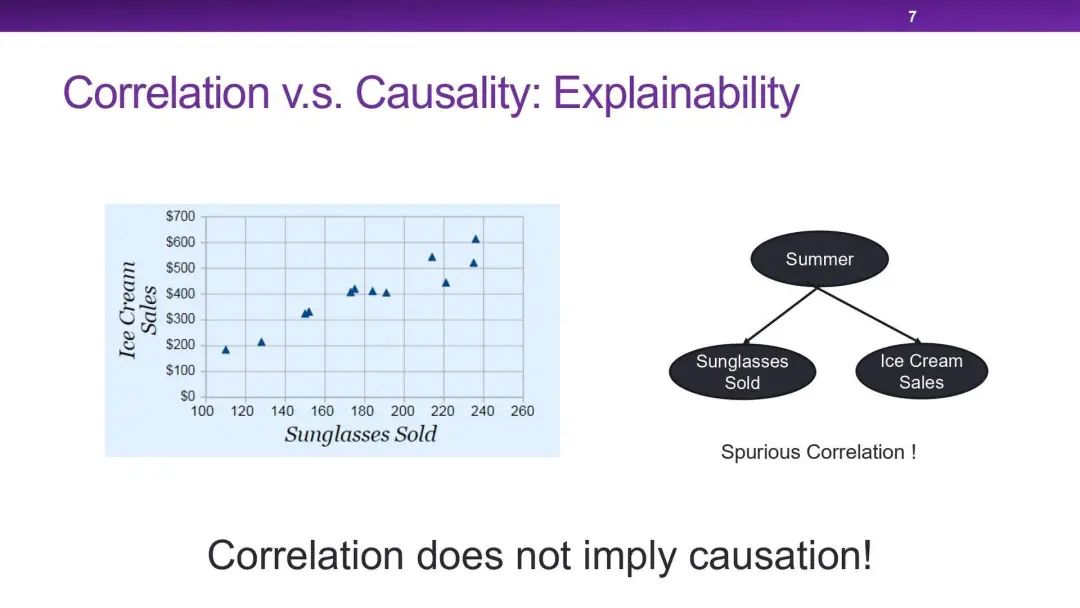
另外一个例子是太阳镜与冰淇淋的销售量之间的关系,两者之间呈现着明显的正相关性。但如果我们直接关闭太阳镜商店,进行干预,会影响冰淇淋的销量吗?并不会。因为两者之间的虚假相关性是由天气引发的,在太阳炎热时两者的消费量都会提升,强制干预其中一个的销量并不会直接影响另一个。

相关性比因果性更缺乏稳定性(Stability)。比如我们训练模型去识别图片中的狗,但数据集中90%的狗都是在草地上的,那么在这个数据集中草地与狗就十分相关。那么如果我们利用传统机器学习的方法,无论是逻辑斯蒂回归还是深度模型,大概率会把草地识别为重要的特征。但如果测试数据集中的狗是在沙滩上或者水中,模型就有很大概率会失败。
传统机器学习使基于关联驱动的,对于未知的测试数据集很难达到稳定预测。传统机器学习在关联挖掘中会发现一些非因果特征,比如草地背景与标签的关系,并利用这种强的虚假相关(Spurious Correlation)进行预测。如果我们能够发现特征与标签之间的因果关系,比如我们人类在识别狗的时候就会去关注够的鼻子、眼睛和耳朵这些因果特征,那么无论狗是在什么背景下,我们都可以正确识别。
第三个区别是可行动性(Actionability)。比如某个电商在推广某个商品时,需要从两个广告推荐算法中进行选择,看哪个算法能带来的收益更大。
如图所示,前期的试验发现,新算法B比旧算法 A 的总体成功率更高。但如果将用户按收入分为两层,却会发现算法A在低收入人群和高收入人群中的效果反而都优于 B 。两个算法的试验对象中,收入分布的差别很大,如果不进行控制,就会产生错误的结果。而除了收入之外,可能还需要考虑地域、年龄等多个变量,否则就会产生算法与成功率之间的虚假相关。
这些虚假相关是由混淆变量产生的混杂偏倚(Confounding Bias)。这种决策问题实际上是反事实问题,而不是预测问题。

第四个区别是公平性(Fairness)。Google曾开发了根据人像判断犯罪率的软件,输入为黑人时犯罪率就会比白人更高。而肤色与犯罪率之间不应该存在因果关系,这就出现了公平性的问题。实际上如图所示,真正起决定性作用的变量是“收入”,黑人的收入普遍偏低,而低收入人群的犯罪率较高,因此肤色和犯罪率之间出现了虚假相关。
而通过因果评估的框架,我们可以利用Do-演算(Do-Calculus)等工具,干预收入的多少,来计算肤色与犯罪率之间真正的因果效应大小。实际上,收入和犯罪率才是强因果相关的,而肤色和犯罪率之间因果效应可以弱到忽略不计。
1.3 相关性的三种来源

相关性有三种来源:因果、混淆和样本选择。
因果关联例子就是天下雨地面会湿,这种关系是能够被人类所理解的、是可解释的、稳定的(无论在任何国家或城市,天下雨地都会湿)。
混淆关联是由混淆偏差(Confounding Bias)造成的。比如图中X是T和Y的共同原因,但如果不对X进行观察,就会发现T和Y是具有相关性的,但T和Y之间是没有直接因果效应的,这就是产生了虚假相关。
样本选择偏差(Selection Bias)也会产生相关性,比如之前的例子中,如果数据集中的狗都出现在沙滩上,而没有狗的图片都是草地,那么训练处的模型就会发现草地与狗之间是负相关的,这也产生了虚假相关。
虚假相关与因果关联相比,缺乏可解释性,且容易随着环境变化。在工业界和学术界中,我们都希望能判断两个变量之间的相关究竟是因果关联还是虚假相关。如果是虚假相关的话,可能会给实际的系统带来风险。
所以说,恢复因果可以提高可解释性,帮助我们做出决策,并在未来的数据集中做出稳定而鲁棒的预测,防止算法产生的偏差。无论数据集中有什么样的偏差,我们都希望能挖掘出没有偏差的因果关系,来指导算法。
1.4 符号定义
这里给出关于因果的一个比较实际的定义:变量 T 的变量 Y 的原因,变量 Y 是变量 T 的结果,当且仅当在控制其他所有变量不变时,改变 T 会引发 Y 的变化。而因果效应(Causal Effect)就是改变变量 T 一个单位时,变量 Y 发生改变的大小。这里的两个重点是:一、只修改 T 的值,二、保持其他变量不变。

这里给出因果效应评估(Causal Effect Estimation)的数学形式。以评估药物的因果效应为例,干预变量(Treatment Variable)T 的值为1时代表吃了药,0代表没吃药,而这对应了两者不同的潜在结果。平均因果效应(Average Causal Effect, ATE)就是吃药的潜在结果与不吃药的潜在结果在所有病人上的差值平均值。个体因果效应(Individual Causal Effect, ICE)就是吃药的潜在结果与不吃药的潜在结果在某个病人上的差值。
这里还涉及反事实的问题:对于某个病人,我们只能观测到他吃药或不吃药其中一种情况的结果,想要探究未发生的另一种情况的结果,就需要假象存在一个平行世界,这个世界里病人做出了与之前不同的选择,除此之外都保持完全一致,对比两个世界的结果进行求解。
在实际应用中,随机化实验(Randomized Experiments)是因果效应评估的金标准。比如在疫苗研发中,就需要做双盲实验和单盲实验以评估因果效应。在足够大的实验人群中,通过完全随机的方法使其中一半人接种疫苗,这样就排除了其他变量的影响,求得平均因果效应。这种方法在政策评估、健康医疗和市场营销等多个领域都有重要应用,但这种方法的花销巨大,且可能涉及伦理道德问题。那么我们可否在巨量的历史观测数据中进行挖掘,评估出因果效应呢?

比如在一个数据集中,有吃药和未吃药的两群人。如果在数据收集时是使用单盲或双盲实验,那么就可以直接去计算平均因果效应。但如果没有保证分配药物的随机性,就可能会有体质、性别、年龄等混杂因子 X 使结果产生偏倚。因果推理的本质就是去控制吃药和不吃药的两群人之间其他特征的分布。
2. 因果效应评估的方法
现在我们考虑干预变量为二值的情况,要去平衡其他变量的分布,再做因果效应评估。在这里介绍三种方法:Matching、Propensity Score Based Methods 和 Directly Confounder Balancing。
首先给出在观测数据下做因果推理的三个假设:
一、Stable Unit Treatment Value (SUTV) 变量之间是独立的:我是否吃药的结果不受别人是否吃药的影响。
二、Unconfounderness 所有混淆变量都被观测到了。
三、Overlap 各种干预变量的取值概率都应该在0到1之间。
2.1 Matching
第一种方法叫 Mathching。在两个不同的处理群体之间,逐一寻找并匹配其他特征变量都相同的个体,如果找不到就舍弃此个体,这样就可以保证有匹配的那些样本中其他特征的分布在一定范围内是相似的,进而初步去评估因果效应。
Matching 的问题就是如何去评估两个个体的相似度,并需要设定可以接受的差异阈值,在舍弃样本数和相似度之间进行平衡。其次对于高维数据,很难找到相似样本:比如有10个二值变量,就需要至少1025个样本才能保证找到相同个体。
2.2 Propensity Score Based Methods

第二类方法是基于倾向指数/倾向得分(Propensity Score)的。倾向指数的定义就是在干预变量之外的其他特征变量为一定值的条件下,个体被处理的概率。Rubin 证明了在给定倾向指数的情况下,Unconfounderness 假设就可以满足。倾向指数其实概括了群体的特征变量,如果两个群体的倾向指数相同,那他们的干预变量就是与其他特征变量相独立的。
比如说,如果能保证两群人的他吃药的概率完全一样,那么可以说这两群人其他特征分布也是一样。

倾向指数在实际应用中是观测不到的,但可以使用有监督学习的方法进行估计。根据估计到的倾向指数,第一种方法就是去做 Matching,这样能解决在高维数据中难以找到相似样本的问题。

第二种是使用 Inverse of Propensity Weighting 方法,对于干预变量为1的样本使用倾向指数的倒数进行加权,而对于为0的样本使用(1-倾向指数)的倒数进行加权,两类样本的加权平均值之差就是平均因果效应的大小。这里有一个假设,就是估计出的倾向指数与真实的倾向指数是相等的。
因此这个方法有两个弱点,一是需要对倾向指数的估计足够精确;二是如果倾向指数过于趋近0或1,就会导致某些权重的值过高,使估计出的平均因果效应的方差过大。

第三种方法叫 Doubly Robust。这个方法需要根据已有数据,再学习一个预测的模型,反事实评估某个个体在干预变量变化后,结果变量的期望值。只要倾向指数的估计模型和反事实预测模型中有一个是对的,计算出的平均因果效应就是无偏的;但如果两个模型估计都是错误的,那产生的误差可能会非常大。

以上的这三种基于倾向指数的方法比较粗暴,把干预变量和结果变量之外的所有变量都当作混淆变量。而在高维数据中,我们需要精准地找出那些真正需要控制的混淆变量。我们提出了一种数据驱动的变量分解算法(D²VD),将干预变量和结果变量之外的其他变量分为了三类:
1. 混淆变量(Confounders):既会影响到干预变量,还会影响到结果变量
2. 调整变量(Adjustment Variables):与干预变量独立,但会影响到结果变量
3. 无关变量:不会直接影响到干预变量与结果变量
进行分类之后,就可以只用混淆变量集去估计倾向指数。而调整变量集会被视为对结果变量的噪声,进行消减。最后使用经过调整的结果,去估计平均因果效应。我们从理论上证明了,使用这种方法可以得到无偏的平均因果效应估计,而且估计结果的方差不会大于 Inverse of Propensity Weighting 方法。
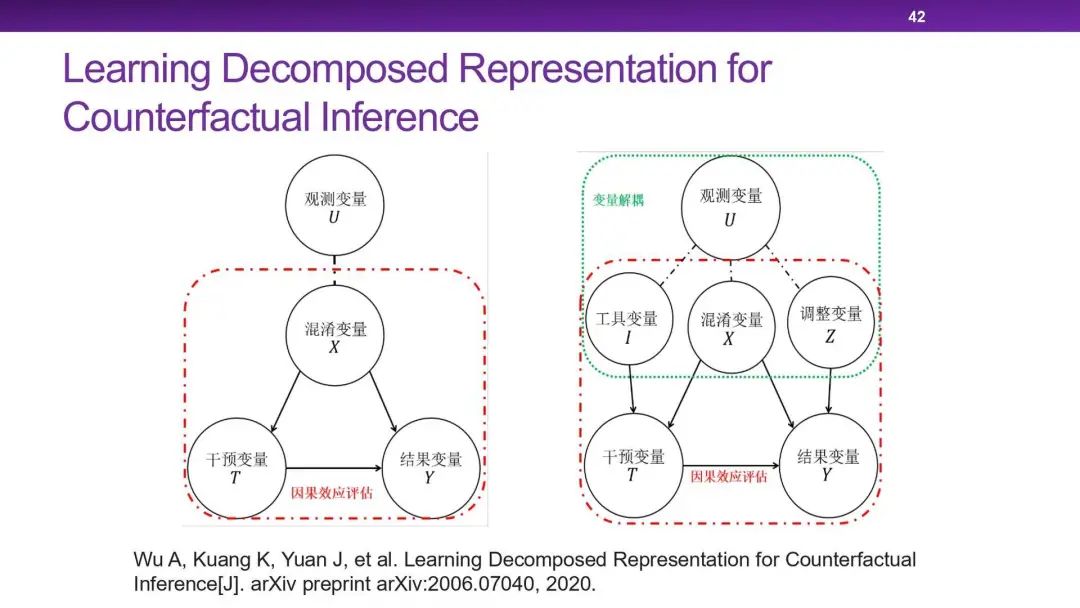
我的学生又拓展了我的工作,与表征学习相结合,提出了 Decomposed Representation。其中增加了一类变量:
4. 工具变量:与结果变量独立,但会影响到干预变量
通过实验发现,与传统方法相比,此方法可以很准确地把变量分离出来,提高平均因果效应的准确性。

2.3 Directly Confounder Balancing
总的来说,基于倾向指数的方法还是需要估计倾向指数的模型是准确的。既然倾向指数就是用于计算权重的,我们可不可以直接去估计权重呢?
第三类方法就是 Directly Confounder Balancing,直接对样本权重进行学习。这类方法的动机就是去控制在干预变量下其他特征变量的分布。而一个变量的所有阶的矩(moment)可以唯一确定它的分布,所以只需要去控制它所有阶的矩(比如一阶矩就是均值,二阶矩就是方差)就可了。在实验中我们发现,只考虑一阶矩就可以达到很好的效果,因此这里先不考虑二阶及以上的矩。通过这个手段就可以直接学习样本权重,进行平均因果效应估计了。

这个概念首先出现于 Entrophy Balancing 方法之中,通过学习样本权重,使特征变量的分布在一阶矩上一致,同时还约束了权重的熵(Entropy)。但这个方法的问题也是将所有变量都同等对待了,把过多变量考虑为混杂变量。

第二种方法叫 Approximate Residual Balancing。第一步也是通过计算样本权重使得一阶矩一致,第二步与 Doubly Robust 的思想一致,加入了回归模型,并在第三步结合了前两步的结果估计平均因果效应。只要样本权重的估计和反事实预测模型中有一个是对的,计算出的平均因果效应就是无偏的。但这里也是将所有变量都同等对待了。

我们提出的方法叫做混淆变量区分性平衡(Differentiated Confounder Balancing, DCB),考虑到的就是不同的特征变量对于平均因果效应的影响是不同的。我们在传统方法上加入了混淆变量权重(Confounder Weights)β:当β为0时,代表所对应的变量不是混淆变量,对因果效应不会带来影响;当β较大时,说明此变量对因果效应的影响较大。其中的β正好是从干预变量的增广到结果变量的回归系数。通过一系列实验发现,我们的方法在高维数据下对平均因果效应的估计偏差几乎为0,优于其他方法。
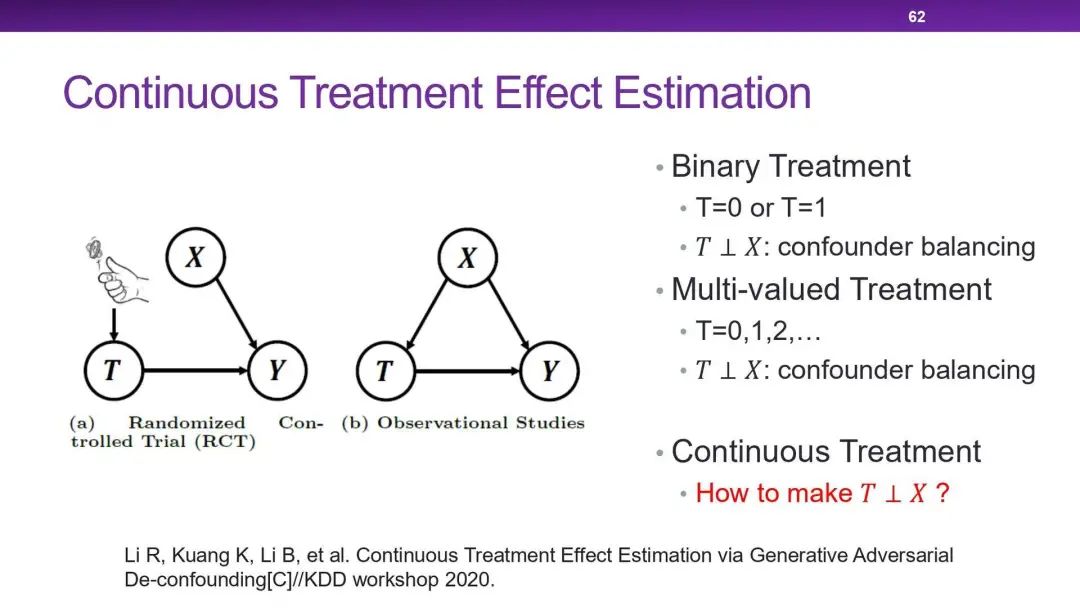
2.4 Generative Adversial De-confounding
上述的所有方法中,干预变量都是二值的,那如何去处理多值的或者连续的干预变量呢?我们今年的一个工作 Generative Adversial De-confounding 就尝试估计这类复杂情况下干预变量与结果变量之间的因果效应。这里的核心思想就是如何保证干预变量与其他特征变量的分布相独立。我们利用了 GAN 的思想,去凭空构造出另一个干预变量与其他特征变量相独立的分布。

我们使用了随机打乱(Random Shuffle)的方法,只打乱干预变量,这样就可以使干预变量与其他特征变量相独,并保留了两者的分布。我们再使用样本权重估计的方法,使原来数据集的加权分布结果与构造出的分布相一致。在实验中,可以发现我们的方法成功降低了干预变量与其他特征变量的相关性,并有效提高了因果效应评估的准确性。

参考文献:
[1] Kuang, K., Cui, P., Zou, H., Li, B., Tao, J., Wu, F., & Yang, S. (2020). Data-Driven Variable Decomposition for Treatment Effect Estimation. IEEE Transactions on Knowledge and Data Engineering.
[2] Wu, A., Kuang, K., Yuan, J., Li, B., Zhou, P., Tao, J., ... & Wu, F. (2020). Learning Decomposed Representation for Counterfactual Inference. arXiv preprint arXiv:2006.07040.
[3] Kuang, K., Li, L., Geng, Z., Xu, L., Zhang, K., Liao, B., ... & Jiang, Z. (2020). Causal Inference. Engineering, 6(3), 253-263.
[4] Kuang, K., Cui, P., Li, B., Jiang, M., Wang, Y., Wu, F., & Yang, S. (2019). Treatment Effect Estimation via Differentiated Confounder Balancing and Regression. ACM Transactions on Knowledge Discovery from Data (TKDD), 14(1), 1-25.
[5] Kuang, K., Cui, P., Li, B., Jiang, M., & Yang, S. (2017, August). Estimating treatment effect in the wild via differentiated confounder balancing. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 265-274).
[6] Kuang, K., Cui, P., Li, B., Jiang, M., Yang, S., & Wang, F. (2017, February). Treatment effect estimation with data-driven variable decomposition. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence.


