因为最近的课题需要用到单细胞多组学整合分析的方法,因此我学习了一下liger这个单细胞下游分析R包,觉得它的数学原理和整合方法都挺优美的,尽管软件包中有一大堆bug和不便之处。我将写一个liger单细胞多组学整合分析的系列博客,记录一下liger的数学原理的理解以及一些整合分析的代码,方便日后调用并避免一些软件包的bug和不便之处。
Liger是Evan Z. Macosko研究组2019年发表在Cell上的工作,Evan Z. Macosko也是单细胞RNA-seq领域内的大牛,Drop-seq就是他博后时的工作,他们实验室目前主要的研究方向是单细胞多组学测序与软件开发以及这些技术在神经细胞相关的研究中的应用。
数学原理
Liger使用非负矩阵分解(NMF)的方法对高维的转录组表达矩阵进行降维和聚类。矩阵分解本质上是坐标轴(空间中的一组基)的旋转,因此同一个矩阵可以进行无穷多种矩阵分解。
![]()
H矩阵是空间中固定的点,当旋转坐标轴W时,这些点在新的坐标轴上的投影就是X矩阵。由于空间中的基维度都是I,因此点坐标的信息不会丢失。当降低空间中的基的纬度时,我们便实现了数据的降维与压缩,并用约等号表示。
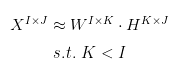
数据的降维一方面希望实现数据的压缩,另一方面也希望去除掉数据中的噪声,便于我们捕捉到真实的特征与信号。当然矩阵分解的方法是不唯一的,因为空间中基的旋转可以有无穷多种方式,基于一些约束条件,我们常用的矩阵分解的方法有以下三种。

PCA主成分分析根据方差最大的原则计算空间中使得数据方差最大的坐标轴,称为PC轴,因此其矩阵分解得到的值可正可负,在上面的图像处理的过程中相当于对不同的像素点进行可正可负的加权,由于负的像素点没有物理意义,因此这种矩阵分解的方法缺少一定的可解释性。VQ分解要求H矩阵中的每一列只有一个元素为1,其余元素均为0,因此W矩阵中的每一个元素都是一张特征脸。最后是非负矩阵分解,NMF要求W和H矩阵中的每一个元素都是正的,因此在图像处理的过程中,W矩阵中往往能捕捉到人脸的一些小的特征,如鼻子眼睛眉毛等,而图像合成的过程则是利用这些小的特征拼接成一张完整的人脸。更多对非负矩阵分解的理解与数学计算可以参考文献Learning the parts of objects by non-negative matrix factorization。
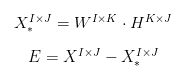
我们自然希望经过非负矩阵分解后降维压缩的数据与原始数据越像越好,因此定义一个Error项,不妨设E服从高斯分布,我们即可写出在给定参数下观察到E出现的概率,也就是E的极大似然函数,使极大似然函数出现概率最高的参数就是我们最终进行非负矩阵分解得到的W和H的各个元素(参数)。
![]()
![]()
![]()
目标函数可以使用梯度下降算法进行求解,具体的细节就不再展示。我们使用二范数的形式来简化目标函数。
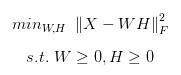
那么当我们有多个数据集并想将其整合起来的时候,我们要如何对上述的目标函数进行修正呢?16年第一篇使用非负矩阵分解的方法来处理单细胞转录组数据的文章A non-negative matrix factorization method for detecting modules in heterogeneous omics multi-modal data给出了integrate NMF的数学形式。
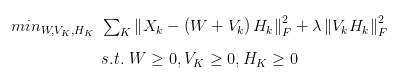
我们可以假定待整合的不同数据集之间必然存在着共有的一些特征,也必然存在着一些独特的特征。因此我们可以把原始W矩阵写成W矩阵与Vk矩阵的叠加,新的W矩阵则相当于不同数据集之间共有的特征,而Vk矩阵则是第k个数据集独特的特征。另外引入λ正则化项,λ的大小反映了数据集之间的相似性。当λ等于0时,VH的二范数对目标函数没有影响,因此在优化的过程中我们得到的W矩阵(也就是共有的特征)会趋向于0,而数据集独特的特征则会使得Error项尽可能的小,因此数据集之间的差异(也就是数据集独特的特征)就会尽可能的大。同理,当λ趋于正无穷大时,减小VH的二范数对优化目标函数的权重极大,在这种情况下,W矩阵,也就是数据集共有的特征,就会尽可能的大。
因此在进行非负矩阵分解的过程中,我们需要选择合适的参数K和λ,注意,这里的K指的是W矩阵的维度。在最理想的状态下,数据集中的每一个真实存在的cluster将占据W矩阵的一个纬度,此时数据之间分散得越开,H矩阵的KL散度就越大。因此参数K的选择可以基于H矩阵的KL散度进行优化,当KL散度刚刚饱和时的K应当是最优的K。同理,一般而言,我们希望在进行数据整合之后,不同数据集之间能够尽可能均匀的map在一起,这种均匀的程度可以用Alignment score进行衡量,随着λ的增大,我们假定的数据集之间的相似性越高,通常Alignment score就会越高。因此参数λ的选择可以基于聚类的Alignment score进行优化,当Alignment score刚刚饱和时的λ应当是最优的λ。但必须要指出的是,这种参数的优化仅仅基于通常无先验知识的情况,我们更建议以此为参考,根据我们对数据的理解和先验知识选择合适的参数。
Metagene
Metagene可以翻译成元基因,可以看成是一组基因的加权平均得到的一个pseudo gene,这个pseudo gene往往能表征某种细胞类型,并在这种细胞类型中特异性的高表达。定义这种metagene不仅能帮助我们定义不同的细胞类型,也能帮助我们找到数据集之间共有和差异的一些基因表达的特征,也就是metagene中high loading的基因。我们可以从liger的说明图中简单的进行理解。
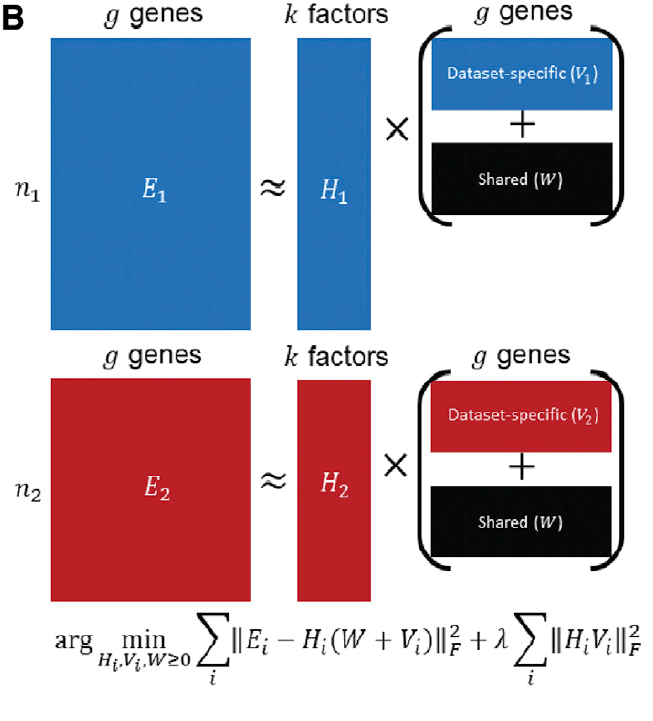
需要注意的是,我们通常习惯一行为一个基因一列为一个细胞的表达谱,但在liger的说明图中则做了个转置,因此根据矩阵的运算有以下公式。
![]()
因此在liger的说明图中,H矩阵做了转置并放在了W矩阵之前。将W或V矩阵中的每一行看成一个行向量,则每一个细胞的表达谱约等于W和V中所有的行向量的加权平均,权重则对应于H矩阵中该细胞所对应的行。因此liger的非负矩阵分解也可以理解为寻找到了低维空间中的metagene,单个细胞的表达谱则用这些metagene的loading value来进行表征(也就是H矩阵),利用这样一个新的表达谱再进行后续的进一步降维和聚类。
当然,我们可以寻找到一个metagene中对其贡献最大的基因,这样的gene可以是高表达该metagene的细胞类型的marker(如果这个metagene来自W矩阵),也可以是相同细胞类型的来自不同数据集之间的差异(如果这个metagene来自V矩阵)。
聚类
Liger的聚类算法也比较有意思,它并不基于单个细胞的坐标(label)进行聚类,而是用单个细胞周围k个邻居细胞的坐标(label)为该细胞赋予一个新的坐标,再根据曼哈顿距离或其他的范数距离进行聚类。Liger作者的观点是单个细胞被错误分配坐标(label)的概率要远大于其周围k个邻居细胞坐标都被系统性地错误分配的概率要高得多,因此使用周围k个邻居细胞的坐标来替代该细胞本身的坐标会使聚类的结果更加鲁棒。

应用
基于非负矩阵分解的方法,liger可以用于整合不同的单细胞RNA-seq数据集,甚至差异特别巨大的多组学单细胞数据集。后续的博客将会介绍:
参考文献
[1] Welch J D, Kozareva V, Ferreira A, et al. Single-cell multi-omic integration compares and contrasts features of brain cell identity[J]. Cell, 2019, 177(7): 1873-1887. e17.
[2] Yang Z, Michailidis G. A non-negative matrix factorization method for detecting modules in heterogeneous omics multi-modal data[J]. Bioinformatics, 2016, 32(1): 1-8.
[3] Lee D D, Seung H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788-791.


