置换检验（Permutation test）

来源：Hua's Cabin评论3,835

置换检验

置换检验，是Fisher提出的一种基于大量计算（computationally intensive），利用样本数据的随机排列（置换检验的核心思想，故名Permutation test），进行统计推断的方法。因其对总体分布自由，特别适合用于总体分布未知的小样本数据，以及一些常规方法难以使用的假设检验情况。

原理

在零假设成立情况下，根据研究目的构造一个检验统计量（如均值，方差等），对样本进行随机抽样并根据排列组合进行随机分组，每次分组均可以计算得到一个检验统计量，由于排列组合次数较多，因此可以得到许多检验统计量，模拟检验统计量的分布，然后求出该分布中出现观察样本的均值（原始均值）及更极端样本的概率p，通过和显著性α比较，做出统计推断。

步骤

提出原假设，如A组（m个元素）和B组（n个元素）没有差异；
计算统计量，如两组的均值之差μ0=μA−mu_B$；
将所有样本随机排序并根据A和B组的数目随机分组，计算统计量μ；
重复步骤3，直到所有排列组合计算统计量完毕，统计量个数为mu1 μm个；
最后将步骤4得到的所有统计量按照从小到大排列后构成分布，观察步骤2计算得到的观察样本μ0落在该分布的位置（如95%的置信区间：一倍方差内），并计算小于该观察值的所有统计量的数目占所有统计量数目的比例p，若p落在置信区间内（双侧检验）则接收原假设，否则拒绝；
如果第3步骤是将所有可能性都计算了的话，则是精确检验；如果只取了计算了部分组合，则是近似结果，这时一般用蒙特卡罗模拟（Monte Carlo simulation）的方法进行置换检验；
置换检验和参数检验都计算了统计量，但是前者是跟置换观测数据后获得的经验分布进行比较，后者则是跟理论分布进行比较。

优点

不需要知道基础数据的分布；
能处理多种类型数据；
方法简单且相对容易解释;
适合不满足传统分析方法的条件的数据，如小样本数据等。

实例

permutation test 原理实现过程

a <- c(24,43,58,67,61,44,67,49,59,52,62,50,42,43,65,26,33,41,19,54,42,20,17,60,37,42,55,28)
group <- factor(c(rep("A",12), rep("B",16)))
data <- data.frame(group, a)
mu_sob <- mean(data[group=="A",2]) - mean(data[group=="B",2])


find.mean <- function(x){
mean(x[group=="A",2]) - mean(x[group=="B",2])
}

results <- data.frame(value=replicate(999, find.mean(data.frame(group,sample(data[,2])))))
p.value <- length(results[results > mu_sob]) / 1000

confidence_interval <- function(vector, interval) {
vec_sd <- sd(vector)
n <- length(vector)
vec_mean <- mean(vector)
error <- qt((interval 1)/2, df = n - 1) * vec_sd / sqrt(n)
result <- c("lower" = vec_mean - error, "upper" = vec_mean error)
return(result)
}
ci_95 <- confidence_interval(results$value, 0.95)


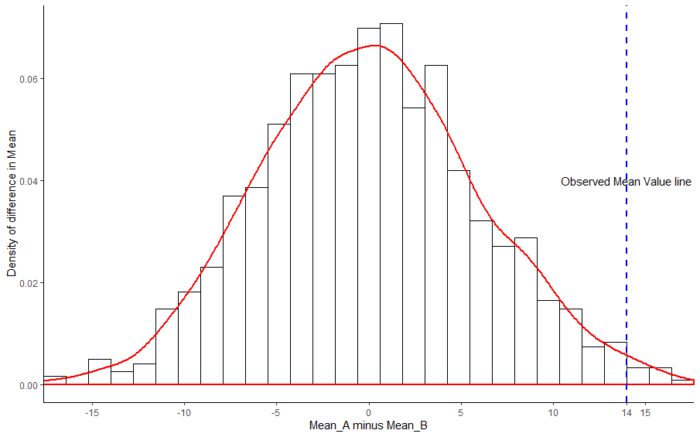
ggplot(results, aes(x=value))
geom_histogram(aes(y=..density..), colour="black", fill="white")
geom_density(alpha=.8, color="red", size=.8)
geom_vline(xintercept=mu_sob, linetype="dashed", color="blue", size=1)
scale_x_continuous(breaks = c(-15,-10,-5,0,5,10,14,15),
labels = c(-15,-10,-5,0,5,10,14,15),
expand = c(0, 0))
annotate("text", x=14, y=0.04, label="Observed Mean Value line")
labs(x="Mean_A minus Mean_B", y = "Density of difference in Mean")
theme_classic()

置换检验（Permutation test）

使用coin包实现上述分析过程

Input = ("
 Individual  Hand     Length
 A           Left     17.5
 B           Left     18.4
 C           Left     16.2
 D           Left     14.5
 E           Left     13.5
 F           Left     18.9
 G           Left     19.5
 H           Left     21.1
 I           Left     17.8
 J           Left     16.8
 K           Left     18.4
 L           Left     17.3
 M           Left     18.9
 N           Left     16.4
 O           Left     17.5
 P           Left     15.0
 A           Right    17.6
 B           Right    18.5
 C           Right    15.9
 D           Right    14.9
 E           Right    13.7
 F           Right    18.9
 G           Right    19.5
 H           Right    21.5
 I           Right    18.5
 J           Right    17.1
 K           Right    18.9
 L           Right    17.5
 M           Right    19.5
 N           Right    16.5
 O           Right    17.4
 P           Right    15.6
")

Data = read.table(textConnection(Input),header=TRUE)

library(coin)
# Permutation test of independence
independence_test(Length ~ Hand, data = Data)

#Asymptotic General Independence Test
#Z = -0.34768, p-value = 0.7281


# Permutation test of symmetry 适用repeated data
symmetry_test(Length ~ Hand | Individual, data = Data)

#Asymptotic General Symmetry Test
#Z = -2.6348, p-value = 0.008418

引用

Permutation