Permutation test,也称置换检验,随机化检验或重随机化检验,是大牛Fisher首次提出的。由于Permutation test检验计算量大而限制了其应用和推广,以致不为人熟知。现在由于计算机技术飞速发展,Permutation test又重新进入我们的视野。Permutation test有独特的优势,其对原始数据分布没有要求,特别适用于不满足传统分析方法的条件,比如小样本数据。另外,对于一些复杂设计难以用传统方法解决时,不妨试试Permutation test。
研究表明,当样本含量较大时, Permutation test得到的结果与经典的参数检验(t 检验、F 检验)近似。当样本含量较小时,Permutation test要优于参数检验,并且其检验效能也高于秩和检验。实际上,Permutation test的应用远不止于此,感兴趣的亲们可以进一步深入学习。今天,我们只是对Permutation test做一个简单的介绍。
Permutation test的基本思想是:在H0假设成立的前提下,根据研究目的构造一个检验统计量,并利用样本数据,按排列组合的原理,导出检验统计量的理论分布,在实际中往往因为排列组合数太多,而模拟其近似分布,然后求出在该分布中出现观察样本及更极端样本的概率p,通过和0.05比较,做出统计推断。
如果p>0.05,表明H0假设成立时,观察样本的出现是很平常的,也就是说不拒绝H0假设;如果p<0.05,表明H0假设成立时,观察样本的出现是小概率事件,基于小概率在一次样本中基本不发生的原理,可以认为H0假设不成立,也就是不接受H0假设。
说了这么多,Permutation test具体怎么操作呢?以两样本数值变量比较为例,比如,有两组数据,第一组:40,45,55,57,58;第二组:55,57,62,64,65。
第一步:建立H0假设:两样本来自同一总体。
第二步:构造统计量,比如采用两组均数之差,第一组均数为51,第二组均数为60.6,两组均数差的绝对值为9.6(因默认双侧检验,所以这里用的绝对值)。
第三步:在H0假设的前提下,即两样本来自同一总体,对样本重新分组,也就是将上述10个数值随机分成两组,每组5个数值,每组重新分组时,均计算均数差。10个数随机等分为两组,共有252种情况,也就是说我们会得到252个均数差。
第四步:求出p=252个均数差中≥9.6的个数/252。
第五步:作出推断,如果p>0.05,说明在两样本来自同一总体的假设下,当前样本的出现是很平常的,不能拒绝H0假设,认为两样本的差异无统计学意义;如果p<0.05,则认为两样本的差异有统计学意义。
每组5个数值,一共两组,已经是很简单的情况了,竟也要252种情况,若是没有强大的计算机功能,还真的很难,也就是为什么之前Permutation test未能广泛推广的原因。幸好我们这个时候,完全不担心这些问题。
那么问题来了?到这里,大家还是感觉第一次接触Permutation test,怎么会是小编说的【一直在用呢】。因为,小编发现SPSS其实提供了Permutation test的结果。大家知道在卡方检验的【精确】选项有三种选择:渐进法、蒙特卡洛、精确,英文为asymptotic、approxiamate、exact。这其实就是Permutation test,渐进法、蒙特卡洛是通过模拟得到统计量的分布,而exact是用所有排列组合构建统计量的分布。另外,在非参数检验的结果中,大家常会看到渐进显著性和精确显著性,这其实就是Permutation test。是不是可以说非参数检验其实已经被偷偷替换成Permutation test了呢?看到这里,您是不是有一种恍然大悟的感觉,的确原来一直在用啊。
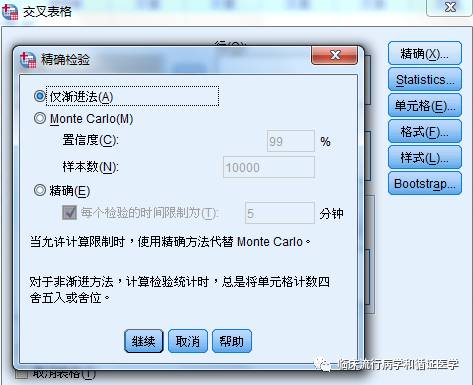
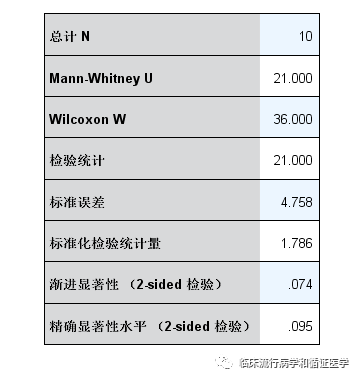
SPSS给出了非参数检验和卡方检验Permutation test的结果,但SPSS并未提供相关、回归相应的Permutation tes的结果,这就需要我们借助Stata、SAS、R等软件了。这解决了小编一直以来的困惑,比如x、y变量分别有10个数据,如果想探讨二者之间的关系,感觉数据太少,相关和回归是否合适呢?现在,直接用Permutation test就可以了呀。当然,Permutation tes的应用还是很广泛的,比如ROC曲线的比较、生存资料分层分析、基因差异表达分析等。


