p值是现在常用的统计学指标。当我们检验一个统计假设H0时,p值是当H0为真时样本结果或者更极端结果出现的概率。p值越小,也就越应该拒绝原假设,也就是结果越显著。在现在的生物医学研究中,一般的显著性标准是p值<0.05。但这个标准最近几年引发了非常多的争议,比如虽然很多癌症研究都声称自己达到了0.05的显著性,但很多结果的可重复性并不高。p值的误用也比较多见。nature在2014年,nature和science在今年都专门讨论了如何理解p值,以及如何界定研究的显著性[1-3]。
在今年7月,统计学家们发表了一篇新文章,希望能够提高研究中显著性的标准,从而提高结果的可重复性[4]。他们推荐用一个更严格的p值,0.005取代目前常用的0.05. 这篇文章于7月22日发表于PsyArXiv,第一作者为来自加州大学洛杉矶分校的DanielBenjamin,他认为类似的做法在其他领域已经取得了成功,比如在测序数据分析上,人们已经采用更为严格的p值。这场变革的支持者认为,这种做法可以显著减少研究结果中的假阳性-即宣称某个结果为真,但事实上并没有这个效果。但是其他科学家拒绝接受p值的绝对标准。他们担心这只会增加临床研究的花费。卢森堡健康研究院的StephenSenn评论说,他认为这个结果并不怎么样,我觉得这些人没搞清楚他们到底在干什么。
基本概念
为了理解这篇文章,我们需要明确一些基本概念。
统计功效(power):简单讲就是通过实验等手段发现一个事实的概率。比如某种药物可以杀死癌细胞,如果统计功效是0.9,就表明通过实验有0.9的概率可以发现它杀死癌细胞。那么在这种情况下,就有0.1的概率,即使这种药物是有效的,但癌细胞在实验中并没有被杀死。这里的0.1就是二类错误的概率,也就是假阴性错误概率[5]。统计功效一般用1-beta表示,其中beta是二类错误的概率(type II error)。统计功效和实验的可靠性有关,理想情况下应该趋近于1,但在现实中对于较为复杂的实验,往往不会有那么高。
显著性水平(alpha,type I error),也就是我们这里讨论的p值。它也是一类错误的概率,即假阳性概率[6]。我们目前的标准是0.05。对于基本的统计检验,我们都可以通过查表来判断其是否达到相应的显著性水平。
贝叶斯因子(Bayesfactor)和先验风险(prior odds)。贝叶斯因子是H1假设下得到观测xobs数据的概率除以零假设下得到观测数据的概率。alpha(显著性水平)越小,贝叶斯因子越大。贝叶斯因子和先验风险通过贝叶斯公式联系在一起。通过观测数据我们认为H1假设和H0假设的比值满足
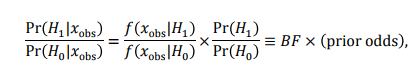
贝叶斯因子可以看做从数据得到的关于H1假设和H0假设的信息。而先验风险则跟研究者的具体问题,科学共识有关。我们也可以把prior odds表示为(1-phi)/phi,其中phi为Pr(H0),即零假设成立的先验概率。
文章结果
让我们回到这篇文章,这篇文章的主要结果可以用一张图来概括(Fig 2)。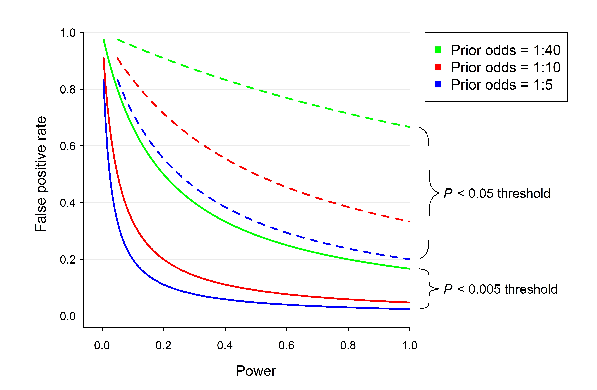
这张图基于以下的公式
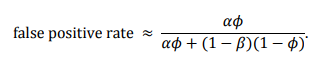
其中我们发现phi越大,假阳性结果的概率越大。而显著性越强,alpha越小,假阳性越低。类似统计的功效越大,beta越小,假阳性越低。在这张图中我们可以发现alpha也就是显著性水平的影响。我们发现当alpha=0.05时,如果先验风险是1:10,那么结果假阳性的概率至少大于33%。当我们采取的p value为0.005时,假阳性结果的概率就在很多时候小于10%。
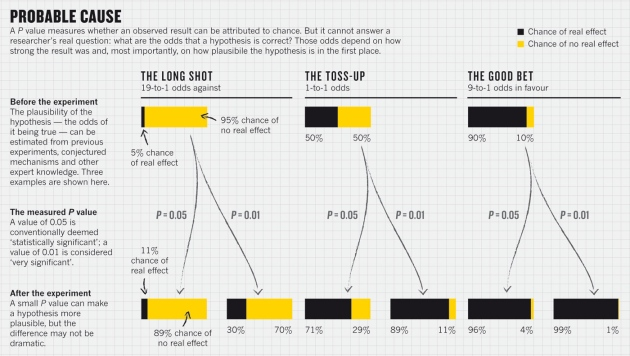
我们也可以用nature杂志2014年的一张图来说明这一问题[3]。这张图黑色显示的是有实际作用的可能(H1假设成立),黄色是H0假设成立的概率。第一行是我们之前提到的先验风险,左侧是prior odds=1:19,中间是1:1,右边是比较好的情况9:1,也就是H1概率比较大。第二行是在显著性水平为0.01或者0.05的情况下H0和H1的后验概率。可以发现在右边,当H1概率比较大时,这两个p值结果相差不大。而在左边,当H1概率为5%左右时,p=0.01情况下H1的后验概率比p=0.05情况下大了两倍左右。也就是在这种情况下,p值较小带来的概率改善更大(2倍vs6倍)。对于H1和H0概率相差不大的情况,我们发现p=0.01和p=0.05带来的改变差别就没有那么明显(1.4倍vs1.8倍)。
小结
关于这篇今年发表的文章,大家也是评价不一,可以参考[1]一文中的报道。即使是一些支持者,也对显著性是否应该有绝对值,以及绝对值应该定成多少有不同意见。在反对者中,有看法认为这种倡议可能会加剧p值作弊的现象(p-value hacking),就是只发表阳性结果而把其他结果藏起来。另一些人担心提高p value需要更多的样本,也就要更多的研究经费。比如在一般情况下(正态分布),把p值从0.05提高到0.005可能需要增加70%的样本。
不过这篇文章还是可以帮助我们思考p值的含义。从本质上讲,p值只是结果在现有实验条件下是否可能是随机产生的度量,它对应的因果链是p值越小,结果越不可能随机产生,贝叶斯因子也就越大。但这不代表Pr(H1|xobs)/Pr(H0|xobs)就越大。因为根据上述的公式,它还依赖于H1和H0概率的比值,也就是先验风险。举一个不那么恰当的例子。假设H0的概率为1,H1的概率为0,也就是一个命题不可能为真。但有全世界有30个实验室做同样的实验,很大概率有一个实验室得到了显著性为0.05的结果来说明命题为真(贝叶斯因子仍然很大),并写成一篇文章[8]。但显然这样的结果没有任何意义。
很多时候在生物及医学领域的研究,可能并不是为了证明某个命题为“真”。而是通过研究构筑的逻辑链条(或者对定量数据的总结推断),来提高某个命题为真的后验概率。一个决定性的研究可以让我们相信某个命题为真的概率趋近于1.而对于存在多个解释的问题,我更愿意相信这些解释成立与否也是概率事件。那么研究的进步也就是降低这些概率事件对应的信息熵,直到我们有一个确定的理论。从这个角度讲,p值低是有好处的。从现实的角度我们也可以做一个估算,有人计算说有53%的临床前研究是不可重复的(并且大约浪费了280亿美元的经费)[9]。假设我们认为这个数字是合理的,然后取p=0.05,可以估算对应的prior odds约为1:10.这个数字表明大家习惯从较弱的数据出发。我们也应该意识到这一因素对于设计实验和诠释结果的影响。另外在进行试验设计和结果诠释的时候,研究者的科学判断(也是对先验风险的估计)也是十分重要的。当H1的先验概率较弱时,也就是我们的结果显得非常惊人的时候,往往也需要更严格的p值检验。
reference:
[2]http://www.nature.com/news/statisticians-issue-warning-over-misuse-of-p-values-1.19503
[3]https://www.nature.com/news/scientific-method-statistical-errors-1.14700
[4]https://www.nature.com/articles/s41562-017-0189-z
[5]这里的假阴性应该这样理解。我们的零假设(H0)是药物对癌细胞没有作用,结果我们有0.1的概率得到结果就是癌细胞没有死亡,支持了零假设。这是阴性结果(没有拒绝0假设),同时也是错误结果。所以是假阴性错误。
[6]同[5],仍然需要零假设为药物对癌细胞没有作用。
[7] 即虽然显著性水平达到要求,拒绝了零假设,但其实零假设成立.
[8] 而且从概率上讲,只要做的实验室足够多,这种结果也是可以“重复”的。


