如果我想看不同患者人群的术后复发率有没有差异,怎么办?这时候就需要欢迎我们的统计小助手——卡方检验闪亮登场啦!
卡方检验可是一位重量级选手,凡是涉及到计数资料分布的比较都需要他的帮忙。和t检验一样,卡方检验也会用在成组和配对设计资料分析中,本期我们一起聊聊独立样本四格表的χ2检验。
一、问题与数据
用药物A治疗急性心肌梗死患者198例,24小时内死亡11例,病死率为5.56%,另42例治疗时采用药物B,24小时内死亡6例,病死率为14.29%,提问:两组病死率有无差别?
表1. 两种药物急性心肌梗塞患者治疗后24小时内死亡情况

二、对数据结构的分析
“生存”,还是“死亡”,这是个问题,但更是一个典型的二分类结局指标,我们关注的重点是两种药物治疗后“生存”和“死亡”的分布(或者说病死率)有无差别,由此组成的2*2列联表就是χ2检验中经典的“四格表”(如表1)。
下面一起看看SPSS怎样搞定χ2检验。
三、SPSS分析方法
1. 数据录入
(1) 变量视图

(2) 数据视图
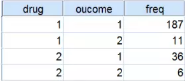
2. 加权个案:选择Data→weight cases→勾选Weight cases by,将频数放入Frequency Variable→OK。因为本例中数据库每一行代表多个观测对象,所以需要对其进行加权处理。
当然,如果数据是以单个观测对象的形式,即每一行代表1个观测对象,则无需加权(如下图)。
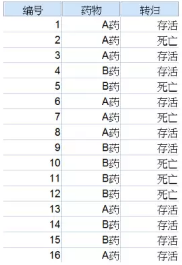
3. 选择Analyze→Descriptive Statistics→Crosstabs
4. 选项设置
(1) 主对话框设置:将分组变量Drug放入Row(s)框中→将指标变量Outcome放入Column(s)框中(实际上χ2检验是关注实际和理论频数是否一致,这里Row(s)框和Column(s)框内变量也可以颠倒放,并不影响最终结果)。
(2) Statistics设置:勾选Chi-square,确定使用成组计数资料的卡方检验→Continue
(3) Cells设置:Counts中勾选Observed和Expected,输出实际观测频数和理论频数;Percentages中勾选Row,输出每组转归百分比→Continue→OK
四、结果解读
表2 统计汇总
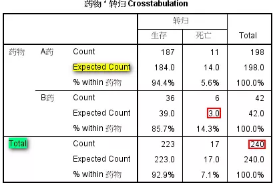
表2中不仅有服用两种药物后患者实际转归(生存/死亡)的频数和相应百分比,还输出了相应的理论频数(所在行列合计数乘积/总例数)。需要注意的是,这里的理论频数和总例数直接决定了下面卡方检验结果的选择。
表3 卡方检验结果
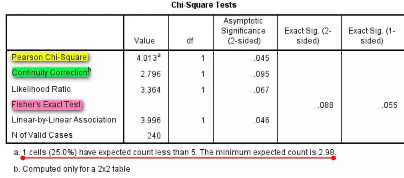
表3中这么多检验结果,到底看哪一个?不要着急 ,我们一个一个来看:
1、总例数≥40,所有理论频数≥5,看Pearson Chi-Square结果;
2、总例数≥40,出现1个理论频数≥1且<5,χ2检验需进行连续性校正,这时以Continuity Correction结果为准;
3、总例数≥40,至少2个理论频数≥1且<5,看Fisher’s Exact Test结果;
4、总例数<40或者出现理论频数<1,看Fisher’s Exact Test结果。
( SPSS也会友好地在表格下方的注释部分提示是否有理论频数小于5,以及最小的理论频数是多少,方便选择恰当的检验方法)
本例中总例数=240>40,存在1个理论频数=3.0<5,所以需要看Continuity Correction结果,χ2=2.796,P=0.095>0.05。
五、撰写结论
两种药物治疗急性心肌梗塞患者的预后并不相同,A药病死率为5.6%,低于 B药(14.3%),但差异无统计学意义(χ2=2.796,P=0.095)。
六、延伸阅读
1、χ2检验是基于χ2分布的一种假设检验,简单讲就是想看看实际观测数和理论频数偏离程度。比如说,上面提到的例子中服用A药后共观察到187例存活,这里的187例就是“实际观测数”,对应的“理论频数”是187所在行列合计的乘积与总例数的比值,也就是198*223/240=184。所有单元格的实际观测数和理论频数计算出后,可根据如下公式计算χ2,得到相应的P值。
χ2=∑[(实际观测数-理论频数)2/理论频数],ν=(行数-1)*(列数-1)
χ2检验的原假设是实际观测数和理论频数分布一致,如果P<0.05,那么拒绝原假设,认为实际观测数和理论频数分布是不一致的,也就是A药和B药治疗后的转归是不同的。当然有了统计分析软件,我们就不需要这么辛苦的计算啦。数据分析培训
2、如果χ2检验所得P值在0.05左右,或者总例数较小,理论频数较少时,给出的结论一定要谨慎,不要简单给出P>0.05或者P<0.05,靠谱儿的做法是给出明确的P值。另外,利用列联表χ2检验比较不同患者某种治疗结局有无差别时,还应该评估不同组患者是否“同质”。举个例子,患者病情严重程度是否一致,这些特征都可能会影响最终结果的判断,对于这一类问题,可以考虑分层χ2检验,logistic回归进行处理,这些后面我们接着聊~~~


