重复测量设计,即对一组或多组受试对象,在k个(k≥2)不同的时间点上,从每个人体(或样本)上重复观测同一个指标的具体取值的设计。如临床研究中,需要观察患者在不同时间的某些生理、生化或病理指标的变化趋势,或治疗干预后不同时间或疗程的疗效特点,就要进行重复测量设计。重复测量数据间存在相关性,不符合方差分析要求,所以重复测量数据资料需要采用专门的统计分析方法,该方法也是近代统计学研究的热点之一。
对于重复测量数据(临床上常称纵向监测数据),实质上每个受试对象的观察结果是多次重复测量结果的连线,统计分析的目的是比较这些连线变化趋势的特征。重复测量试验数据的方差分析需要考虑两个因素,一是处理分组,二是测量时间。可采用的统计分析方法:1. 多元方差分析方法;2. 重复测量数据的方差分析。
重复测量数据的变异由两大部分组成。一是观察对象间差异,二是重复测量间差异。观察对象间差异包括处理组间差异和观察对象个体间变异两部分;重复测量间差异包括测量时间之间差异、处理与测量时间的交互作用和组内误差三个部分。因此,重复测量数据的总变异可分解为处理组、测量时间、处理组与测量时间的交互作用、观察对象间随机误差以及重复测量误差等五个部分。
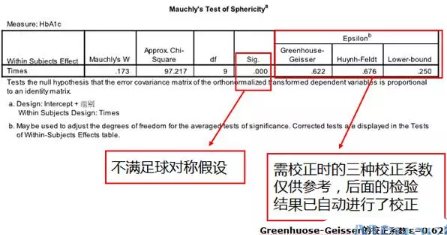
重复测量资料统计前提条件是首先要求样本是随机的,除了满足一般方差分析条件外,特别强调满足协方差阵球形性——球形检验。球形检验(Mauchly):如果P值大于α (如果α=0.05,即p>0.05),说明协方差阵的球对称性质得到满足。若球对称性得不到满足,方差分析的F值是有偏的,会增大Ⅰ类错误的概率,则需校正。否则,必须对与时间有关的F统计量的分子和分母自由度进行调整,减少Ⅰ类错误的概率。调整系数为:ε(epsilon)。
SPSS操作示例
SPSS: Analyze » General Linear Model » Repeated Measures
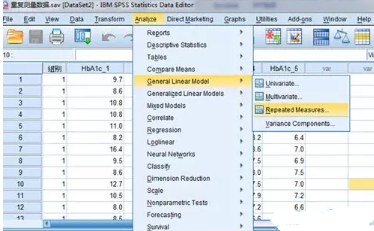
选择重复测量方法
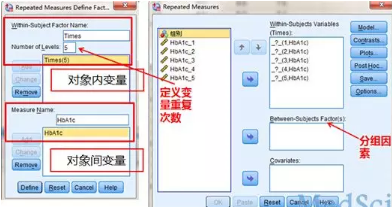
指定对应的测量值
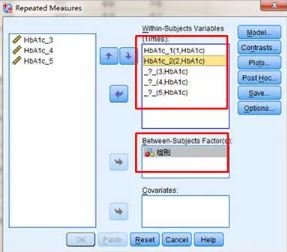
选择Post Hoc
选择Model
选择Option
五次重复测量量的变量名

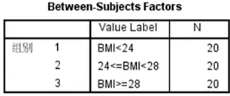
分组变量情况
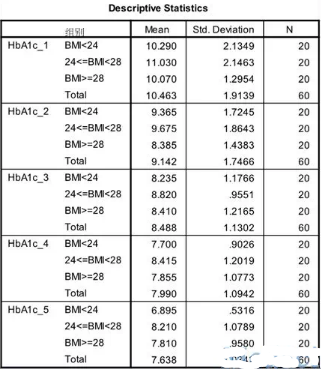
各组各个时间点的详细数据描述
结果解读与展示
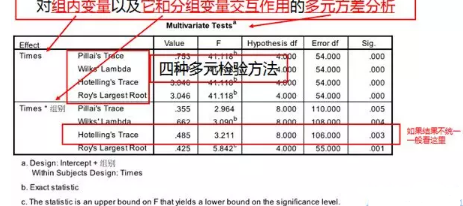
注:各个时间点存在性差异,而且与组别交互中,也存在显著性差异。
球形检验结果
组内因素一元方差分析检验结果
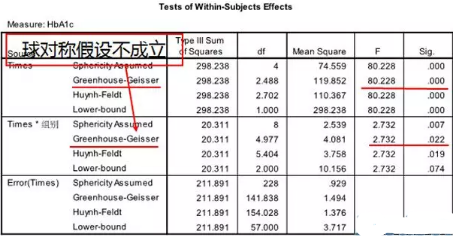
注:不同时间点存在显著性差异,不同组别对各个时间点的结果存在影响。
各重复测量间变化趋势的分析
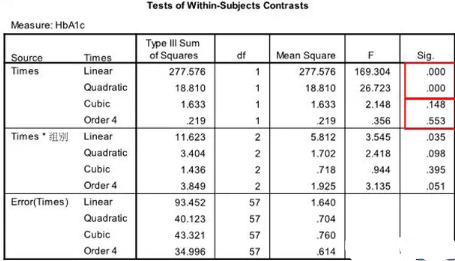
注:不满足线形和二次方趋势;勉强拟合三次或四次曲线,但仅5次测量,要慎重采用。
组间效应的方法分析结果
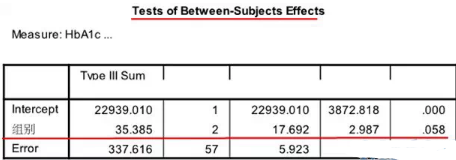
注:组间比较无显著性差异。
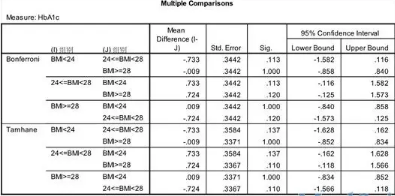
两两比较结果
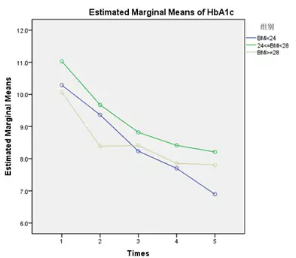
五次测量的均数图
结果
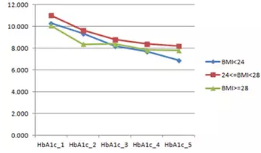
结论:该治疗方法对三组糖尿病患者的糖化血红蛋白的降低无明显差异。
重复测量数据采用一般线性模型(GLM)方法进行测量,这是使用极为广泛的方法。不仅能做多个因素,多个水平的统计,还能控制协变量,从而得出更可靠的结果。甚至临床上多组之间比较,也更倾向采用GLM,而不是ANOVA方法。
虽然GLM的统计理论很复杂,但是作为临床医生更重要的是识别统计方法,合理应用,以及合理解读结果即可,不必吃透复杂的统计原理。重复测量数据采用一般线性模型(GLM)方法,今后运用会越来越广泛,值得大家重视。


