在回归分析中,只有一个自变量的回归分析,称为一元回归;多于一个自变量的回归分析,称为多元回归。在做线性回归分析之前需要先做散点图,如果散点图不呈现线性关系,则不能做线性回归。
一、问题与数据
某地方病研究所调查了8名正常儿童的尿肌酐含量(mmol/24h),请估计尿肌酐含量(Y)对其年龄(X)的直线回归方程。

二、SPSS操作
1、数据录入SPSS。
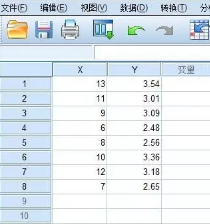
2、做散点图,判断是否是线性关系。
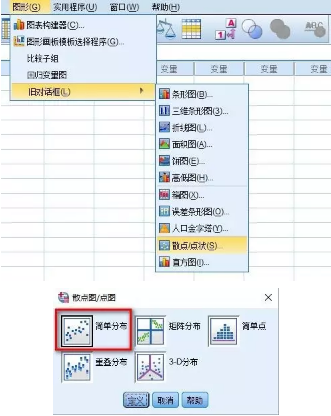
3、将自变量年龄(X)放入X轴;将因变量尿肌酐含量(Y)放入Y轴;其它默认选项后,点击确定。
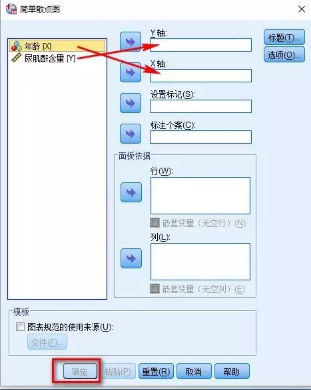
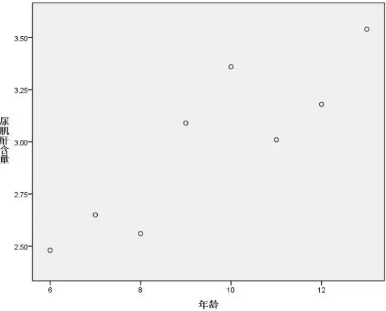
4、从图上判断变量之间大致呈线性关系,可以继续做回归。数据分析培训
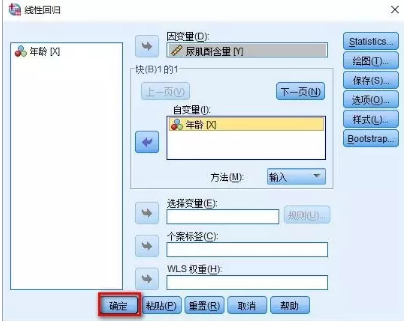
5、将年龄放入自变量,尿肌酐含量放入因变量,点击确定。
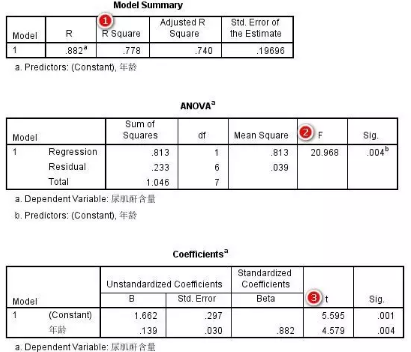
6、结果分析
三、结果解读
①R方(0.778)是回归方程的决定系数,表示Y变异的77.8%可以由X的变异来解释。
②对回归方程进行方差分析:F=20.968,P=0.004。可以认为年龄和尿肌酐含量有直线关系。
③对回归系数进行t检验:Constant(回归方程的截距)与0之间的差别有统计学意义(t=5.595,P=0.001),斜率与0之间的差别有统计学意义(t=4.579,P=0.004)。
因此,建立回归方程为=1.662 0.139X,X为儿童年龄,Y为尿肌酐含量。


