在实际问题中,首先碰到的问题是如何确定自变量。通常是根据所研究的问题,结合经济理论,罗列出对因变量可能有影响的一些因素作为自变量。
因此,我们需要挑选出对因变量有显著影响的自变量,构造最优的回归方程。
逐步回归的基本思想是:将变量一个一个引入,每引入一个变量时,要对已选入的变量进行逐个检验。当原引入的变量由于后面变量的引入而变得不再显著时,将其剔除。这个过程反复进行,直到既无显著的变量选入方程,也无不显著自变量从回归方程中剔除为止。
SPSS应用
步骤:分析->回归->线性,选入需要分析的变量,方法栏中选入“逐步”,如图:
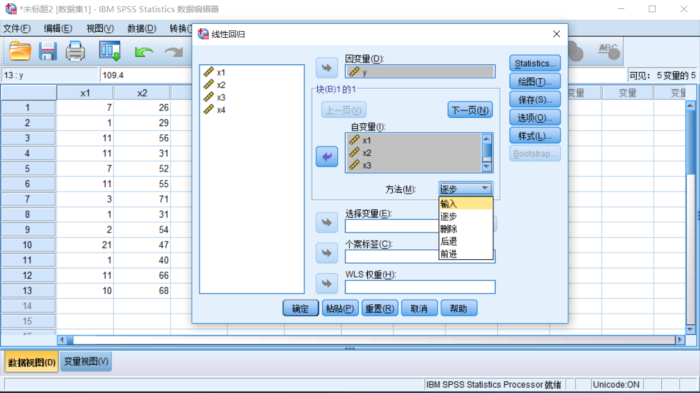
线性对话框
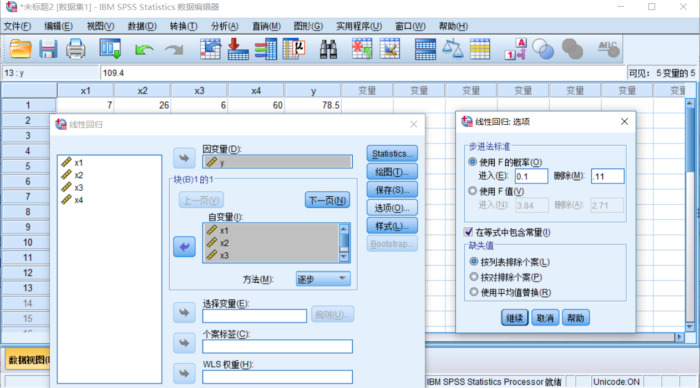
单击选项按钮,在“使用F的概率”中的进入输入0.1,删除输入0.11,如图:
选项对话框
表示当候选变量中最大F值的P值小于或等于0.1时,引入相关变量。在引入方程的变量中,最小F值的P值大于或等于0.1时,则剔除该变量。
输出结果:

表六. 输入或剔除的变量
表六显示变量逐步回归的过程。首先引入了变量x4,建立了模型1;再引入变量x1,建立模型2;引入变量x2,建立模型3;剔除x4,建立模型4。最终建立的模型只包含x1,x2。
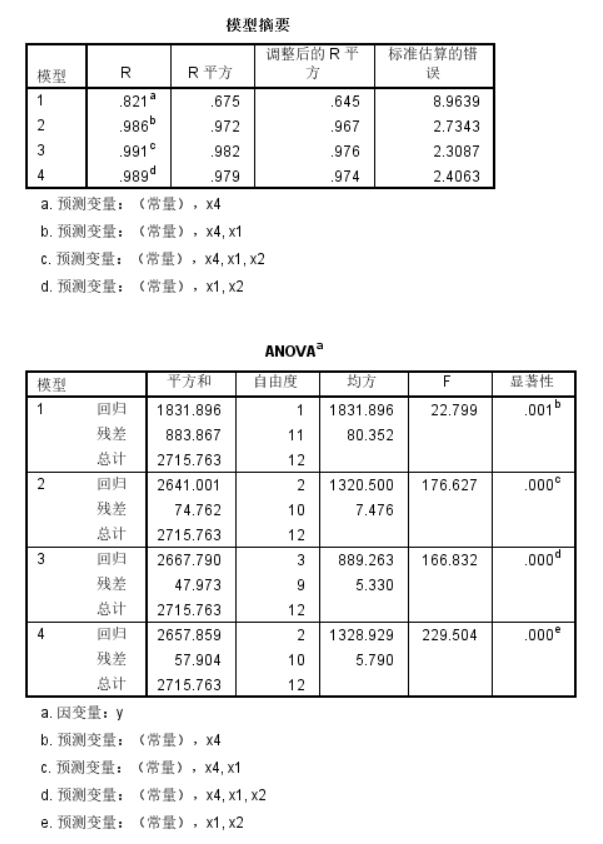
表七、表八. 相关系数和方差
表七和表八主要说明了各模型的拟合情况。模型4的负相关系数为0.989;回归的显著性检验sig=0.00<0.05,说明回归程度显著。
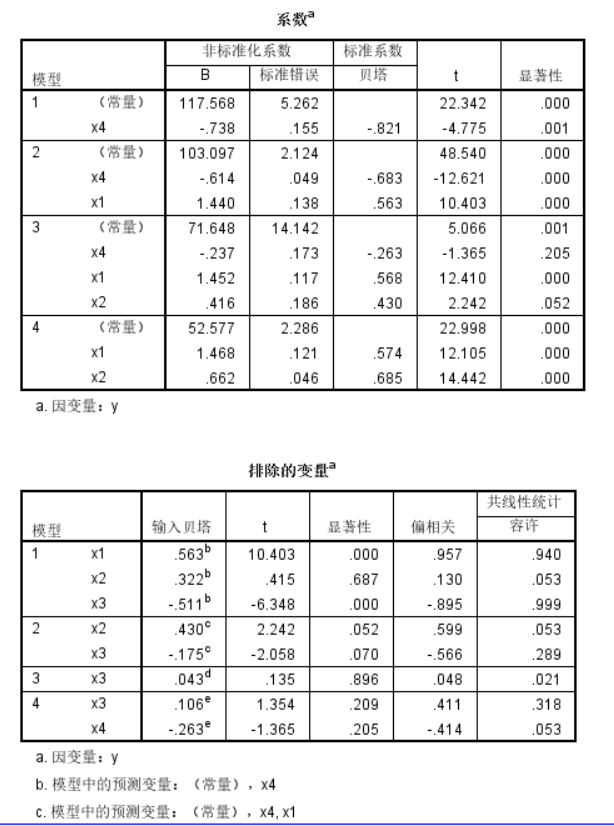
表九、表十. 回归结果
表九给出了回归系数的结果。模型四最后的回归方程为:
表十显示各模型方程外变量的相关统计量。我们可以看到,正是由于x3、x4的P值都大于0.1,所以不能引入模型。


