
文章结构
回归分析是通过建立统计模型研究变量间相关关系的密切程度、结构状态、模型预测的一种有效工具。
一元线性回归分析
一元线性回归是描述两个变量之间统计关系的最简单的回归模型。
1.数学模型

2.估计参数(最小二乘法)

3.方程的显著性检验
求得回归方程后,还不能马上就用它去做分析和预测,还需要应用统计方法对回归方程进行显著性的检验,常用的一般是F检验,其假设及检验统计量见SPSS与方差分析(F检验)
4.SPSS应用
步骤:分析->回归->线性,选入需要分析的变量,方法采用默认的“进入”,如图:
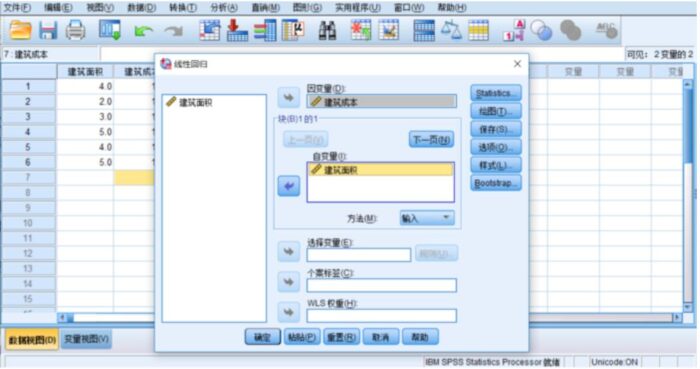
线性对话框
单击Statistics按钮,选择“误差条形图的表征”,选取默认的95%可信区间;“描述性”;“个案诊断”,如图:

Statistics对话框
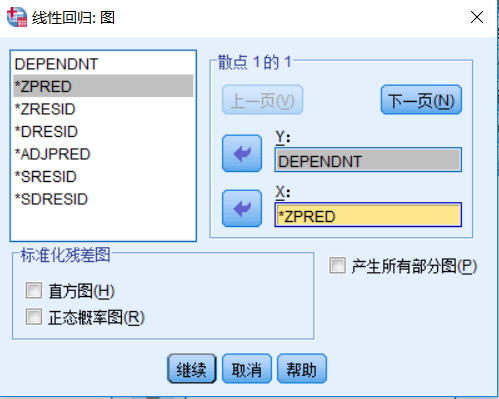
单击绘图按钮,做散点图,选择“DEPENDNT”为Y轴,“*ZPRED”为X轴变量。如图:
绘图对话框
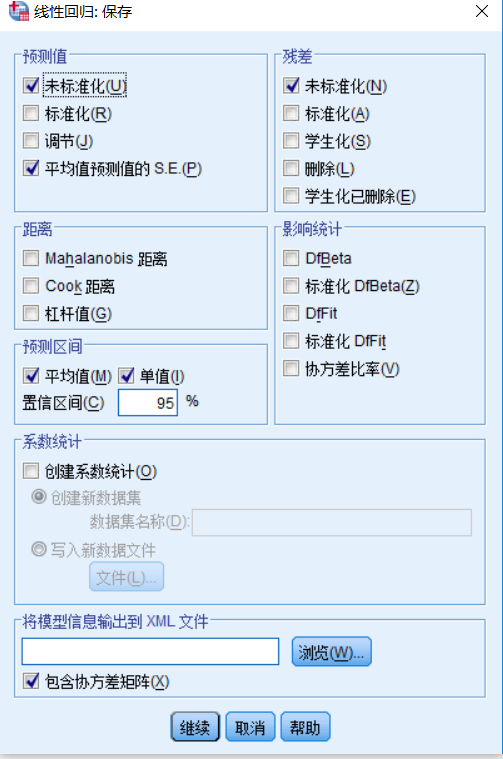
单击保存按钮,选择保存的新变量如下图:
Save对话框
输出结果:
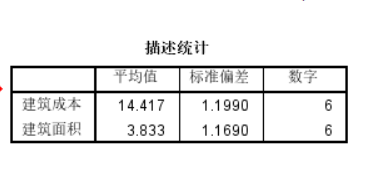
描述性统计量
表一显示x和y的描述统计量。包含均数、标准差和例数。
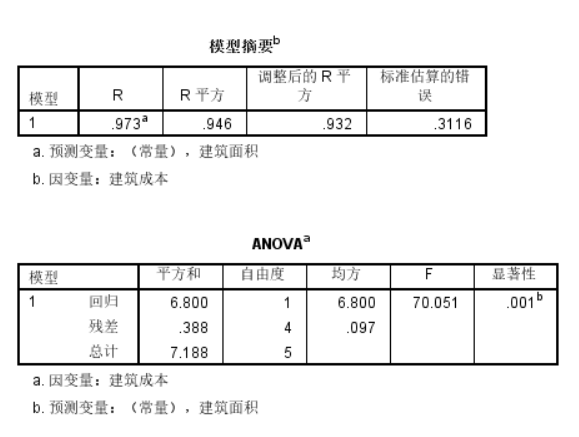
模型摘要和方差分析
表二给出了x和y的相关系数R=0.973,调整后R=0.932。
表三是方差分析结果,回归的均方为6.800,P=0.001<0.05,说明线性回归方程显著。
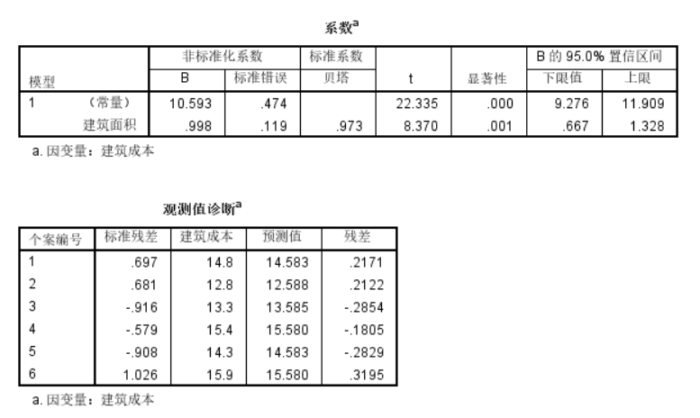
回归系数结果和回归诊断结果
表四是回归系数结果,常数项是10.593,回归系数=0.998,回归系数t检验的P=0.01<0.05,认为回归系数显著有意义。
表五是对全部观测结果进行回归诊断结果。显示每一列样本的标准化残差、因变量y的实测值和预测值。
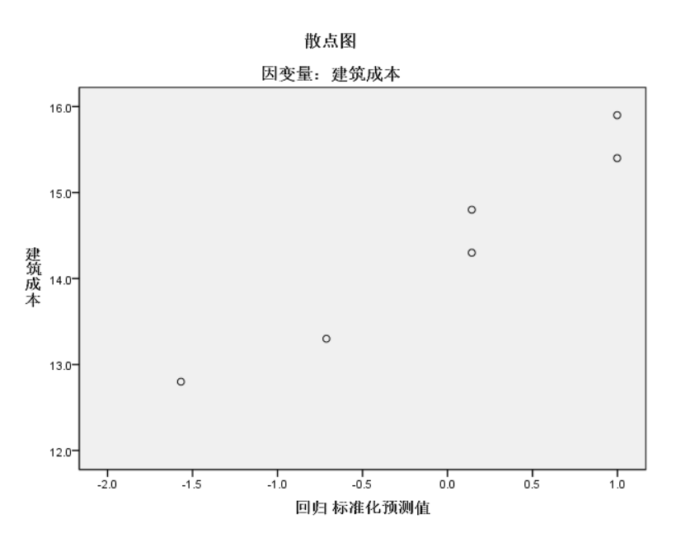
散点图
上图是根据样本点所画的散点图。
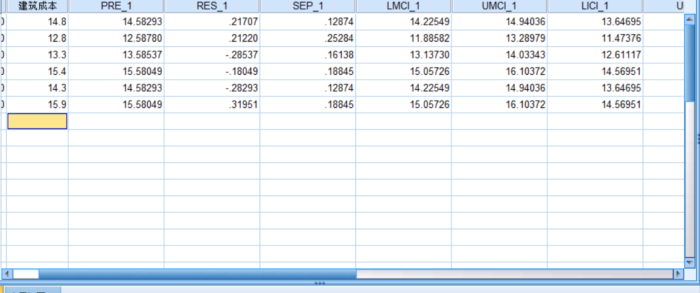
Save命令增加的变量
上图是Save命令的结果,增加的新变量存储在数据窗口中。
多元线性回归分析
多元线性回归分析意味着有多个自变量,其数学模型假设为:
![]()
其它性质及显著性检验可参考一元线性回归分析推断。同样在SPSS应用中,只需选入多个自变量即可,此处不再赘述。


