实质上是将多个指标综合成少数几个指标的方法。
主成分分析是利用降维的方法,在确保数据信息损失最小的原则下,把多个指标转化为少数几个综合指标的一种对多变量数据进行最佳综合简化的多元统计方法。
主成分是原始变量之间的线性组合,且主成分之间互不相关。
主成份分析的主要目的是压缩指标个数、简化数据,但常常与回归分析、因子分析、聚类分析、判别分析等等套用。
基本步骤 计算相关系数阵,检验待分析的变量是否适合做主成份分析。 根据所研究问题的初始变量的特征判断由协方差阵求主成分,还是由相关阵求主成分。
一般来说,分析中选择的变量具有不同的计量单位,或变量水平差异较大时,应选择基于相关系数矩阵的主成分分析。否则还是选择协方差阵做主成份分析效果更好。(实际情况可以都尝试一下~) 求协方差阵或相关系数阵的特征根及对应标准化特征向量。 确定主成分个数。 写出主成分的表达式。 SPSS应用
步骤:分析->降维->因子分析,选入变量后单击描述,如图:
因子分析及描述对话框
单击抽取后选择“碎石图”,保持默认的相关系数阵不变,如图:
抽取对话框
单击得分中的“显示因子得分系数矩阵”,如图:
得分对话框
输出的主要结果:
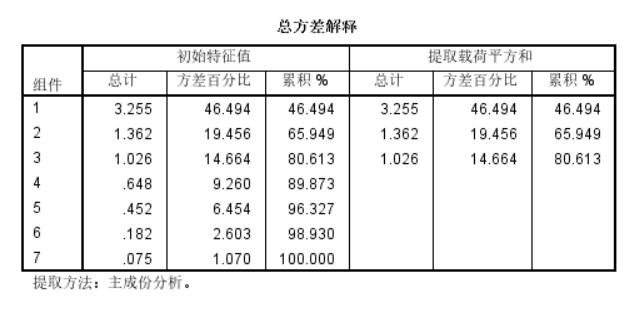
累计贡献率
由表可知,3个主成分可以解释80%左右的总变异。因此选择3个主成分是比较合适的。
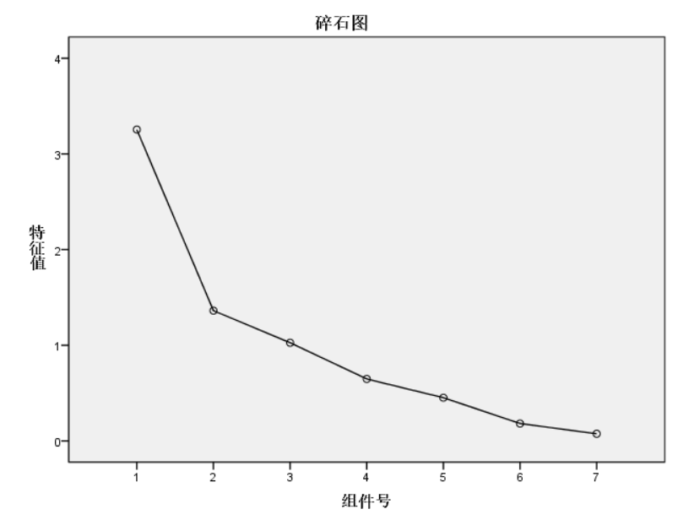
碎石图
碎石图的作用和上表相似。在第3个特征根处趋势变的比较平缓,因此选择三个主成份是合适的。
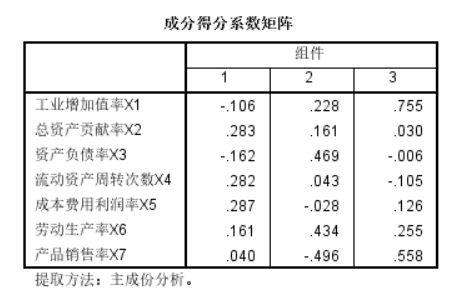
得分系数矩阵
根据得分系数矩阵可以写出标准化的原始变量表示的主成分的表达式。
因子分析 基本思想:
因子分析是主成分分析的推广。
同是在确保数据信息丢失的原则下,因子分析研究变量之间的内部依赖关系,从原始变量的相关矩阵出发,将相关性较强的变量归于一类,最终形成几类假想型变量。每类变量代表了一个“公共因子”(本质因子、基本特征)。
因子分析主要功能是简化数据、探测数据的基本结构。还可以与回归分析、聚类分析、判别分析等套用。
基本步骤 选择分析变量,检验待分析的原始变量是否适合做因子分析。
SPSS提供了3种检验方法判断数据是否适合做因子分析:巴特利特球形检验、反映像相关矩阵检验、KMO检验 提取公因子(默认是主成分分析法)。 选择合适公因子的数量(累计贡献率70%以上)。 旋转因子使公因子具有可解释性。
SPSS提供了多种旋转方法,之所以有这么多方法,是因为没有一种方法令人完全满意。所以在不知道该用哪种方法旋转时,采用默认的方差最大法即可。 进行因子命名。
需要研究者主观分析。可以根据因子载荷较大对应的几个原始变量的含义尝试对因子进行命名。 计算因子得分,进行结果解释。 SPSS应用

步骤:分析->降维->因子分析,选入变量后单击描述,选择KMO和巴特利特球形检验,如图:
描述对话框
输出结果:

检验结果
KMO的值=0.687>0.05勉强可以进行因子分析。巴特利特球形检验的p=0.009<0.05,认为合适进行因子分析。
接下来,重复上节的主成分步骤,得到3个主成分,其累计贡献率为80%左右。
为了更好地解释公因子含义,点击旋转,如图:
旋转对话框
输出的主要结果:
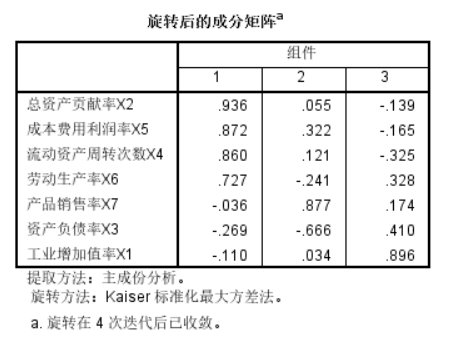
旋转后的成分矩阵
由表可知,因子1在X2、X5、X4上有较大载荷,可命名为资产因子;因子2在X7上有较大载荷,可命名为销售率因子;因子3在X1上有较大载荷,可命名为增加值率因子。
主成分分析 VS 因子分析 基本思想
两者都是处理多变量数据的一种统计方法,都可以达到对数据简化的目的。
但二者又有很大不同。主成分分析仅仅是变量变换,强调解释数据变异的能力,适合做数据简化,模型中没有误差项,主成分没有实际意义;而因子分析是要寻找变量内部的相关性及潜在的公共因子,强调变量之间的相关性,适合检测数据结构,模型中有误差项,公因子一般有实际意义。
基本步骤
因子分析实际上是建立在主成分分析上的,可以看作是主成分的推广和扩展。主成分又可以看作是因子分析的一个特例,是因子分析中因子载荷估计的一种方法。
| 比较 | 主成分分析 | 因子分析 |
|---|---|---|
| 思想 | 通过变量变换把注意力集中在具有较大变差的那些主成分上,而舍弃那些变差小的主成分。 | 因子分析把注意力集中在少数不可观测的潜在变量(即公共因子)上,而舍弃特殊因子。 |
| 系数 | 主成分的各系数,是唯一确定的、正交的。 | 因子分析的系数矩阵是不唯一的、可以进行旋转的。 |
| 核心 | 主成分是各成分之间的线性变换。 | 因子分析的各因子具有确定的解释意义。 |


