推断统计是研究如何利用样本数据来推断总体特征的统计方法。包含两个内容:参数估计,即利用样本信息推断总体特征;
假设检验,即利用样本信息判断对总体的假设是否成立。
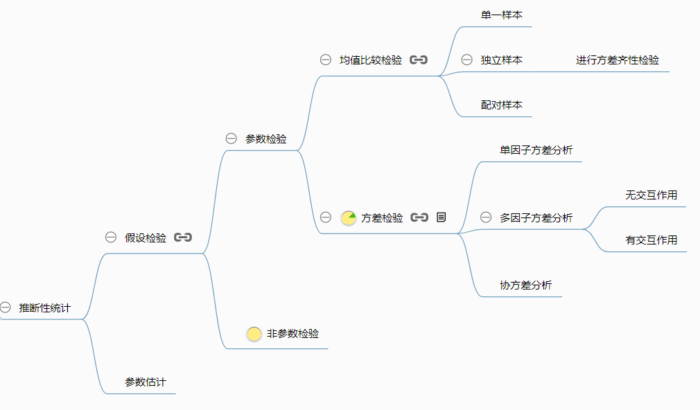
假设检验
正如一个法庭宣告某一判决 为“无罪(not guilty)”而不为“清白 (innocent)”,统计检验的结论也应 为“不拒绝”而不为“接受”。
——Jan Kmenta
因此,假设检验实质是“证伪”的过程。
“假设”实际包含的意义是对总体参数的数值所作的陈述。总体参数包含均值、比例、方差等。
假设检验的标准步骤
1. 建立假设
提出原假设H₀以及对立的备择假设H₁。
原假设是我们“想要推翻”的假设。因此原假设总是包含等号,写成:
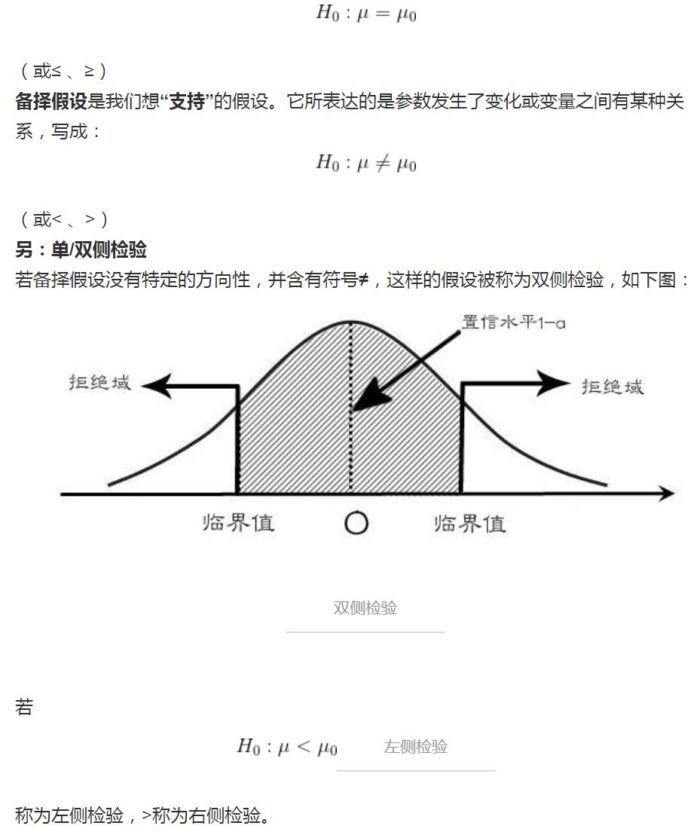
2. 确定检验统计量
假设确立后,要决定接受还是拒绝假设,都是通过构造样本的统计量并计算该统计量的概率值进行推断的。
在统计检验的理论中,针对均值的检验可分为三种:
总体方差σ²已知,不论是大样本(n≥30)或小样本,都可以使用Z值和正态分布处理; 总体方差σ²未知,小样本,应用t值和T分布处理; 总体方差σ²未知,大样本,应用Z值和Z分布处理
由于一般的统计软件都只包含t检验而没有Z检验。所以样本的均值比较检验也称样本的t检验。
3. 确定检验水准
设定显著性水平α,即小概率事件的界值。常选取α=0.01,0.05,0.10
决策是建立在样本信息的基础之上,而样本是随机的,因此有可能出现决策失误,即假设检验的两类错误。
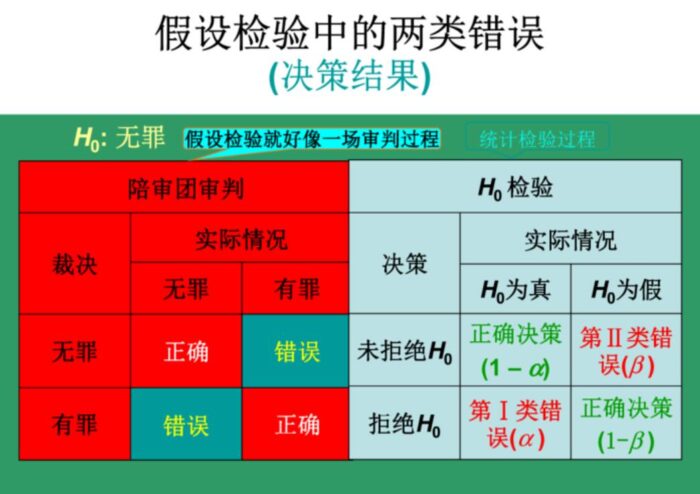
4. 进行试验
得到用于统计分析的样本
5. 计算P值并给出推断结论
P值:就是当原假设为真时所得到的样本观察结果或更极端结果出现的概率。P值越小则越可能发生小概率事件。
决策规则:P<α 则拒绝原假设,P>α 则不拒绝原假设。/或统计量的值落在拒绝域,拒绝H₀,否则不拒绝H₀。
注:P值和统计量是不同的。


