当我们去探讨研究疾病与相关因素之间的关系时,常常因为涉及的相关因素较多,需要去考虑是否存在混杂效应或者是存在变量间的交互作用。但是,如何判断一个变量是混杂因素还是效应修饰因子呢?
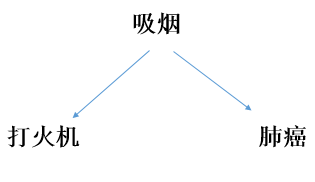
混杂因素是指能同时导致研究因素和研究疾病,若在比较的人群组中分布不均衡,可以夸大或者缩小研究因素与疾病之间真实的联系的因素。例如,当我们研究打火机和肺癌的关系时,是否吸烟就是一个潜在的混杂因素。通过有向无环图我们可以发现,打火机因素可以通过后门通路路径经过吸烟连接到肺癌,若不控制吸烟因素,就会歪曲打火机与肺癌之间真实的因素。
从统计学的角度来看,假设我们先建立一个简单线性回归模型:
E(Y) = β0 β1X1 (1.1)
如果探讨变量X2是否是混杂因素,我们将变量X2作为一个新的自变量带入上面的线性模型:
E(Y) = β0 β1X1 β2X2 (1.2)
当式(1.1)中Y与X1关系的粗估计值β1(没考虑有X2的情况)与式(1.2)中得到的调整β1/X2间有实际意义的不相等(β1 ≠ β1/X2),同时经过研究者的临床专业知识判断后,我们可以有倾向性地认为X2是一个潜在的混杂因素。
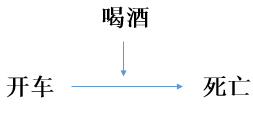
交互作用是指当两个或两个以上因素共同作用于某一事件时,其效应明显不同于该两个或两个以上因素单独作用时的和或积,称因素间存在交互作用。举一个生活中的例子,司机开车可能会增加死亡的风险(发生车祸),而如果司机酗酒后开车,那就会急剧增加死亡的风险,这时我们可以认为开车和喝酒存在交互作用。
从统计学角度来看,我们建立一个仅有两个自变量的线性回归模型:
E(Y) = β0 β1X1 β2X2 β3X1X2 (1.3)
式(1.3)中的乘积项称为交互项。假如没有交互项时,β1表示为X2不变时,X1每改变一个单位,Y的平均改变值;同理,β2表示为X1不变时,X2每改变一个单位,Y的平均改变值。当存在交互项时,我们会发现当X1保存不变,X2每改变一个单位,Y的平均改变值为β2 β3X1;同理,当X2保存不变,X1每改变一个单位,Y的平均改变值为β1 β3X2。
通常,我们会观察效应值β3在模型中是否有统计学意义。若有,则表示某一个变量的效应值大小变化会需要考虑另外一个变量的取值大小,在条件效应图中将会提示两条直线不平行,即斜率不同。
当存在效应修饰因子时,研究因素与疾病之间的效应会发生真实的改变,这是研究者需要尽可能去发现的地方(发paper的关键),它的存在与否与研究设计本身无关。而混杂是可能影响研究真实性的因素,但是可以在研究设计阶段进行预防,以及在统计分析时进行控制。另外,在实际操作过程中,研究者需要先判断某因素是否是混杂因素,再进行是否存在交互作用的判断。


