当我们希望获得研究因素与研究疾病(事件)之间真实关系时,最主要的考虑是校正混杂因素,因为混杂因素的影响,会掩盖或夸大两者之间的真正联系。那我们只考虑校正混杂因素就够了吗?其实,我们还需要避免造成选择偏倚。今天,小编将用有向无环图带大家来初探下其中的秘密。
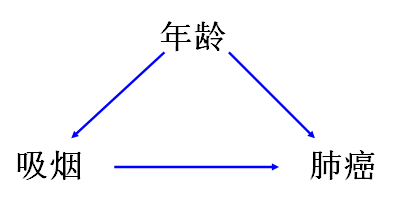
吸烟与肺癌关系的病例对照研究中,假设年龄是唯一的混杂因素,即病例组和对照组间年龄分布不同,同时年龄也是导致肺癌的危险因素。此时,如果研究者想获得吸烟与肺癌之间真正的效应估计值时,我们就需要校正年龄这个因素。
但在实际场景中,我们可能并不知道年龄是一个混杂因素,此时我们通常是通过比较存在该因素时研究因素与疾病(事件)的效应估计值(RR、OR等),与调整了该因素后的效应估计值之间是否有差异(p<0.05或<0.1),来判断是否需要校正该因素。
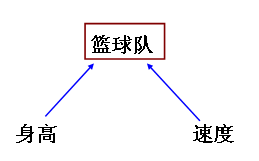
那我们再来看看选择偏倚是怎么产生的。首先,我们先明确身高(自变量)不会影响跑步速度快慢(因变量)。举一个极端的例子,我们需要组建一支篮球队,只有要么个子高要么跑步快的人能加入这个球队。我们会发现在篮球队中,身高和跑步速度呈负相关,因为在篮球队中的任何一个人,不是个子高就肯定是速度快。如果我们仍然是通过比较存在该因素时研究因素与疾病(事件)的效应估计值(RR、OR等),与调整了该因素后的效应估计值之间是否有差异(p<0.05或<0.1),来判断是否需要校正该因素,我们可能会想当然的去调整篮球队这个因素,从而错误地估计身高与速度之间的真实关系。这是因为混杂和选择偏倚从流行病学的角度上来看是完全不同的两个概念,但是从统计学的表达形式上看却是相同的。
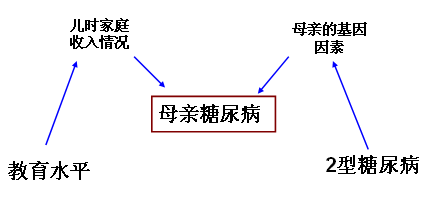
再来举个例子,假如我们想探讨研究对象的教育水平(自变量)和是否患2型糖尿病(因变量)之间的真实联系,研究者收集到的研究因素包括教育水平、
患2型糖尿病情况以及研究对象的母亲患2型糖尿病情况。那我们是否需要调整母亲患糖尿病情况呢?如果按照上述统计的辨别方式,我们显然需要调整该因素,但是通过有向无环图显示(儿时的家庭收入情况和母亲的基因因素是该研究未测量指标),其实这只是我们产生的选择偏倚,如果调整了该因素,就会错误地估计教育水平和2型糖尿病之间的联系。