可是,正确率(Accuracy)呢?我们来看个例子:
假设诊断试验纳入了200名研究对象,sen=0.8,spe=0.9,研究对象中患病比例是50%,我们可以得到以下四格表:
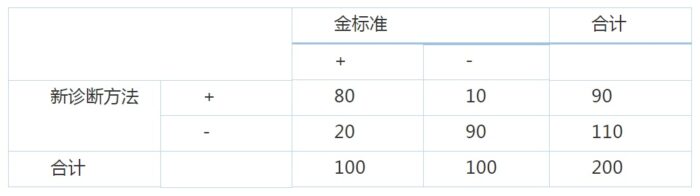
正确率(Accuracy)=(80 90)/200=0.85
而如果患病比例是75%呢?
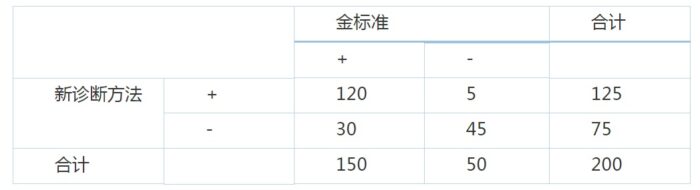
正确率(Accuracy)=(120 45)/200=0.825
而如果患病比例是25%呢?
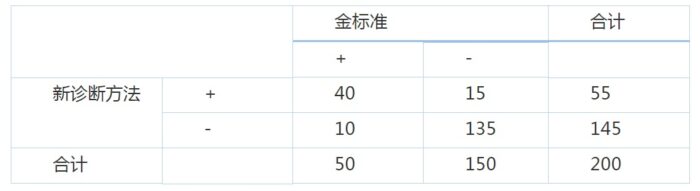
正确率(Accuracy)=(40 135)/200=0.875
从上面这个例子看来,似乎正确率和患病比例是有关系的啊。同样的灵敏度和特异度条件下,当患病比例为50%时,正确率是0.85,当患病比例提高到75%时,正确率是0.825,而当患病比例下降到25%时,正确率则等于0.875。那是不是随着患病比例的降低,正确率会升高,两者是负相关呢?一个例子并不足以总结普遍规律,下面我们来探索一下正确率和患病比例间的数量关系。
首先我们要构建一个通用的四格表,如下:
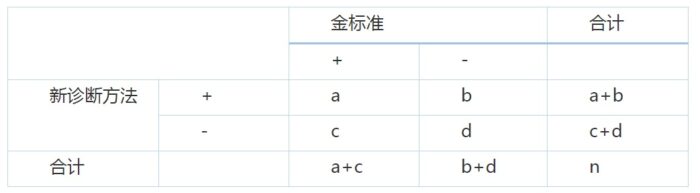
那么灵敏度、特异度、患病率和正确率分别如下:
Sen=a/(a c)Spe=d/(c d)
Prevalence=(a c)/n
Accuracy=(a d)/n
我们把Accuracy展开就可以得到以下公式:

从上面这个推导的公式可以看到,当灵敏度>特异度时,正确率随着研究人群患病比例的增加而增加,当灵敏度<特异度时,正确率则会随着研究人群患病比例的增加而减少,有趣的是,当出现灵敏度=特异度时,正确率与患病比例无关。
还是用上面的例子来验证一下,如果灵敏度=0.9,特异度=0.8,即Sen>Spe则结果如下:
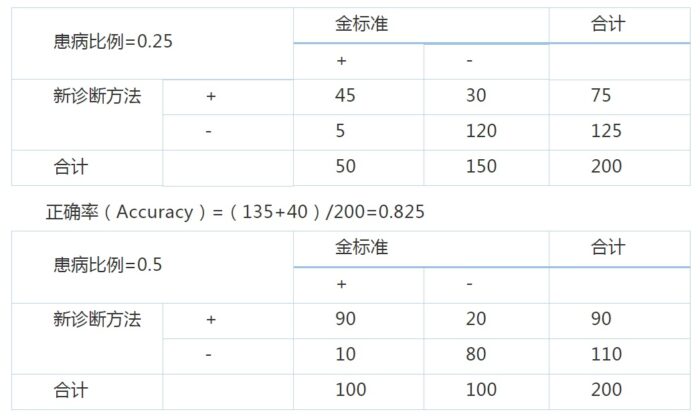
正确率(Accuracy)=(80 90)/200=0.85
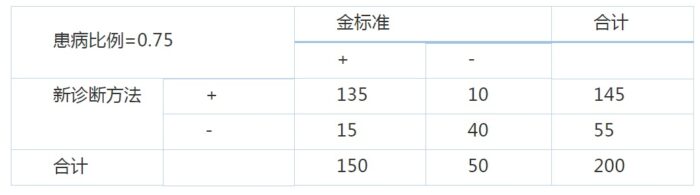
正确率(Accuracy)=(135 40)/200=0.875
可见正确率是随着患病比例的增加而上升的。最后剩下Sen=Spe的情况,请大家自行用数据来脑补一下喽。
当我们以后评价诊断方法的综合效果时,正确率(Accuracy)是很常见的一个指标,但是别忘记这个指标在大叔多情况下还是和人群的患病率有关,也就是说,如果在文献中读到某种新诊断方法正确率的时候一定要考虑这个研究的人群和我们要应用这种诊断方法人群的关系,当患病率不等的时候,往往不能重复出原来的正确率哦。


