最简单的因果关系无非只有两头,一头是因,另一头是果:

上图就是最简单的因果关系,X是原因,Y是结果,这想必大家都能理解。而c和e又是什么呢?c其实是X对Y效应的大小,比如我们建立回归模型时的“系数”就是最典型的c。同样在这一因果关系中,X和c共同解释了Y的一部分变化(当然可多可少),但是如上所述,毕竟无法解释所有Y的变化。那么e就出现了,我们把Y的变化中所有没能被原因X所解释的部分通通丢给e,所以e到底是什么?我们也说不清楚,在统计学上我们统一把它称为残差。
二、我们还算熟悉的因果关系
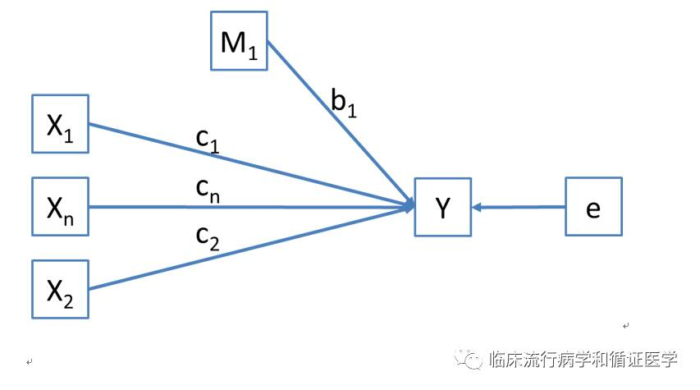
正如单因素和多因素分析的差别一样,对于某个结局Y,通常也不会只有一个原因X,可能对应了多个原因共同对Y产生作用,当然这些原因之间也许还存在复杂的关联和相互影响,甚至其中一个X会影响另一个X对Y发挥的作用,这些我们暂且不表,毕竟不是本篇文章关注的重点。在众多X中还混入了一个M,单独看上去似乎也是Y的一个原因。
三、我来搅浑水
更一般的情况也许是这样的,M本身是不是Y的原因并不清楚,至少看起来M与Y的改变息息相关。但是我们能够清楚的是X1是M的原因。大家混乱的关系变成了下面这个样子:
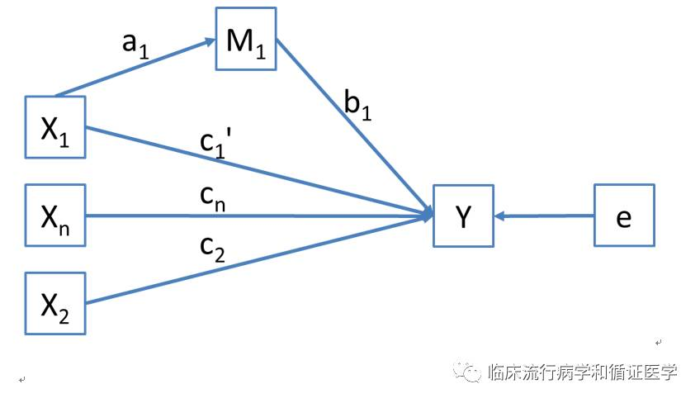
各种X是Y的原因,这个观点无需多说了,毕竟从图看,每一个X都有一条线指向Y。但是同时X1是M1的原因,M1又是Y的原因。如果红色部分成立的话,M1就成了X1和Y之间的中间变量,此时M1产生的效应为中介效应。也就是说,X1表现出来对Y的影响,至少有一部分(或者全部)是通过改变M1带来的。
四、中间变量/中介效应好吃么?
1、有助于我们了解机制,也许可以作为潜在的干预点。
如果有其他因素也能对M1带来相同的改变,那么必然也会对Y带来相同的影(等同于通过M1带来的影响)。同样,如果改变X1之后,我们组织了M1的改变,那么对应的变化也不会发生在Y身上。这就是中间变量和中介效应的奇妙之处,如果我们发现了中间变量和中介效应,那么我们其实就向真理又迈进了一步。即便不会为临床带来什么实际产出,至少也有利于我们从临床向基础的转化。
2、可以作为结局的预测/预警指标
如果中间变量先于结局出现,同时中间变量的状态可被我们观察或测量到,那么中间变量最直接的作用就是能让我们更早的预计结局Y的发生。基于中间变量的预测,比基于早期指标X的预测可能靠谱的多。
五、如何证明中间变量/中介效应的存在?
其实上面已经给出图了,图中各种a、b、c是否有统计学意义,其实就决定了中介效应是否存在。
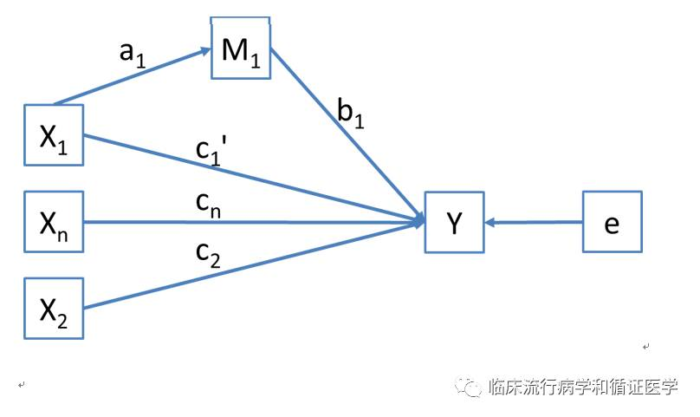
在图中,我们探索中介效应的方式其实并不难,就是通过我们常用的各种多因素回归模型。我们需要做的就是分步骤把对应的Y、X和M代入模型,然后观察对应的系数是否有统计学意义,具体步骤如下。
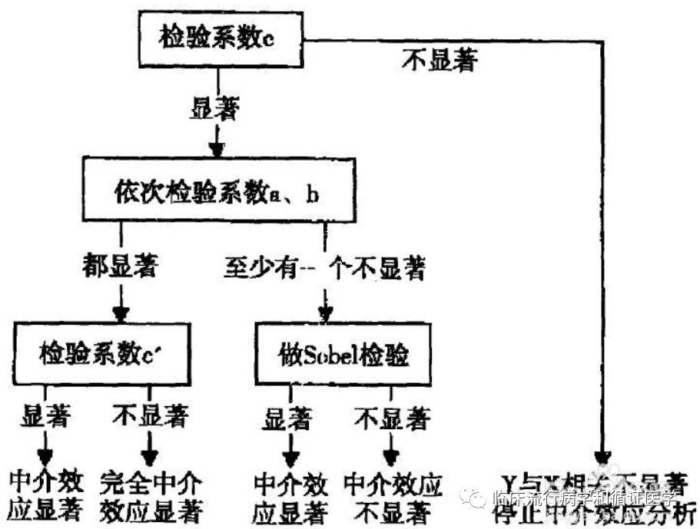
其中所谓的“完全中介效应”是指X对Y的所有效应实际上都是通过改变M带来的,这是一种较为极端的情况。更常见的情况是,X的一部分效应是通过M来实现的。


