随着收集数据的成本降低,数据的量越来越大。关于每个病例或者样本,我们可收集很多指标。但对于应实践应用,不是指标越多越好,而越少越简单越好。如果能用一个指标代替的数据,就最好不要用多个指标进行描述,因为前者应用时要求指标简单、意义明确。因此在大数据时代数据需要降维。主成分分析就是其中一种降维的方法。
主成分分析(Principal ComponentAnalysis,PCA)一种数据降维技术,将多个具有较强相关性的实测变量综合成少量综合变量。其原理也比较简单,首先需要我们理解变异的重要性。在数据中,一个指标除了可靠、真实之外,还必须反映个体间差异。数据的变异是数据信息的承载体,不同个体取值大同小异,该指标不能很好的区分个体,变异越大,信息量越大。举个极端的例子,如果一个研究中性别会为“女”,身高全为170cm,那这两个变量在本研究中就是恒量,在主成分分析中认为这两个变量没有提供信息。比如下面一个散点图的数据,假设两个指标的单位相同,X轴代表的参数信息量要大于Y轴代表的参数信息量。
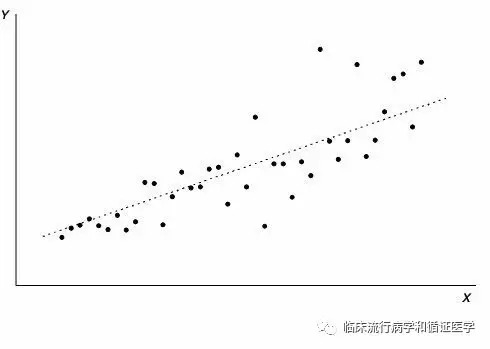
对于下面一个数据,X轴和Y轴的信息量差不多,我们是否可以数据的变异集中在一个变量上呢?
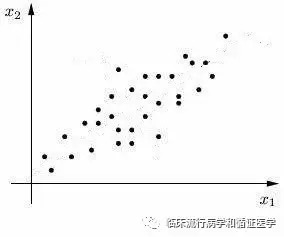
如果我们旋转和移动坐标轴之后,用新坐标体系表示数据,
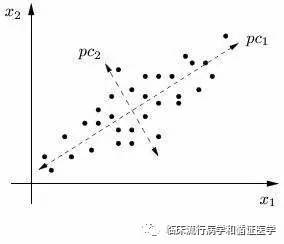
PC1代表的信息量要远大于PC2的信息量,此时PC2的信息量可忽略,即我们用PC1一个变量代替原来X、Y两个,即达到的降维的目的。两个原始变量对应二维空间,这种变换我们很容易理解。原始变量个数对应了空间维数,我们做的主成分分析往往有多个变量,高维空间与二维和三维空间相类似,都是通过空间旋转和平移后得到。
从上面图中也很比较容易得到,主成分分析应用于两个或多个变量高度相关的情况,如果各变量间不相关或相关性较弱,主成分分析得不到较理想的结果。
理解了主成分分析的原理,有助于我们做主成分分析结果的解读。与主成分相关的另外一种统计方法是因子分析,我们下次再解析。


